
Question Number 68676 by Rio Michael last updated on 14/Sep/19

$${Solve}\:{the}\:{equation} \\ $$$${tanh}^{−\mathrm{1}} \left(\frac{{x}−\mathrm{2}}{{x}+\mathrm{1}}\right)\:=\:{ln}\:\mathrm{2} \\ $$$${show}\:{that}\:{the}\:{set}\:\left\{\mathrm{1},\mathrm{2},\mathrm{4},\mathrm{8}\right\}\:\:{under}\:×_{\mathrm{15}} \:,{multiplication}\:{mod}\:\mathrm{15}\:\:{forms}\:{a}\:{group}. \\ $$
Commented by MJS last updated on 14/Sep/19
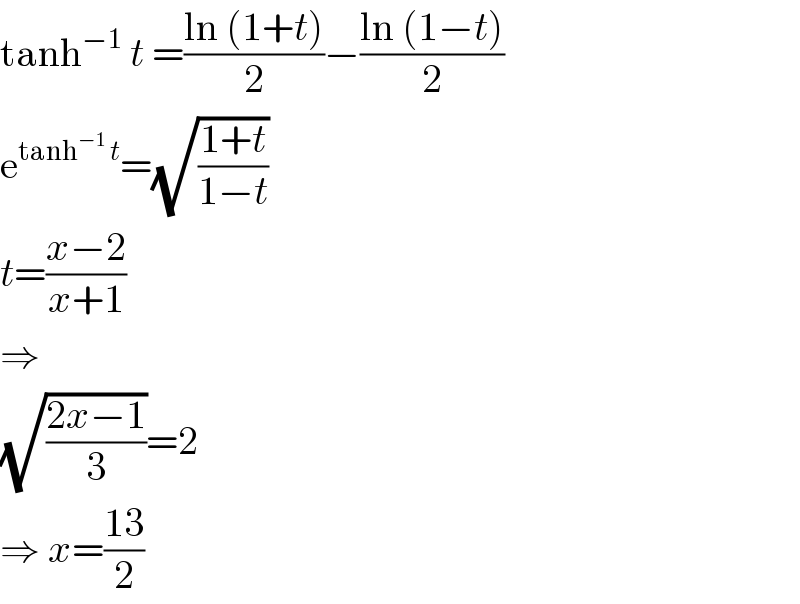
$$\mathrm{tanh}^{−\mathrm{1}} \:{t}\:=\frac{\mathrm{ln}\:\left(\mathrm{1}+{t}\right)}{\mathrm{2}}−\frac{\mathrm{ln}\:\left(\mathrm{1}−{t}\right)}{\mathrm{2}} \\ $$$$\mathrm{e}^{\mathrm{tanh}^{−\mathrm{1}} \:{t}} =\sqrt{\frac{\mathrm{1}+{t}}{\mathrm{1}−{t}}} \\ $$$${t}=\frac{{x}−\mathrm{2}}{{x}+\mathrm{1}} \\ $$$$\Rightarrow \\ $$$$\sqrt{\frac{\mathrm{2}{x}−\mathrm{1}}{\mathrm{3}}}=\mathrm{2} \\ $$$$\Rightarrow\:{x}=\frac{\mathrm{13}}{\mathrm{2}} \\ $$
Commented by Rio Michael last updated on 15/Sep/19

$${thank}\:{you}\:{sir} \\ $$
