
Question Number 155244 by mathdanisur last updated on 27/Sep/21
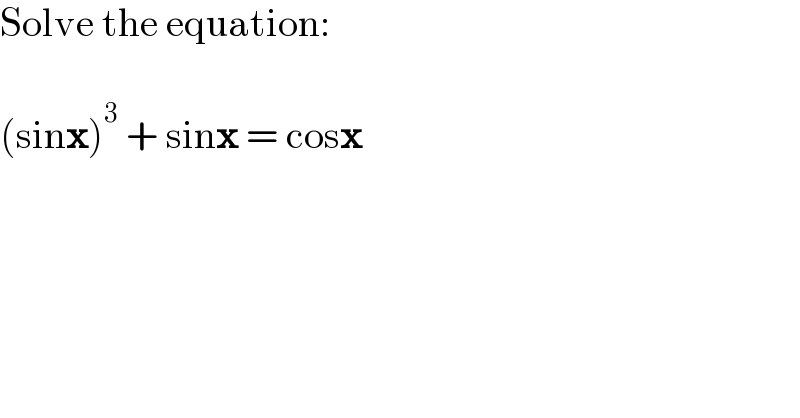
$$\mathrm{Solve}\:\mathrm{the}\:\mathrm{equation}: \\ $$$$ \\ $$$$\left(\mathrm{sin}\boldsymbol{\mathrm{x}}\right)^{\mathrm{3}} \:+\:\mathrm{sin}\boldsymbol{\mathrm{x}}\:=\:\mathrm{cos}\boldsymbol{\mathrm{x}} \\ $$
Answered by ajfour last updated on 27/Sep/21
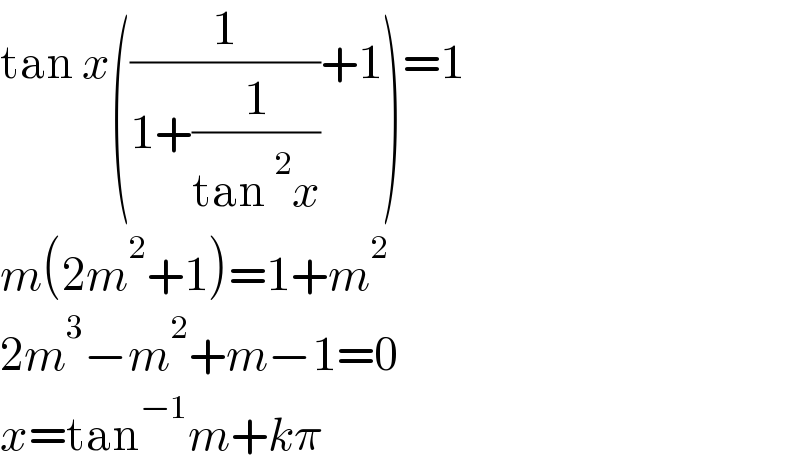
$$\mathrm{tan}\:{x}\left(\frac{\mathrm{1}}{\mathrm{1}+\frac{\mathrm{1}}{\mathrm{tan}\:^{\mathrm{2}} {x}}}+\mathrm{1}\right)=\mathrm{1} \\ $$$${m}\left(\mathrm{2}{m}^{\mathrm{2}} +\mathrm{1}\right)=\mathrm{1}+{m}^{\mathrm{2}} \\ $$$$\mathrm{2}{m}^{\mathrm{3}} −{m}^{\mathrm{2}} +{m}−\mathrm{1}=\mathrm{0} \\ $$$${x}=\mathrm{tan}^{−\mathrm{1}} {m}+{k}\pi \\ $$
Commented by mathdanisur last updated on 27/Sep/21
$$\mathrm{very}\:\mathrm{nice}\:\boldsymbol{\mathrm{S}}\mathrm{er},\:\mathrm{thank}\:\mathrm{you} \\ $$
Commented by mathdanisur last updated on 27/Sep/21
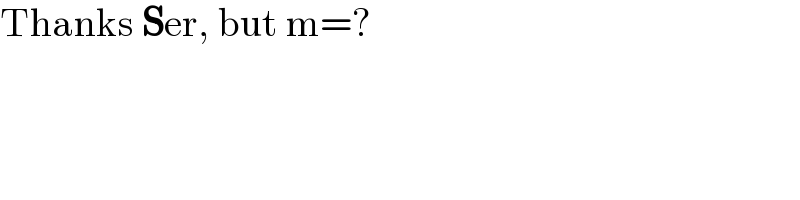
$$\mathrm{Thanks}\:\boldsymbol{\mathrm{S}}\mathrm{er},\:\mathrm{but}\:\mathrm{m}=? \\ $$
Commented by mr W last updated on 27/Sep/21
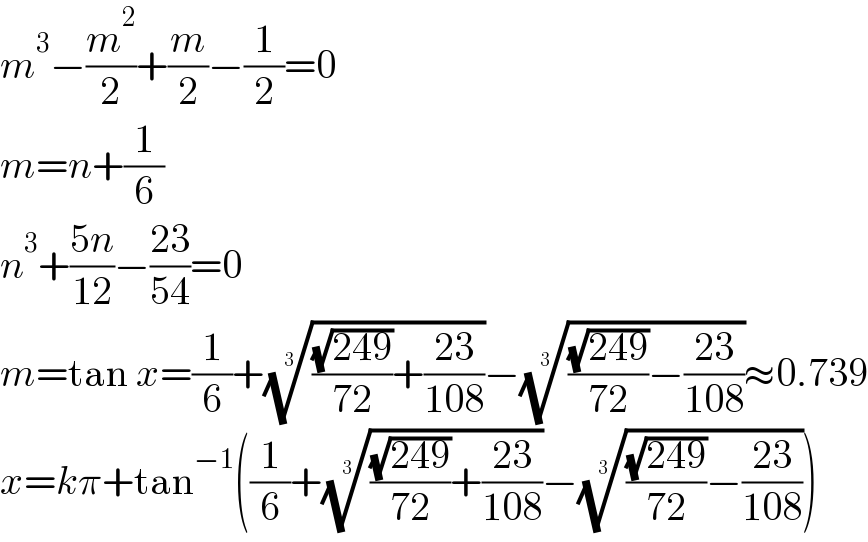
$${m}^{\mathrm{3}} −\frac{{m}^{\mathrm{2}} }{\mathrm{2}}+\frac{{m}}{\mathrm{2}}−\frac{\mathrm{1}}{\mathrm{2}}=\mathrm{0} \\ $$$${m}={n}+\frac{\mathrm{1}}{\mathrm{6}} \\ $$$${n}^{\mathrm{3}} +\frac{\mathrm{5}{n}}{\mathrm{12}}−\frac{\mathrm{23}}{\mathrm{54}}=\mathrm{0} \\ $$$${m}=\mathrm{tan}\:{x}=\frac{\mathrm{1}}{\mathrm{6}}+\sqrt[{\mathrm{3}}]{\frac{\sqrt{\mathrm{249}}}{\mathrm{72}}+\frac{\mathrm{23}}{\mathrm{108}}}−\sqrt[{\mathrm{3}}]{\frac{\sqrt{\mathrm{249}}}{\mathrm{72}}−\frac{\mathrm{23}}{\mathrm{108}}}\approx\mathrm{0}.\mathrm{739} \\ $$$${x}={k}\pi+\mathrm{tan}^{−\mathrm{1}} \left(\frac{\mathrm{1}}{\mathrm{6}}+\sqrt[{\mathrm{3}}]{\frac{\sqrt{\mathrm{249}}}{\mathrm{72}}+\frac{\mathrm{23}}{\mathrm{108}}}−\sqrt[{\mathrm{3}}]{\frac{\sqrt{\mathrm{249}}}{\mathrm{72}}−\frac{\mathrm{23}}{\mathrm{108}}}\right) \\ $$
Answered by MJS_new last updated on 27/Sep/21
![sin^3 x +sin x =cos x sin^3 x +sin x =±(√(1−sin^2 x)) sin x =s s^3 +s=±(√(1+s^2 )) squaring [might introduce false solutions] and transforming s^6 +2s^4 +2s^2 −1=0 (s^2 )^3 +2(s^2 )^2 +2(s^2 )=0 s^2 =u−(2/3) u^3 +(2/3)u−((47)/(27))=0 Cardano′s solution u=((((47)/(54))+((√(249))/(18))))^(1/3) −((−((47)/(54))+((√(249))/(18))))^(1/3) it makes no sense to go on with this u≈1.01987663 ⇒ s^2 =.353209964 ⇒ sin x ≈±.594314701 testing leads to sin x ≈.594314701 ⇒ x≈2nπ+2.50517939∨x≈2nπ+.636413265](Q155253.png)
$$\mathrm{sin}^{\mathrm{3}} \:{x}\:+\mathrm{sin}\:{x}\:=\mathrm{cos}\:{x} \\ $$$$\mathrm{sin}^{\mathrm{3}} \:{x}\:+\mathrm{sin}\:{x}\:=\pm\sqrt{\mathrm{1}−\mathrm{sin}^{\mathrm{2}} \:{x}} \\ $$$$\mathrm{sin}\:{x}\:={s} \\ $$$${s}^{\mathrm{3}} +{s}=\pm\sqrt{\mathrm{1}+{s}^{\mathrm{2}} } \\ $$$$\mathrm{squaring}\:\left[\mathrm{might}\:\mathrm{introduce}\:\mathrm{false}\:\mathrm{solutions}\right] \\ $$$$\mathrm{and}\:\mathrm{transforming} \\ $$$${s}^{\mathrm{6}} +\mathrm{2}{s}^{\mathrm{4}} +\mathrm{2}{s}^{\mathrm{2}} −\mathrm{1}=\mathrm{0} \\ $$$$\left({s}^{\mathrm{2}} \right)^{\mathrm{3}} +\mathrm{2}\left({s}^{\mathrm{2}} \right)^{\mathrm{2}} +\mathrm{2}\left({s}^{\mathrm{2}} \right)=\mathrm{0} \\ $$$${s}^{\mathrm{2}} ={u}−\frac{\mathrm{2}}{\mathrm{3}} \\ $$$${u}^{\mathrm{3}} +\frac{\mathrm{2}}{\mathrm{3}}{u}−\frac{\mathrm{47}}{\mathrm{27}}=\mathrm{0} \\ $$$$\mathrm{Cardano}'\mathrm{s}\:\mathrm{solution} \\ $$$${u}=\sqrt[{\mathrm{3}}]{\frac{\mathrm{47}}{\mathrm{54}}+\frac{\sqrt{\mathrm{249}}}{\mathrm{18}}}−\sqrt[{\mathrm{3}}]{−\frac{\mathrm{47}}{\mathrm{54}}+\frac{\sqrt{\mathrm{249}}}{\mathrm{18}}} \\ $$$$\mathrm{it}\:\mathrm{makes}\:\mathrm{no}\:\mathrm{sense}\:\mathrm{to}\:\mathrm{go}\:\mathrm{on}\:\mathrm{with}\:\mathrm{this} \\ $$$${u}\approx\mathrm{1}.\mathrm{01987663} \\ $$$$\Rightarrow \\ $$$${s}^{\mathrm{2}} =.\mathrm{353209964} \\ $$$$\Rightarrow \\ $$$$\mathrm{sin}\:{x}\:\approx\pm.\mathrm{594314701} \\ $$$$\mathrm{testing}\:\mathrm{leads}\:\mathrm{to} \\ $$$$\mathrm{sin}\:{x}\:\approx.\mathrm{594314701} \\ $$$$\Rightarrow \\ $$$${x}\approx\mathrm{2}{n}\pi+\mathrm{2}.\mathrm{50517939}\vee{x}\approx\mathrm{2}{n}\pi+.\mathrm{636413265} \\ $$
Commented by mathdanisur last updated on 27/Sep/21
$$\mathrm{Very}\:\mathrm{nice}\:\boldsymbol{\mathrm{S}}\mathrm{er},\:\mathrm{thank}\:\mathrm{you} \\ $$
