Question and Answers Forum

All Questions      Topic List

Algebra Questions

Previous in All Question      Next in All Question      

Previous in Algebra      Next in Algebra      

Question Number 155345 by mathdanisur last updated on 29/Sep/21

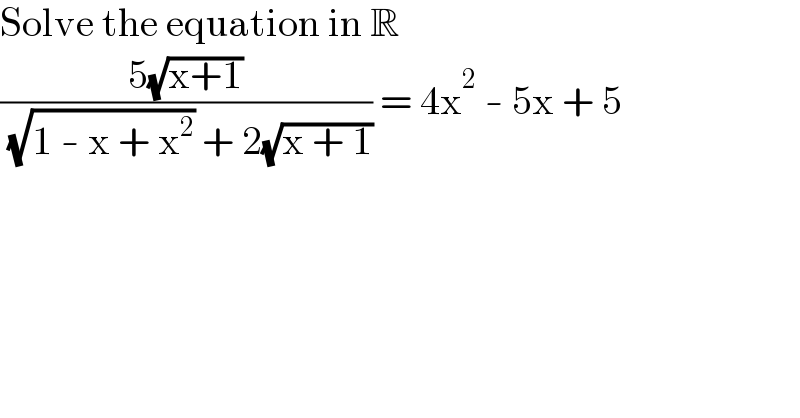
Solve the equation in R ((5(√(x+1)))/( (√(1 - x + x^2 )) + 2(√(x + 1)))) = 4x^2 - 5x + 5

$$\mathrm{Solve}\:\mathrm{the}\:\mathrm{equation}\:\mathrm{in}\:\mathbb{R} \\ $$$$\frac{\mathrm{5}\sqrt{\mathrm{x}+\mathrm{1}}}{\:\sqrt{\mathrm{1}\:-\:\mathrm{x}\:+\:\mathrm{x}^{\mathrm{2}} }\:+\:\mathrm{2}\sqrt{\mathrm{x}\:+\:\mathrm{1}}}\:=\:\mathrm{4x}^{\mathrm{2}} \:-\:\mathrm{5x}\:+\:\mathrm{5} \\ $$

Commented by MJS_new last updated on 29/Sep/21

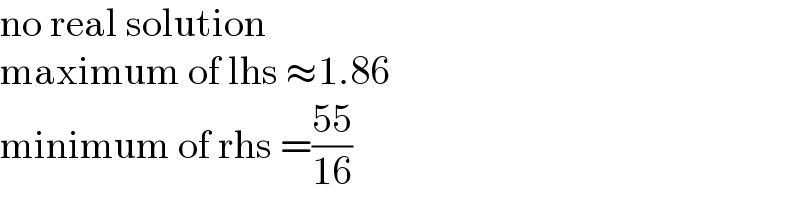
no real solution maximum of lhs ≈1.86 minimum of rhs =((55)/(16))

$$\mathrm{no}\:\mathrm{real}\:\mathrm{solution} \\ $$$$\mathrm{maximum}\:\mathrm{of}\:\mathrm{lhs}\:\approx\mathrm{1}.\mathrm{86} \\ $$$$\mathrm{minimum}\:\mathrm{of}\:\mathrm{rhs}\:=\frac{\mathrm{55}}{\mathrm{16}} \\ $$

Answered by ArielVyny last updated on 29/Sep/21

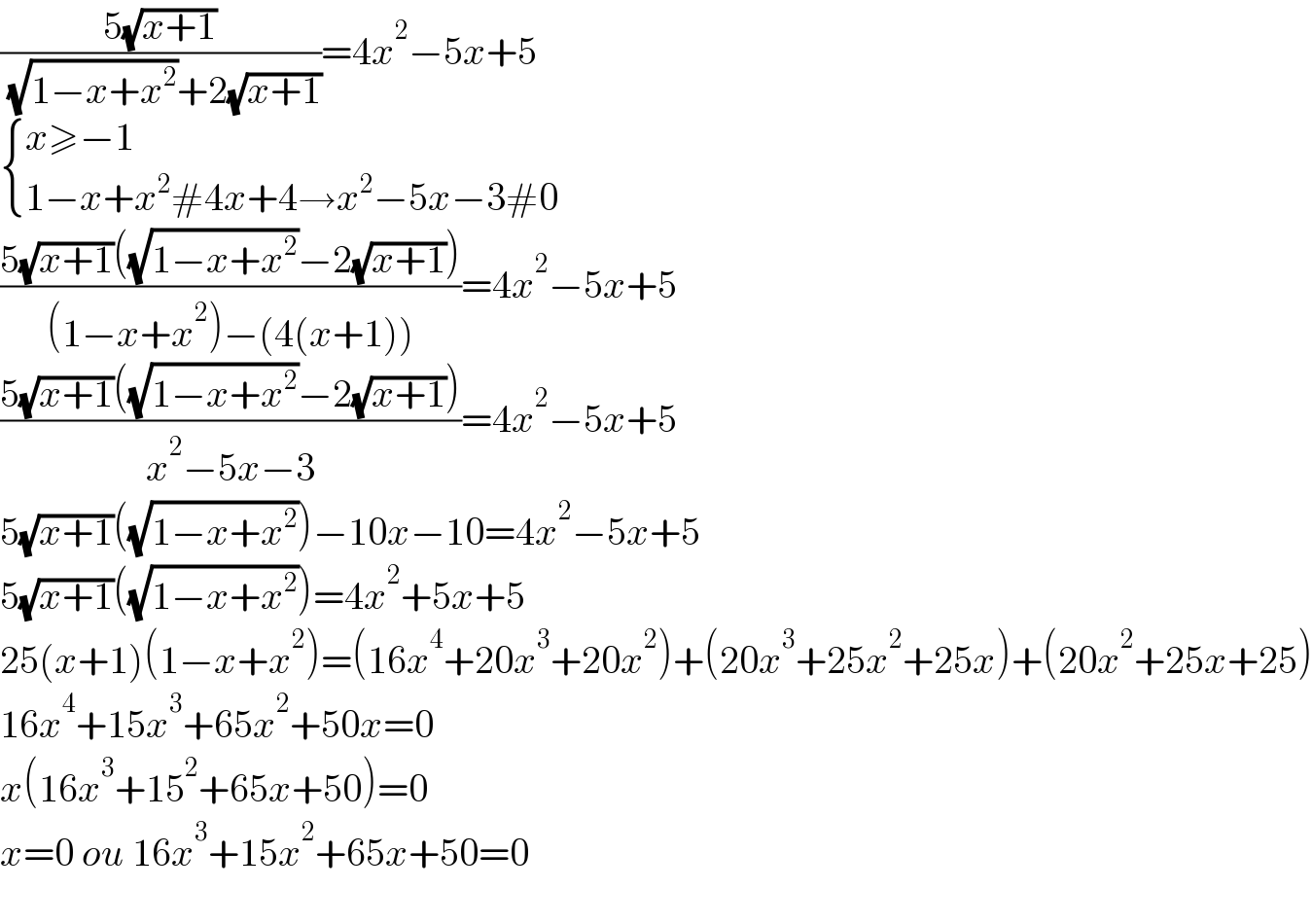
((5(√(x+1)))/( (√(1−x+x^2 ))+2(√(x+1))))=4x^2 −5x+5 { ((x≥−1)),((1−x+x^2 #4x+4→x^2 −5x−3#0)) :} ((5(√(x+1))((√(1−x+x^2 ))−2(√(x+1))))/((1−x+x^2 )−(4(x+1))))=4x^2 −5x+5 ((5(√(x+1))((√(1−x+x^2 ))−2(√(x+1))))/(x^2 −5x−3))=4x^2 −5x+5 5(√(x+1))((√(1−x+x^2 )))−10x−10=4x^2 −5x+5 5(√(x+1))((√(1−x+x^2 )))=4x^2 +5x+5 25(x+1)(1−x+x^2 )=(16x^4 +20x^3 +20x^2 )+(20x^3 +25x^2 +25x)+(20x^2 +25x+25) 16x^4 +15x^3 +65x^2 +50x=0 x(16x^3 +15^2 +65x+50)=0 x=0 ou 16x^3 +15x^2 +65x+50=0

$$\frac{\mathrm{5}\sqrt{{x}+\mathrm{1}}}{\:\sqrt{\mathrm{1}−{x}+{x}^{\mathrm{2}} }+\mathrm{2}\sqrt{{x}+\mathrm{1}}}=\mathrm{4}{x}^{\mathrm{2}} −\mathrm{5}{x}+\mathrm{5} \\ $$$$\begin{cases}{{x}\geqslant−\mathrm{1}}\\{\mathrm{1}−{x}+{x}^{\mathrm{2}} #\mathrm{4}{x}+\mathrm{4}\rightarrow{x}^{\mathrm{2}} −\mathrm{5}{x}−\mathrm{3}#\mathrm{0}}\end{cases} \\ $$$$\frac{\mathrm{5}\sqrt{{x}+\mathrm{1}}\left(\sqrt{\mathrm{1}−{x}+{x}^{\mathrm{2}} }−\mathrm{2}\sqrt{{x}+\mathrm{1}}\right)}{\left(\mathrm{1}−{x}+{x}^{\mathrm{2}} \right)−\left(\mathrm{4}\left({x}+\mathrm{1}\right)\right)}=\mathrm{4}{x}^{\mathrm{2}} −\mathrm{5}{x}+\mathrm{5} \\ $$$$\frac{\mathrm{5}\sqrt{{x}+\mathrm{1}}\left(\sqrt{\mathrm{1}−{x}+{x}^{\mathrm{2}} }−\mathrm{2}\sqrt{{x}+\mathrm{1}}\right)}{{x}^{\mathrm{2}} −\mathrm{5}{x}−\mathrm{3}}=\mathrm{4}{x}^{\mathrm{2}} −\mathrm{5}{x}+\mathrm{5} \\ $$$$\mathrm{5}\sqrt{{x}+\mathrm{1}}\left(\sqrt{\mathrm{1}−{x}+{x}^{\mathrm{2}} }\right)−\mathrm{10}{x}−\mathrm{10}=\mathrm{4}{x}^{\mathrm{2}} −\mathrm{5}{x}+\mathrm{5} \\ $$$$\mathrm{5}\sqrt{{x}+\mathrm{1}}\left(\sqrt{\mathrm{1}−{x}+{x}^{\mathrm{2}} }\right)=\mathrm{4}{x}^{\mathrm{2}} +\mathrm{5}{x}+\mathrm{5} \\ $$$$\mathrm{25}\left({x}+\mathrm{1}\right)\left(\mathrm{1}−{x}+{x}^{\mathrm{2}} \right)=\left(\mathrm{16}{x}^{\mathrm{4}} +\mathrm{20}{x}^{\mathrm{3}} +\mathrm{20}{x}^{\mathrm{2}} \right)+\left(\mathrm{20}{x}^{\mathrm{3}} +\mathrm{25}{x}^{\mathrm{2}} +\mathrm{25}{x}\right)+\left(\mathrm{20}{x}^{\mathrm{2}} +\mathrm{25}{x}+\mathrm{25}\right) \\ $$$$\mathrm{16}{x}^{\mathrm{4}} +\mathrm{15}{x}^{\mathrm{3}} +\mathrm{65}{x}^{\mathrm{2}} +\mathrm{50}{x}=\mathrm{0} \\ $$$${x}\left(\mathrm{16}{x}^{\mathrm{3}} +\mathrm{15}^{\mathrm{2}} +\mathrm{65}{x}+\mathrm{50}\right)=\mathrm{0} \\ $$$${x}=\mathrm{0}\:{ou}\:\mathrm{16}{x}^{\mathrm{3}} +\mathrm{15}{x}^{\mathrm{2}} +\mathrm{65}{x}+\mathrm{50}=\mathrm{0} \\ $$$$ \\ $$

Commented by MJS_new last updated on 29/Sep/21

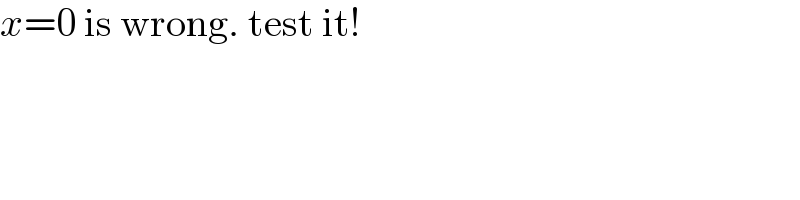
x=0 is wrong. test it!

$${x}=\mathrm{0}\:\mathrm{is}\:\mathrm{wrong}.\:\mathrm{test}\:\mathrm{it}! \\ $$

Commented by ArielVyny last updated on 29/Sep/21

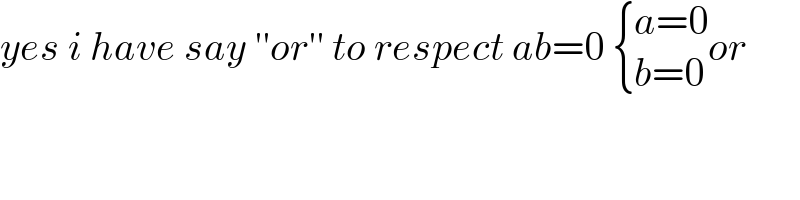
yes i have say ′′or′′ to respect ab=0 { ((a=0)),((b=0)) :}or

$${yes}\:{i}\:{have}\:{say}\:''{or}''\:{to}\:{respect}\:{ab}=\mathrm{0}\:\begin{cases}{{a}=\mathrm{0}}\\{{b}=\mathrm{0}}\end{cases}{or} \\ $$

Answered by MJS_new last updated on 29/Sep/21

((5(√(x+1)))/( (√(x^2 −x+1))+2(√(x+1))))=4x^2 −5x+5 −(8x^2 −10x+5)(√(x+1))=(4x^2 −5x+5)(√(x^2 −x+1)) squaring (might introduce false solutions) and teansforming x^2 (x^4 −((15)/2)x^3 +((217)/(16))x^2 −((175)/(16))x+((15)/4))=0 obviously x=0 is false x^4 −((15)/2)x^3 +((217)/(16))x^2 −((175)/(16))x+((15)/4)=0 (x^2 −((25)/4)x+5)(x^2 −(5/4)x+(3/4))=0 x=((25)/8)±((√(305))/8) [both false] x=(5/8)±((√(23))/8)i [both true]

$$\frac{\mathrm{5}\sqrt{{x}+\mathrm{1}}}{\:\sqrt{{x}^{\mathrm{2}} −{x}+\mathrm{1}}+\mathrm{2}\sqrt{{x}+\mathrm{1}}}=\mathrm{4}{x}^{\mathrm{2}} −\mathrm{5}{x}+\mathrm{5} \\ $$$$−\left(\mathrm{8}{x}^{\mathrm{2}} −\mathrm{10}{x}+\mathrm{5}\right)\sqrt{{x}+\mathrm{1}}=\left(\mathrm{4}{x}^{\mathrm{2}} −\mathrm{5}{x}+\mathrm{5}\right)\sqrt{{x}^{\mathrm{2}} −{x}+\mathrm{1}} \\ $$$$\mathrm{squaring}\:\left(\mathrm{might}\:\mathrm{introduce}\:\mathrm{false}\:\mathrm{solutions}\right) \\ $$$$\mathrm{and}\:\mathrm{teansforming} \\ $$$${x}^{\mathrm{2}} \left({x}^{\mathrm{4}} −\frac{\mathrm{15}}{\mathrm{2}}{x}^{\mathrm{3}} +\frac{\mathrm{217}}{\mathrm{16}}{x}^{\mathrm{2}} −\frac{\mathrm{175}}{\mathrm{16}}{x}+\frac{\mathrm{15}}{\mathrm{4}}\right)=\mathrm{0} \\ $$$$\mathrm{obviously}\:{x}=\mathrm{0}\:\mathrm{is}\:\mathrm{false} \\ $$$${x}^{\mathrm{4}} −\frac{\mathrm{15}}{\mathrm{2}}{x}^{\mathrm{3}} +\frac{\mathrm{217}}{\mathrm{16}}{x}^{\mathrm{2}} −\frac{\mathrm{175}}{\mathrm{16}}{x}+\frac{\mathrm{15}}{\mathrm{4}}=\mathrm{0} \\ $$$$\left({x}^{\mathrm{2}} −\frac{\mathrm{25}}{\mathrm{4}}{x}+\mathrm{5}\right)\left({x}^{\mathrm{2}} −\frac{\mathrm{5}}{\mathrm{4}}{x}+\frac{\mathrm{3}}{\mathrm{4}}\right)=\mathrm{0} \\ $$$${x}=\frac{\mathrm{25}}{\mathrm{8}}\pm\frac{\sqrt{\mathrm{305}}}{\mathrm{8}}\:\left[\mathrm{both}\:\mathrm{false}\right] \\ $$$${x}=\frac{\mathrm{5}}{\mathrm{8}}\pm\frac{\sqrt{\mathrm{23}}}{\mathrm{8}}\mathrm{i}\:\left[\mathrm{both}\:\mathrm{true}\right] \\ $$

Commented by mathdanisur last updated on 29/Sep/21

Very nice solution Ser thank you

$$\mathrm{Very}\:\mathrm{nice}\:\mathrm{solution}\:\boldsymbol{\mathrm{S}}\mathrm{er}\:\mathrm{thank}\:\mathrm{you} \\ $$

Commented by mathdanisur last updated on 30/Sep/21

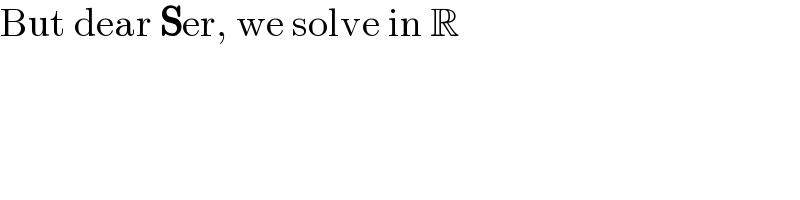
But dear Ser, we solve in R

$$\mathrm{But}\:\mathrm{dear}\:\boldsymbol{\mathrm{S}}\mathrm{er},\:\mathrm{we}\:\mathrm{solve}\:\mathrm{in}\:\mathbb{R} \\ $$

Commented by MJS_new last updated on 30/Sep/21

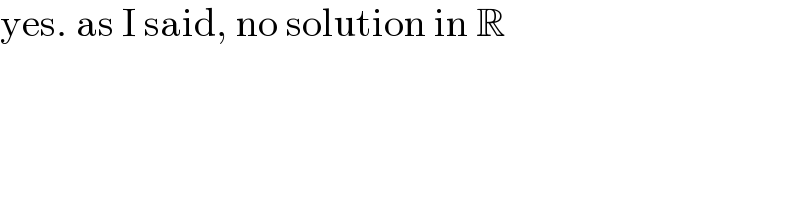
yes. as I said, no solution in R

$$\mathrm{yes}.\:\mathrm{as}\:\mathrm{I}\:\mathrm{said},\:\mathrm{no}\:\mathrm{solution}\:\mathrm{in}\:\mathbb{R} \\ $$

Commented by mathdanisur last updated on 30/Sep/21

THANKYOU DEAR SER

$$\mathrm{THANKYOU}\:\mathrm{DEAR}\:\mathrm{SER} \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com