
Question Number 145109 by mathdanisur last updated on 02/Jul/21
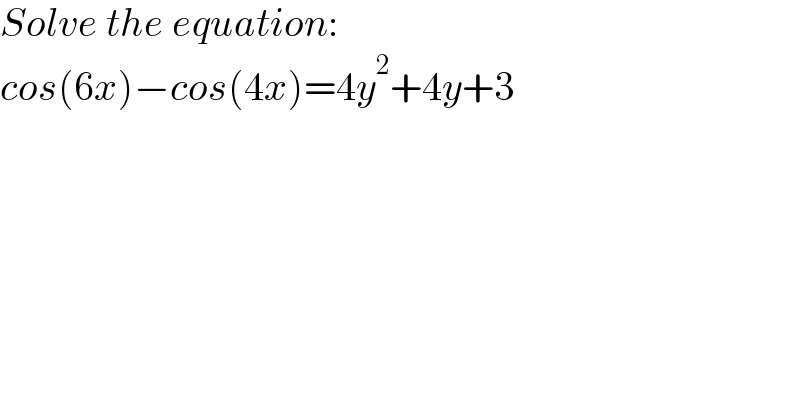
$${Solve}\:{the}\:{equation}: \\ $$$${cos}\left(\mathrm{6}{x}\right)−{cos}\left(\mathrm{4}{x}\right)=\mathrm{4}{y}^{\mathrm{2}} +\mathrm{4}{y}+\mathrm{3} \\ $$
Answered by mitica last updated on 02/Jul/21
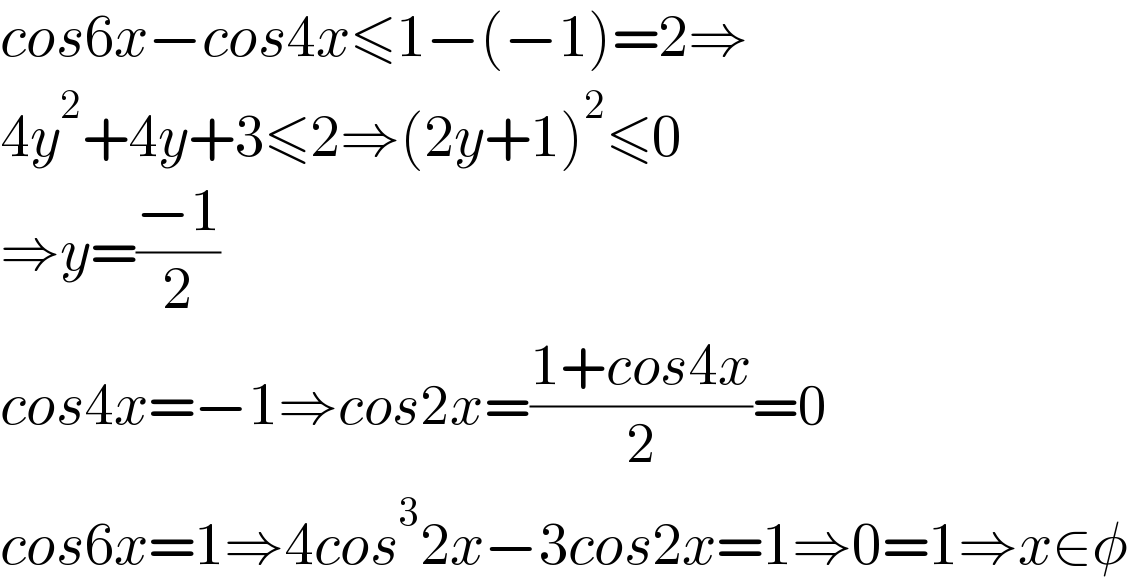
$${cos}\mathrm{6}{x}−{cos}\mathrm{4}{x}\leqslant\mathrm{1}−\left(−\mathrm{1}\right)=\mathrm{2}\Rightarrow \\ $$$$\mathrm{4}{y}^{\mathrm{2}} +\mathrm{4}{y}+\mathrm{3}\leqslant\mathrm{2}\Rightarrow\left(\mathrm{2}{y}+\mathrm{1}\right)^{\mathrm{2}} \leqslant\mathrm{0} \\ $$$$\Rightarrow{y}=\frac{−\mathrm{1}}{\mathrm{2}} \\ $$$${cos}\mathrm{4}{x}=−\mathrm{1}\Rightarrow{cos}\mathrm{2}{x}=\frac{\mathrm{1}+{cos}\mathrm{4}{x}}{\mathrm{2}}=\mathrm{0} \\ $$$${cos}\mathrm{6}{x}=\mathrm{1}\Rightarrow\mathrm{4}{cos}^{\mathrm{3}} \mathrm{2}{x}−\mathrm{3}{cos}\mathrm{2}{x}=\mathrm{1}\Rightarrow\mathrm{0}=\mathrm{1}\Rightarrow{x}\in\phi \\ $$
Commented by mathdanisur last updated on 02/Jul/21
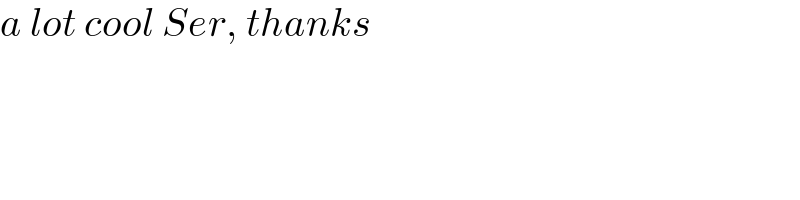
$${a}\:{lot}\:{cool}\:{Ser},\:{thanks} \\ $$
