
Question Number 48361 by peter frank last updated on 22/Nov/18
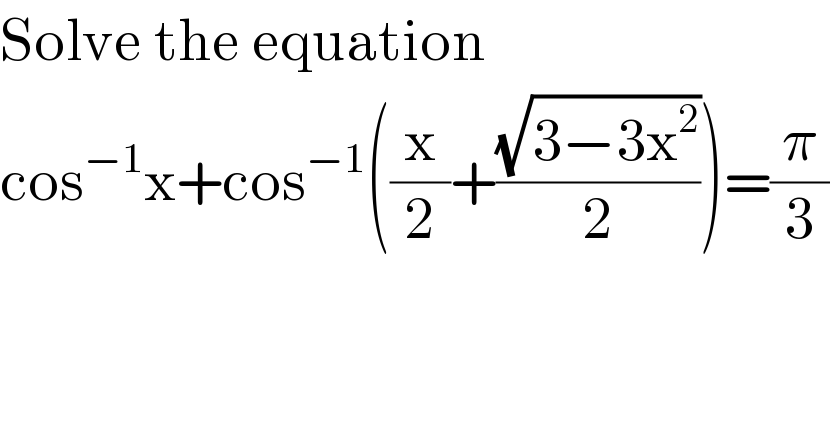
$$\mathrm{Solve}\:\mathrm{the}\:\mathrm{equation} \\ $$$$\mathrm{cos}^{−\mathrm{1}} \mathrm{x}+\mathrm{cos}^{−\mathrm{1}} \left(\frac{\mathrm{x}}{\mathrm{2}}+\frac{\sqrt{\mathrm{3}−\mathrm{3x}^{\mathrm{2}} }}{\mathrm{2}}\right)=\frac{\pi}{\mathrm{3}} \\ $$
Commented by MJS last updated on 22/Nov/18

$$\mathrm{it}'\mathrm{s}\:\mathrm{true}\:\mathrm{for}\:{x}\geqslant\frac{\mathrm{1}}{\mathrm{2}} \\ $$
Answered by behi83417@gmail.com last updated on 22/Nov/18
![this is not an equation. let:a=cos^(−1) x,b=cos^(−1) ((x/2)+((√(3−3x^2 ))/2)) cosb=(x/2)+((√(3−3x^2 ))/2)=(1/2).x+((√3)/2).(√(1−x^2 ))= =cos(π/3)cosa+sin(π/3).sina=cos((π/3)−a) ⇒b=(π/3)−a⇒a+b=(π/3),for:x∈[−1,1].](Q48370.png)
$${this}\:{is}\:{not}\:{an}\:{equation}. \\ $$$${let}:{a}={cos}^{−\mathrm{1}} {x},{b}={cos}^{−\mathrm{1}} \left(\frac{{x}}{\mathrm{2}}+\frac{\sqrt{\mathrm{3}−\mathrm{3}{x}^{\mathrm{2}} }}{\mathrm{2}}\right) \\ $$$${cosb}=\frac{{x}}{\mathrm{2}}+\frac{\sqrt{\mathrm{3}−\mathrm{3}{x}^{\mathrm{2}} }}{\mathrm{2}}=\frac{\mathrm{1}}{\mathrm{2}}.{x}+\frac{\sqrt{\mathrm{3}}}{\mathrm{2}}.\sqrt{\mathrm{1}−{x}^{\mathrm{2}} }= \\ $$$$={cos}\frac{\pi}{\mathrm{3}}{cosa}+{sin}\frac{\pi}{\mathrm{3}}.{sina}={cos}\left(\frac{\pi}{\mathrm{3}}−{a}\right) \\ $$$$\Rightarrow{b}=\frac{\pi}{\mathrm{3}}−{a}\Rightarrow{a}+{b}=\frac{\pi}{\mathrm{3}},{for}:{x}\in\left[−\mathrm{1},\mathrm{1}\right]. \\ $$
