Question and Answers Forum

All Questions      Topic List

None Questions

Previous in All Question      Next in All Question      

Previous in None      Next in None      

Question Number 197753 by tri26112004 last updated on 27/Sep/23

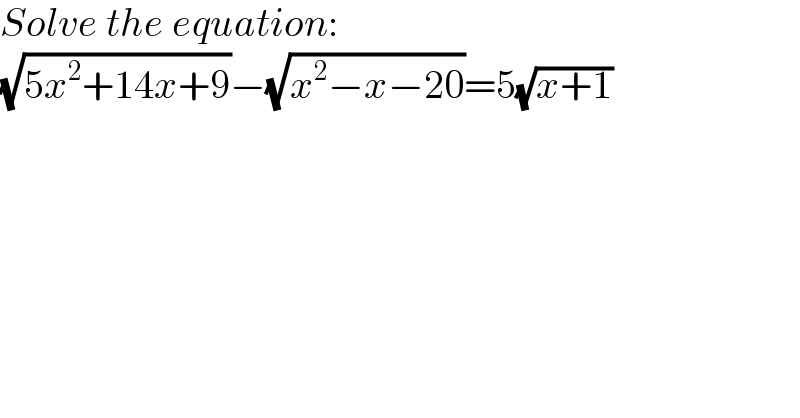
Solve the equation: (√(5x^2 +14x+9))−(√(x^2 −x−20))=5(√(x+1))

$${Solve}\:{the}\:{equation}: \\ $$$$\sqrt{\mathrm{5}{x}^{\mathrm{2}} +\mathrm{14}{x}+\mathrm{9}}−\sqrt{{x}^{\mathrm{2}} −{x}−\mathrm{20}}=\mathrm{5}\sqrt{{x}+\mathrm{1}} \\ $$

Answered by Frix last updated on 27/Sep/23

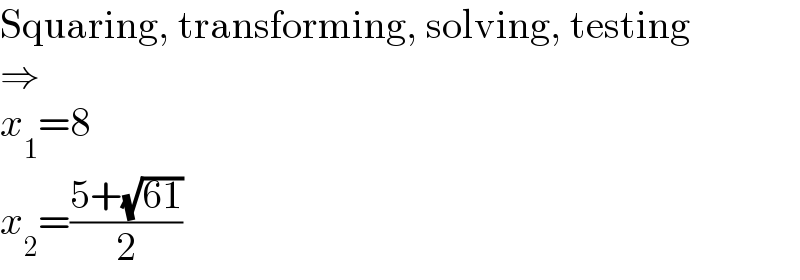
Squaring, transforming, solving, testing ⇒ x_1 =8 x_2 =((5+(√(61)))/2)

$$\mathrm{Squaring},\:\mathrm{transforming},\:\mathrm{solving},\:\mathrm{testing} \\ $$$$\Rightarrow \\ $$$${x}_{\mathrm{1}} =\mathrm{8} \\ $$$${x}_{\mathrm{2}} =\frac{\mathrm{5}+\sqrt{\mathrm{61}}}{\mathrm{2}} \\ $$

Commented by tri26112004 last updated on 27/Sep/23

can you show your solution

$${can}\:{you}\:{show}\:{your}\:{solution} \\ $$

Commented by Frix last updated on 27/Sep/23

(√a)−(√b)=(√c) (√a)=(√b)+(√c) a=b+2(√(bc))+c a−(b+c)=2(√(bc)) (a−(b+c))^2 =4bc a^2 +b^2 +c^2 −2(ab+ac+bc)=0 Now insert a=5x^2 +14x+9 b=x^2 −x−20 c=25(x+1) x^4 −((45x^3 )/4)+((33x^2 )/4)+((505x)/4)+126=0 (x−8)(x+(7/4))(x^2 −5x−9)=0 Test the solutions, some might be false due to squaring

$$\sqrt{{a}}−\sqrt{{b}}=\sqrt{{c}} \\ $$$$\sqrt{{a}}=\sqrt{{b}}+\sqrt{{c}} \\ $$$${a}={b}+\mathrm{2}\sqrt{{bc}}+{c} \\ $$$${a}−\left({b}+{c}\right)=\mathrm{2}\sqrt{{bc}} \\ $$$$\left({a}−\left({b}+{c}\right)\right)^{\mathrm{2}} =\mathrm{4}{bc} \\ $$$${a}^{\mathrm{2}} +{b}^{\mathrm{2}} +{c}^{\mathrm{2}} −\mathrm{2}\left({ab}+{ac}+{bc}\right)=\mathrm{0} \\ $$$$\mathrm{Now}\:\mathrm{insert} \\ $$$${a}=\mathrm{5}{x}^{\mathrm{2}} +\mathrm{14}{x}+\mathrm{9} \\ $$$${b}={x}^{\mathrm{2}} −{x}−\mathrm{20} \\ $$$${c}=\mathrm{25}\left({x}+\mathrm{1}\right) \\ $$$${x}^{\mathrm{4}} −\frac{\mathrm{45}{x}^{\mathrm{3}} }{\mathrm{4}}+\frac{\mathrm{33}{x}^{\mathrm{2}} }{\mathrm{4}}+\frac{\mathrm{505}{x}}{\mathrm{4}}+\mathrm{126}=\mathrm{0} \\ $$$$\left({x}−\mathrm{8}\right)\left({x}+\frac{\mathrm{7}}{\mathrm{4}}\right)\left({x}^{\mathrm{2}} −\mathrm{5}{x}−\mathrm{9}\right)=\mathrm{0} \\ $$$$\mathrm{Test}\:\mathrm{the}\:\mathrm{solutions},\:\mathrm{some}\:\mathrm{might}\:\mathrm{be}\:\mathrm{false}\:\mathrm{due} \\ $$$$\mathrm{to}\:\mathrm{squaring} \\ $$

Commented by tri26112004 last updated on 28/Sep/23

Do you have another solution¿

$${Do}\:{you}\:{have}\:{another}\:{solution}¿ \\ $$

Commented by tri26112004 last updated on 28/Sep/23

Such as Using Inequality

$${Such}\:{as}\:{Using}\:{Inequality} \\ $$

Answered by Rasheed.Sindhi last updated on 28/Sep/23

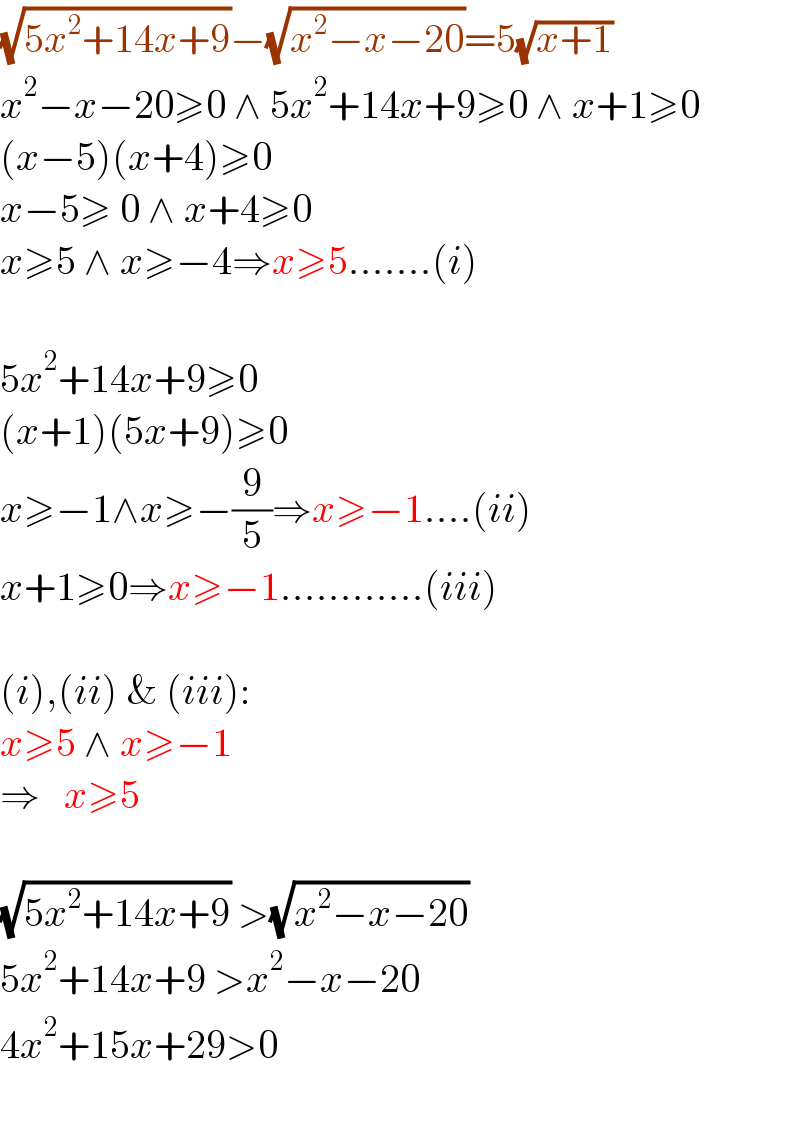
(√(5x^2 +14x+9))−(√(x^2 −x−20))=5(√(x+1)) x^2 −x−20≥0 ∧ 5x^2 +14x+9≥0 ∧ x+1≥0 (x−5)(x+4)≥0 x−5≥ 0 ∧ x+4≥0 x≥5 ∧ x≥−4⇒x≥5.......(i) 5x^2 +14x+9≥0 (x+1)(5x+9)≥0 x≥−1∧x≥−(9/5)⇒x≥−1....(ii) x+1≥0⇒x≥−1............(iii) (i),(ii) & (iii): x≥5 ∧ x≥−1 ⇒ x≥5 (√(5x^2 +14x+9)) >(√(x^2 −x−20)) 5x^2 +14x+9 >x^2 −x−20 4x^2 +15x+29>0

$$\sqrt{\mathrm{5}{x}^{\mathrm{2}} +\mathrm{14}{x}+\mathrm{9}}−\sqrt{{x}^{\mathrm{2}} −{x}−\mathrm{20}}=\mathrm{5}\sqrt{{x}+\mathrm{1}} \\ $$$${x}^{\mathrm{2}} −{x}−\mathrm{20}\geqslant\mathrm{0}\:\wedge\:\mathrm{5}{x}^{\mathrm{2}} +\mathrm{14}{x}+\mathrm{9}\geqslant\mathrm{0}\:\wedge\:{x}+\mathrm{1}\geqslant\mathrm{0} \\ $$$$\left({x}−\mathrm{5}\right)\left({x}+\mathrm{4}\right)\geqslant\mathrm{0} \\ $$$${x}−\mathrm{5}\geqslant\:\mathrm{0}\:\wedge\:{x}+\mathrm{4}\geqslant\mathrm{0} \\ $$$${x}\geqslant\mathrm{5}\:\wedge\:{x}\geqslant−\mathrm{4}\Rightarrow{x}\geqslant\mathrm{5}.......\left({i}\right) \\ $$$$ \\ $$$$\mathrm{5}{x}^{\mathrm{2}} +\mathrm{14}{x}+\mathrm{9}\geqslant\mathrm{0} \\ $$$$\left({x}+\mathrm{1}\right)\left(\mathrm{5}{x}+\mathrm{9}\right)\geqslant\mathrm{0} \\ $$$${x}\geqslant−\mathrm{1}\wedge{x}\geqslant−\frac{\mathrm{9}}{\mathrm{5}}\Rightarrow{x}\geqslant−\mathrm{1}....\left({ii}\right) \\ $$$${x}+\mathrm{1}\geqslant\mathrm{0}\Rightarrow{x}\geqslant−\mathrm{1}............\left({iii}\right) \\ $$$$ \\ $$$$\left({i}\right),\left({ii}\right)\:\&\:\left({iii}\right): \\ $$$${x}\geqslant\mathrm{5}\:\wedge\:{x}\geqslant−\mathrm{1} \\ $$$$\Rightarrow\:\:\:{x}\geqslant\mathrm{5} \\ $$$$ \\ $$$$\sqrt{\mathrm{5}{x}^{\mathrm{2}} +\mathrm{14}{x}+\mathrm{9}}\:>\sqrt{{x}^{\mathrm{2}} −{x}−\mathrm{20}} \\ $$$$\mathrm{5}{x}^{\mathrm{2}} +\mathrm{14}{x}+\mathrm{9}\:>{x}^{\mathrm{2}} −{x}−\mathrm{20} \\ $$$$\mathrm{4}{x}^{\mathrm{2}} +\mathrm{15}{x}+\mathrm{29}>\mathrm{0} \\ $$$$ \\ $$

Commented by tri26112004 last updated on 28/Sep/23

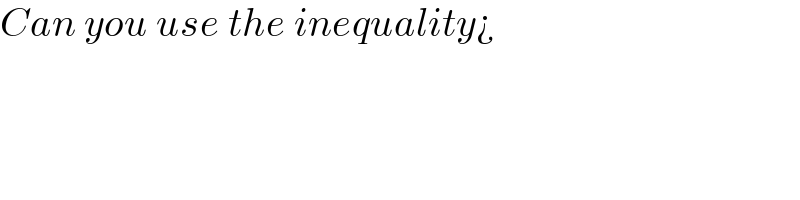
Can you use the inequality¿

$${Can}\:{you}\:{use}\:{the}\:{inequality}¿ \\ $$

Commented by Rasheed.Sindhi last updated on 28/Sep/23

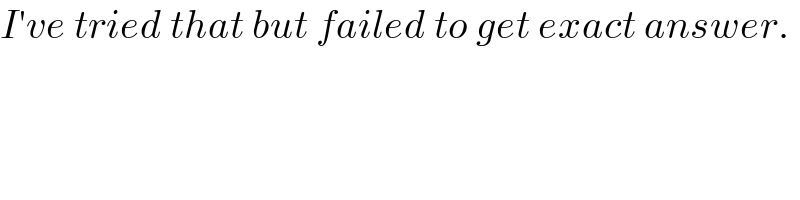
I′ve tried that but failed to get exact answer.

$${I}'{ve}\:{tried}\:{that}\:{but}\:{failed}\:{to}\:{get}\:{exact}\:{answer}. \\ $$

Commented by tri26112004 last updated on 28/Sep/23

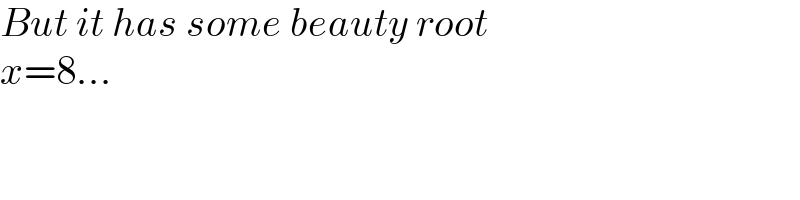
But it has some beauty root x=8...

$${But}\:{it}\:{has}\:{some}\:{beauty}\:{root} \\ $$$${x}=\mathrm{8}... \\ $$

Commented by Frix last updated on 28/Sep/23

The solution method doesn′t care whether you like the solution or not.

$$\mathrm{The}\:\mathrm{solution}\:\mathrm{method}\:\mathrm{doesn}'\mathrm{t}\:\mathrm{care}\:\mathrm{whether} \\ $$$$\mathrm{you}\:\mathrm{like}\:\mathrm{the}\:\mathrm{solution}\:\mathrm{or}\:\mathrm{not}. \\ $$

Commented by tri26112004 last updated on 28/Sep/23

okay

$${okay} \\ $$

Answered by ajfour last updated on 28/Sep/23

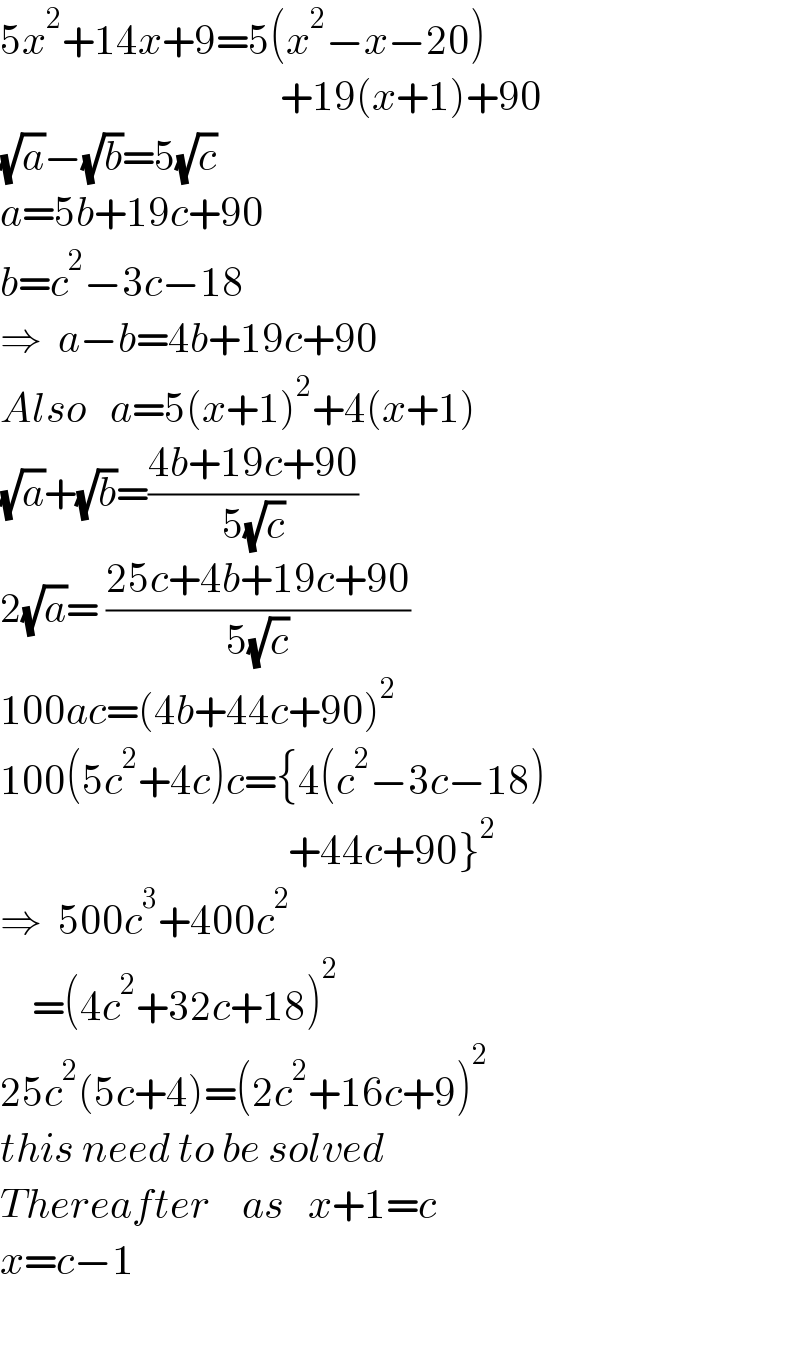
5x^2 +14x+9=5(x^2 −x−20) +19(x+1)+90 (√a)−(√b)=5(√c) a=5b+19c+90 b=c^2 −3c−18 ⇒ a−b=4b+19c+90 Also a=5(x+1)^2 +4(x+1) (√a)+(√b)=((4b+19c+90)/(5(√c))) 2(√a)= ((25c+4b+19c+90)/(5(√c))) 100ac=(4b+44c+90)^2 100(5c^2 +4c)c={4(c^2 −3c−18) +44c+90}^2 ⇒ 500c^3 +400c^2 =(4c^2 +32c+18)^2 25c^2 (5c+4)=(2c^2 +16c+9)^2 this need to be solved Thereafter as x+1=c x=c−1

$$\mathrm{5}{x}^{\mathrm{2}} +\mathrm{14}{x}+\mathrm{9}=\mathrm{5}\left({x}^{\mathrm{2}} −{x}−\mathrm{20}\right) \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:+\mathrm{19}\left({x}+\mathrm{1}\right)+\mathrm{90} \\ $$$$\sqrt{{a}}−\sqrt{{b}}=\mathrm{5}\sqrt{{c}} \\ $$$${a}=\mathrm{5}{b}+\mathrm{19}{c}+\mathrm{90} \\ $$$${b}={c}^{\mathrm{2}} −\mathrm{3}{c}−\mathrm{18} \\ $$$$\Rightarrow\:\:{a}−{b}=\mathrm{4}{b}+\mathrm{19}{c}+\mathrm{90} \\ $$$${Also}\:\:\:{a}=\mathrm{5}\left({x}+\mathrm{1}\right)^{\mathrm{2}} +\mathrm{4}\left({x}+\mathrm{1}\right) \\ $$$$\sqrt{{a}}+\sqrt{{b}}=\frac{\mathrm{4}{b}+\mathrm{19}{c}+\mathrm{90}}{\mathrm{5}\sqrt{{c}}} \\ $$$$\mathrm{2}\sqrt{{a}}=\:\frac{\mathrm{25}{c}+\mathrm{4}{b}+\mathrm{19}{c}+\mathrm{90}}{\mathrm{5}\sqrt{{c}}} \\ $$$$\mathrm{100}{ac}=\left(\mathrm{4}{b}+\mathrm{44}{c}+\mathrm{90}\right)^{\mathrm{2}} \\ $$$$\mathrm{100}\left(\mathrm{5}{c}^{\mathrm{2}} +\mathrm{4}{c}\right){c}=\left\{\mathrm{4}\left({c}^{\mathrm{2}} −\mathrm{3}{c}−\mathrm{18}\right)\right. \\ $$$$\left.\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:+\mathrm{44}{c}+\mathrm{90}\right\}^{\mathrm{2}} \\ $$$$\Rightarrow\:\:\mathrm{500}{c}^{\mathrm{3}} +\mathrm{400}{c}^{\mathrm{2}} \\ $$$$\:\:\:\:=\left(\mathrm{4}{c}^{\mathrm{2}} +\mathrm{32}{c}+\mathrm{18}\right)^{\mathrm{2}} \\ $$$$\mathrm{25}{c}^{\mathrm{2}} \left(\mathrm{5}{c}+\mathrm{4}\right)=\left(\mathrm{2}{c}^{\mathrm{2}} +\mathrm{16}{c}+\mathrm{9}\right)^{\mathrm{2}} \\ $$$${this}\:{need}\:{to}\:{be}\:{solved} \\ $$$${Thereafter}\:\:\:\:{as}\:\:\:{x}+\mathrm{1}={c} \\ $$$${x}={c}−\mathrm{1} \\ $$$$ \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com