
Question Number 51680 by Tawa1 last updated on 29/Dec/18
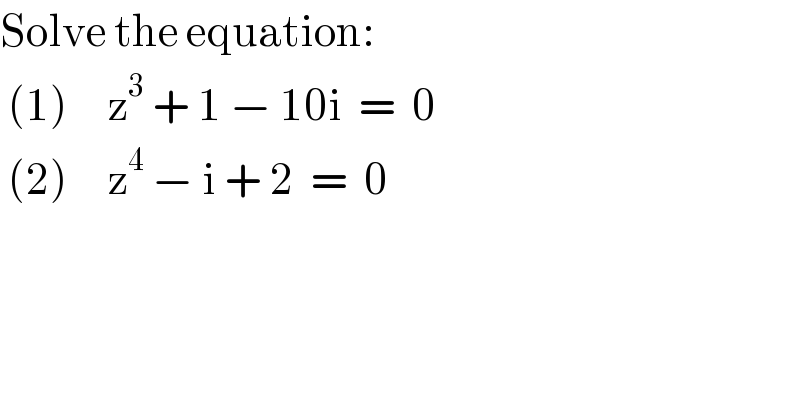
$$\mathrm{Solve}\:\mathrm{the}\:\mathrm{equation}:\:\:\:\:\: \\ $$$$\:\left(\mathrm{1}\right)\:\:\:\:\:\mathrm{z}^{\mathrm{3}} \:+\:\mathrm{1}\:−\:\mathrm{10i}\:\:=\:\:\mathrm{0} \\ $$$$\:\left(\mathrm{2}\right)\:\:\:\:\:\mathrm{z}^{\mathrm{4}} \:−\:\mathrm{i}\:+\:\mathrm{2}\:\:=\:\:\mathrm{0} \\ $$
Commented by maxmathsup by imad last updated on 29/Dec/18
![2) z^4 −i+2=0 ⇔z^4 =−2+i =(√5)(−(2/(√5)) +(i/(√5))) =r(cosθ +i sinθ) ⇒ r=(√5)and cosθ =−(2/(√5)) and sinθ =(1/(√5)) ⇒tanθ =−(1/2) ⇒θ =−arctan((1/2)) ⇒ −2+i =r e^(−i arctan((1/2))) let z =ρ e^(iα) so z^4 =−2+i ⇒ρ^4 =r and 4α=−arctan((1/2))+2kπ ⇒ ρ=^4 (√r) and α_k =−(1/4)arctan((1/2)) +((kπ)/2) with k∈[[0,3]] so the roots of this equation are Z_k =^8 (√5) e^(i(−(1/4)arctan((1/2))+((kπ)/2))) and k∈[[0,3]].](Q51703.png)
$$\left.\mathrm{2}\right)\:\:{z}^{\mathrm{4}} −{i}+\mathrm{2}=\mathrm{0}\:\Leftrightarrow{z}^{\mathrm{4}} =−\mathrm{2}+{i}\:=\sqrt{\mathrm{5}}\left(−\frac{\mathrm{2}}{\sqrt{\mathrm{5}}}\:+\frac{{i}}{\sqrt{\mathrm{5}}}\right)\:={r}\left({cos}\theta\:+{i}\:{sin}\theta\right)\:\Rightarrow \\ $$$${r}=\sqrt{\mathrm{5}}{and}\:{cos}\theta\:=−\frac{\mathrm{2}}{\sqrt{\mathrm{5}}}\:{and}\:{sin}\theta\:=\frac{\mathrm{1}}{\sqrt{\mathrm{5}}}\:\Rightarrow{tan}\theta\:=−\frac{\mathrm{1}}{\mathrm{2}}\:\Rightarrow\theta\:=−{arctan}\left(\frac{\mathrm{1}}{\mathrm{2}}\right)\:\Rightarrow \\ $$$$−\mathrm{2}+{i}\:={r}\:{e}^{−{i}\:{arctan}\left(\frac{\mathrm{1}}{\mathrm{2}}\right)} \:\:\:{let}\:{z}\:=\rho\:{e}^{{i}\alpha} \:\:\:{so}\:{z}^{\mathrm{4}} =−\mathrm{2}+{i}\:\Rightarrow\rho^{\mathrm{4}} ={r}\:\:{and}\:\mathrm{4}\alpha=−{arctan}\left(\frac{\mathrm{1}}{\mathrm{2}}\right)+\mathrm{2}{k}\pi\:\Rightarrow \\ $$$$\rho=^{\mathrm{4}} \sqrt{{r}}\:\:{and}\:\:\alpha_{{k}} =−\frac{\mathrm{1}}{\mathrm{4}}{arctan}\left(\frac{\mathrm{1}}{\mathrm{2}}\right)\:+\frac{{k}\pi}{\mathrm{2}}\:\:{with}\:{k}\in\left[\left[\mathrm{0},\mathrm{3}\right]\right]\:\:{so}\:{the}\:{roots}\:{of}\:{this} \\ $$$${equation}\:{are}\:{Z}_{{k}} =^{\mathrm{8}} \sqrt{\mathrm{5}}\:{e}^{{i}\left(−\frac{\mathrm{1}}{\mathrm{4}}{arctan}\left(\frac{\mathrm{1}}{\mathrm{2}}\right)+\frac{{k}\pi}{\mathrm{2}}\right)} \:\:{and}\:{k}\in\left[\left[\mathrm{0},\mathrm{3}\right]\right]. \\ $$
Commented by maxmathsup by imad last updated on 29/Dec/18
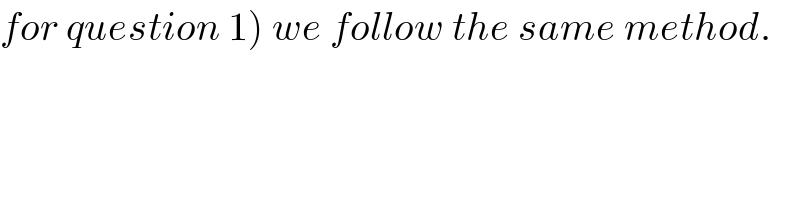
$$\left.{for}\:{question}\:\mathrm{1}\right)\:{we}\:{follow}\:{the}\:{same}\:{method}. \\ $$
Answered by peter frank last updated on 29/Dec/18
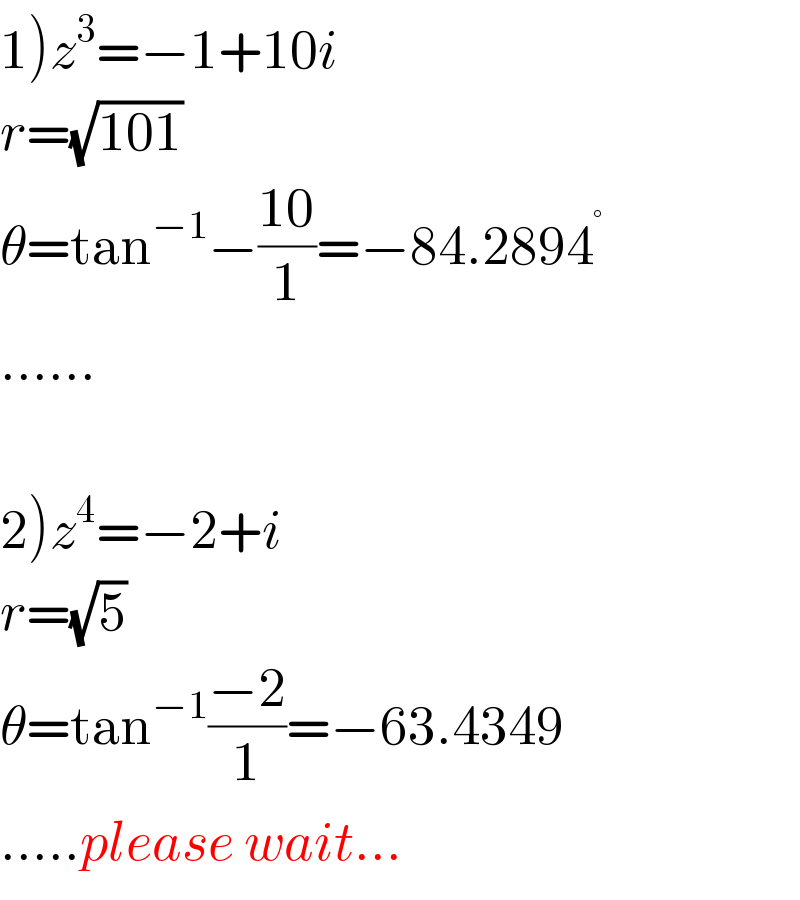
$$\left.\mathrm{1}\right){z}^{\mathrm{3}} =−\mathrm{1}+\mathrm{10}{i} \\ $$$${r}=\sqrt{\mathrm{101}} \\ $$$$\theta=\mathrm{tan}^{−\mathrm{1}} −\frac{\mathrm{10}}{\mathrm{1}}=−\mathrm{84}.\mathrm{2894}^{°} \\ $$$$...... \\ $$$$ \\ $$$$\left.\mathrm{2}\right){z}^{\mathrm{4}} =−\mathrm{2}+{i} \\ $$$${r}=\sqrt{\mathrm{5}} \\ $$$$\theta=\mathrm{tan}^{−\mathrm{1}} \frac{−\mathrm{2}}{\mathrm{1}}=−\mathrm{63}.\mathrm{4349} \\ $$$$.....{please}\:{wait}... \\ $$
Commented by Tawa1 last updated on 29/Dec/18

$$\mathrm{Please}\:\mathrm{is}\:\mathrm{this}\:\mathrm{the}\:\mathrm{solution}\:??? \\ $$
