
Question Number 91000 by niroj last updated on 27/Apr/20
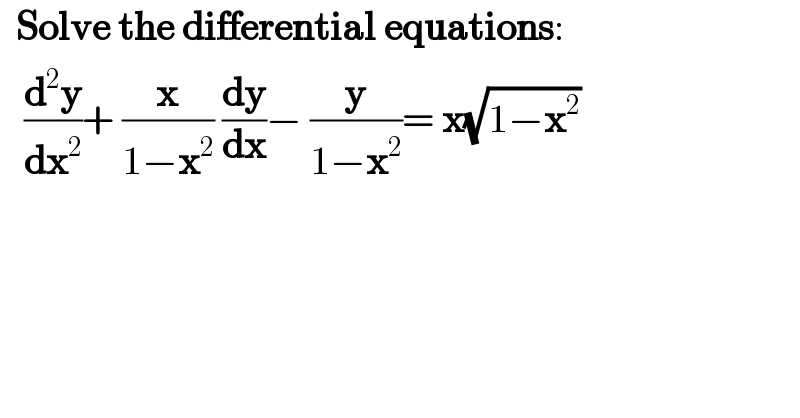
$$\:\:\boldsymbol{\mathrm{Solve}}\:\boldsymbol{\mathrm{the}}\:\boldsymbol{\mathrm{differential}}\:\boldsymbol{\mathrm{equations}}: \\ $$$$\:\:\:\frac{\boldsymbol{\mathrm{d}}^{\mathrm{2}} \boldsymbol{\mathrm{y}}}{\boldsymbol{\mathrm{dx}}^{\mathrm{2}} }+\:\frac{\boldsymbol{\mathrm{x}}}{\mathrm{1}−\boldsymbol{\mathrm{x}}^{\mathrm{2}} }\:\frac{\boldsymbol{\mathrm{dy}}}{\boldsymbol{\mathrm{dx}}}−\:\frac{\boldsymbol{\mathrm{y}}}{\mathrm{1}−\boldsymbol{\mathrm{x}}^{\mathrm{2}} }=\:\boldsymbol{\mathrm{x}}\sqrt{\mathrm{1}−\boldsymbol{\mathrm{x}}^{\mathrm{2}} } \\ $$
Commented by niroj last updated on 27/Apr/20

$$\:{differential}\:{equation}\:{of}\:{variable}\:{coefficients} \\ $$$$\:\:\mathrm{standard}\:\mathrm{form}\:\frac{\mathrm{d}^{\mathrm{2}} \mathrm{y}}{\mathrm{dx}^{\mathrm{2}} }+\mathrm{P}\frac{\mathrm{dy}}{\mathrm{dx}}+\mathrm{Qy}=\mathrm{R}...\left({i}\right) \\ $$$$\:\left(\mathrm{i}\right).\:\mathrm{known}\:\mathrm{as}\:\mathrm{part}\:\mathrm{of}\:\mathrm{cf} \\ $$$$\:\mathrm{then}\:,\:\mathrm{if}\:\mathrm{P}+\mathrm{Qx}=\mathrm{0}\:,\Rightarrow\mathrm{u}=\mathrm{x}\:...\mathrm{etc} \\ $$$$\:\:\:\:\mathrm{complete}\:\mathrm{solution}:\:\mathrm{y}=\mathrm{vx} \\ $$$$\:\left(\mathrm{ii}\right).\:\frac{\mathrm{d}^{\mathrm{2}} \mathrm{v}}{\mathrm{dx}^{\mathrm{2}} }+\frac{\mathrm{dv}}{\mathrm{dx}}\left(\mathrm{p}+\frac{\mathrm{2}}{\mathrm{u}}\frac{\mathrm{du}}{\mathrm{dx}}\right)\frac{\mathrm{dv}}{\mathrm{dx}}=\:\frac{\mathrm{R}}{\mathrm{u}} \\ $$$$\:\:\left(\mathrm{iii}\right).\mathrm{Solve}\:\mathrm{it}\:\mathrm{and}\:\mathrm{get}\:\mathrm{p}. \\ $$$$\:\:\:\left(\mathrm{iv}\right)\:\mathrm{Get}\:\mathrm{v}\:\mathrm{by}\:\mathrm{integration}\:\mathrm{and}\:\mathrm{then}\:\mathrm{y}\:\mathrm{finally}. \\ $$$$ \\ $$$$ \\ $$
Commented by jagoll last updated on 27/Apr/20
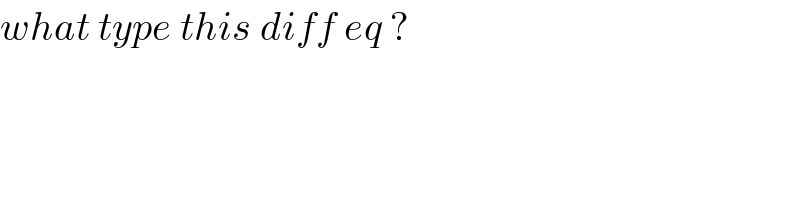
$${what}\:{type}\:{this}\:{diff}\:{eq}\:? \\ $$
