
Previous in Differential Equation Next in Differential Equation
Question Number 12245 by tawa last updated on 16/Apr/17
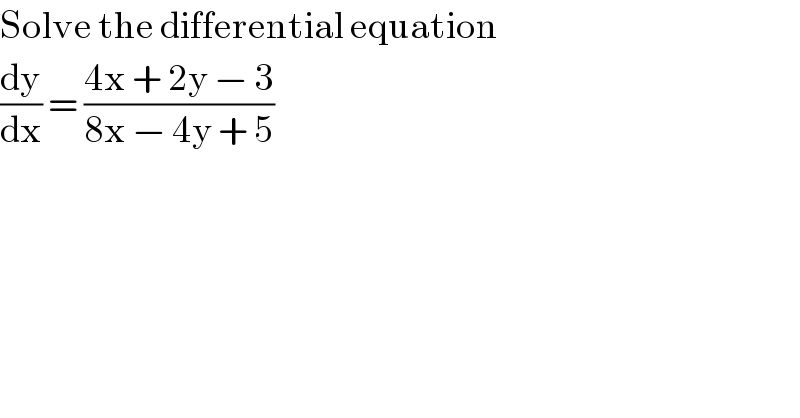
$$\mathrm{Solve}\:\mathrm{the}\:\mathrm{differential}\:\mathrm{equation} \\ $$$$\frac{\mathrm{dy}}{\mathrm{dx}}\:=\:\frac{\mathrm{4x}\:+\:\mathrm{2y}\:−\:\mathrm{3}}{\mathrm{8x}\:−\:\mathrm{4y}\:+\:\mathrm{5}} \\ $$
Answered by mrW1 last updated on 17/Apr/17
![(dy/dx) = ((4x + 2y − 3)/(8x − 4y + 5)) let y=u−p let x=v−q with p,q=constants dy=du dx=dv 4(v−q)+2(u−p)−3=4v+2u+(−4q−2p−3) 8(v−q)−4(u−p)+5=8v−4u+(−8q+4p+5) −4q−2p−3=0 (i) −8q+4p+5=0 (ii) (ii)−(i)×2: 8p+11=0 ⇒p=−((11)/8) (ii)+(i)×2: −16q−1=0 ⇒q=−(1/(16)) (dy/dx) = ((4x + 2y − 3)/(8x − 4y + 5)) ⇒ (du/dv) = ((4v + 2u)/(8v − 4u)) let u=wv (du/dv)=w+v(dw/dv) (du/dv) = ((4v + 2u)/(8v − 4u))⇒ w+v(dw/dv)=((4+2w)/(8−4w))=((2+w)/(4−2w)) v(dw/dv)=((2+w)/(4−2w))−w=((2−3w+2w^2 )/(4−2w)) ((2−w)/(2w^2 −3w+2))dw=(1/(2v))dv ∫((2−w)/(2w^2 −3w+2))dw=∫(1/(2v))dv 2∫(1/(2w^2 −3w+2))dw−∫(w/(2w^2 −3w+2))dw=(1/2)ln v+C (√(4×2×2−9))=(√7) ∫(1/(2w^2 −3w+2))dw=(2/(√7))tan^(−1) (((4w−3)/(√7))) ∫(w/(2w^2 −3w+2))dw=(1/4)ln (2w^2 −3w+2)+(3/(2(√7)))tan^(−1) (((4w−3)/(√7))) (5/(2(√7)))tan^(−1) (((4w−3)/(√7)))−(1/4)ln (2w^2 −3w+2)=(1/2)ln v+C (5/(√7))tan^(−1) (((4w−3)/(√7)))−(1/2)ln (2w^2 −3w+2)=ln v+C (5/(√7))tan^(−1) (((4u−3v)/((√7)v)))−(1/2)ln [2((u/v))^2 −3((u/v))+2]=ln v+C (5/(√7))tan^(−1) [((4(y−((11)/8))−3(x−(1/(16))))/((√7)(x−(1/(16)))))]−(1/2)ln [2(((y−((11)/8))/(x−(1/(16)))))^2 −3(((y−((11)/8))/(x−(1/(16)))))+2]=ln (x−(1/(16)))+C (5/(√7))tan^(−1) [((4(16y−22)−3(16x−1))/((√7)(16x−1)))]−(1/2)ln [2(((16y−22)/(16x−1)))^2 −3(((16y−22)/(16x−1)))+2]=ln (((16x−1)/(16)))+C (5/(√7))tan^(−1) [((64y−48x−85)/((√7)(16x−1)))]−(1/2)ln [8(((8y−11)/(16x−1)))^2 −6(((8y−11)/(16x−1)))+2]=ln (((16x−1)/(16)))+C](Q12281.png)
$$\frac{\mathrm{dy}}{\mathrm{dx}}\:=\:\frac{\mathrm{4x}\:+\:\mathrm{2y}\:−\:\mathrm{3}}{\mathrm{8x}\:−\:\mathrm{4y}\:+\:\mathrm{5}} \\ $$$$ \\ $$$${let}\:{y}={u}−{p} \\ $$$${let}\:{x}={v}−{q} \\ $$$${with}\:{p},{q}={constants} \\ $$$${dy}={du} \\ $$$${dx}={dv} \\ $$$$\mathrm{4}\left({v}−{q}\right)+\mathrm{2}\left({u}−{p}\right)−\mathrm{3}=\mathrm{4}{v}+\mathrm{2}{u}+\left(−\mathrm{4}{q}−\mathrm{2}{p}−\mathrm{3}\right) \\ $$$$\mathrm{8}\left({v}−{q}\right)−\mathrm{4}\left({u}−{p}\right)+\mathrm{5}=\mathrm{8}{v}−\mathrm{4}{u}+\left(−\mathrm{8}{q}+\mathrm{4}{p}+\mathrm{5}\right) \\ $$$$ \\ $$$$−\mathrm{4}{q}−\mathrm{2}{p}−\mathrm{3}=\mathrm{0}\:\:\:\left({i}\right) \\ $$$$−\mathrm{8}{q}+\mathrm{4}{p}+\mathrm{5}=\mathrm{0}\:\:\:\:\left({ii}\right) \\ $$$$\left({ii}\right)−\left({i}\right)×\mathrm{2}: \\ $$$$\mathrm{8}{p}+\mathrm{11}=\mathrm{0} \\ $$$$\Rightarrow{p}=−\frac{\mathrm{11}}{\mathrm{8}} \\ $$$$\left({ii}\right)+\left({i}\right)×\mathrm{2}: \\ $$$$−\mathrm{16}{q}−\mathrm{1}=\mathrm{0} \\ $$$$\Rightarrow{q}=−\frac{\mathrm{1}}{\mathrm{16}} \\ $$$$ \\ $$$$\frac{\mathrm{dy}}{\mathrm{dx}}\:=\:\frac{\mathrm{4x}\:+\:\mathrm{2y}\:−\:\mathrm{3}}{\mathrm{8x}\:−\:\mathrm{4y}\:+\:\mathrm{5}}\:\Rightarrow \\ $$$$\frac{\mathrm{d}{u}}{\mathrm{d}{v}}\:=\:\frac{\mathrm{4}{v}\:+\:\mathrm{2}{u}}{\mathrm{8}{v}\:−\:\mathrm{4}{u}} \\ $$$${let}\:{u}={wv} \\ $$$$\frac{{du}}{{dv}}={w}+{v}\frac{{dw}}{{dv}} \\ $$$$ \\ $$$$\frac{\mathrm{d}{u}}{\mathrm{d}{v}}\:=\:\frac{\mathrm{4}{v}\:+\:\mathrm{2}{u}}{\mathrm{8}{v}\:−\:\mathrm{4}{u}}\Rightarrow \\ $$$${w}+{v}\frac{{dw}}{{dv}}=\frac{\mathrm{4}+\mathrm{2}{w}}{\mathrm{8}−\mathrm{4}{w}}=\frac{\mathrm{2}+{w}}{\mathrm{4}−\mathrm{2}{w}} \\ $$$${v}\frac{{dw}}{{dv}}=\frac{\mathrm{2}+{w}}{\mathrm{4}−\mathrm{2}{w}}−{w}=\frac{\mathrm{2}−\mathrm{3}{w}+\mathrm{2}{w}^{\mathrm{2}} }{\mathrm{4}−\mathrm{2}{w}} \\ $$$$\frac{\mathrm{2}−{w}}{\mathrm{2}{w}^{\mathrm{2}} −\mathrm{3}{w}+\mathrm{2}}{dw}=\frac{\mathrm{1}}{\mathrm{2}{v}}{dv} \\ $$$$\int\frac{\mathrm{2}−{w}}{\mathrm{2}{w}^{\mathrm{2}} −\mathrm{3}{w}+\mathrm{2}}{dw}=\int\frac{\mathrm{1}}{\mathrm{2}{v}}{dv} \\ $$$$\mathrm{2}\int\frac{\mathrm{1}}{\mathrm{2}{w}^{\mathrm{2}} −\mathrm{3}{w}+\mathrm{2}}{dw}−\int\frac{{w}}{\mathrm{2}{w}^{\mathrm{2}} −\mathrm{3}{w}+\mathrm{2}}{dw}=\frac{\mathrm{1}}{\mathrm{2}}\mathrm{ln}\:{v}+{C} \\ $$$$\sqrt{\mathrm{4}×\mathrm{2}×\mathrm{2}−\mathrm{9}}=\sqrt{\mathrm{7}} \\ $$$$\int\frac{\mathrm{1}}{\mathrm{2}{w}^{\mathrm{2}} −\mathrm{3}{w}+\mathrm{2}}{dw}=\frac{\mathrm{2}}{\sqrt{\mathrm{7}}}\mathrm{tan}^{−\mathrm{1}} \left(\frac{\mathrm{4}{w}−\mathrm{3}}{\sqrt{\mathrm{7}}}\right) \\ $$$$\int\frac{{w}}{\mathrm{2}{w}^{\mathrm{2}} −\mathrm{3}{w}+\mathrm{2}}{dw}=\frac{\mathrm{1}}{\mathrm{4}}\mathrm{ln}\:\left(\mathrm{2}{w}^{\mathrm{2}} −\mathrm{3}{w}+\mathrm{2}\right)+\frac{\mathrm{3}}{\mathrm{2}\sqrt{\mathrm{7}}}\mathrm{tan}^{−\mathrm{1}} \left(\frac{\mathrm{4}{w}−\mathrm{3}}{\sqrt{\mathrm{7}}}\right) \\ $$$$ \\ $$$$\frac{\mathrm{5}}{\mathrm{2}\sqrt{\mathrm{7}}}\mathrm{tan}^{−\mathrm{1}} \left(\frac{\mathrm{4}{w}−\mathrm{3}}{\sqrt{\mathrm{7}}}\right)−\frac{\mathrm{1}}{\mathrm{4}}\mathrm{ln}\:\left(\mathrm{2}{w}^{\mathrm{2}} −\mathrm{3}{w}+\mathrm{2}\right)=\frac{\mathrm{1}}{\mathrm{2}}\mathrm{ln}\:{v}+{C} \\ $$$$\frac{\mathrm{5}}{\sqrt{\mathrm{7}}}\mathrm{tan}^{−\mathrm{1}} \left(\frac{\mathrm{4}{w}−\mathrm{3}}{\sqrt{\mathrm{7}}}\right)−\frac{\mathrm{1}}{\mathrm{2}}\mathrm{ln}\:\left(\mathrm{2}{w}^{\mathrm{2}} −\mathrm{3}{w}+\mathrm{2}\right)=\mathrm{ln}\:{v}+{C} \\ $$$$\frac{\mathrm{5}}{\sqrt{\mathrm{7}}}\mathrm{tan}^{−\mathrm{1}} \left(\frac{\mathrm{4}{u}−\mathrm{3}{v}}{\sqrt{\mathrm{7}}{v}}\right)−\frac{\mathrm{1}}{\mathrm{2}}\mathrm{ln}\:\left[\mathrm{2}\left(\frac{{u}}{{v}}\right)^{\mathrm{2}} −\mathrm{3}\left(\frac{{u}}{{v}}\right)+\mathrm{2}\right]=\mathrm{ln}\:{v}+{C} \\ $$$$\frac{\mathrm{5}}{\sqrt{\mathrm{7}}}\mathrm{tan}^{−\mathrm{1}} \left[\frac{\mathrm{4}\left({y}−\frac{\mathrm{11}}{\mathrm{8}}\right)−\mathrm{3}\left({x}−\frac{\mathrm{1}}{\mathrm{16}}\right)}{\sqrt{\mathrm{7}}\left({x}−\frac{\mathrm{1}}{\mathrm{16}}\right)}\right]−\frac{\mathrm{1}}{\mathrm{2}}\mathrm{ln}\:\left[\mathrm{2}\left(\frac{{y}−\frac{\mathrm{11}}{\mathrm{8}}}{{x}−\frac{\mathrm{1}}{\mathrm{16}}}\right)^{\mathrm{2}} −\mathrm{3}\left(\frac{{y}−\frac{\mathrm{11}}{\mathrm{8}}}{{x}−\frac{\mathrm{1}}{\mathrm{16}}}\right)+\mathrm{2}\right]=\mathrm{ln}\:\left({x}−\frac{\mathrm{1}}{\mathrm{16}}\right)+{C} \\ $$$$\frac{\mathrm{5}}{\sqrt{\mathrm{7}}}\mathrm{tan}^{−\mathrm{1}} \left[\frac{\mathrm{4}\left(\mathrm{16}{y}−\mathrm{22}\right)−\mathrm{3}\left(\mathrm{16}{x}−\mathrm{1}\right)}{\sqrt{\mathrm{7}}\left(\mathrm{16}{x}−\mathrm{1}\right)}\right]−\frac{\mathrm{1}}{\mathrm{2}}\mathrm{ln}\:\left[\mathrm{2}\left(\frac{\mathrm{16}{y}−\mathrm{22}}{\mathrm{16}{x}−\mathrm{1}}\right)^{\mathrm{2}} −\mathrm{3}\left(\frac{\mathrm{16}{y}−\mathrm{22}}{\mathrm{16}{x}−\mathrm{1}}\right)+\mathrm{2}\right]=\mathrm{ln}\:\left(\frac{\mathrm{16}{x}−\mathrm{1}}{\mathrm{16}}\right)+{C} \\ $$$$\frac{\mathrm{5}}{\sqrt{\mathrm{7}}}\mathrm{tan}^{−\mathrm{1}} \left[\frac{\mathrm{64}{y}−\mathrm{48}{x}−\mathrm{85}}{\sqrt{\mathrm{7}}\left(\mathrm{16}{x}−\mathrm{1}\right)}\right]−\frac{\mathrm{1}}{\mathrm{2}}\mathrm{ln}\:\left[\mathrm{8}\left(\frac{\mathrm{8}{y}−\mathrm{11}}{\mathrm{16}{x}−\mathrm{1}}\right)^{\mathrm{2}} −\mathrm{6}\left(\frac{\mathrm{8}{y}−\mathrm{11}}{\mathrm{16}{x}−\mathrm{1}}\right)+\mathrm{2}\right]=\mathrm{ln}\:\left(\frac{\mathrm{16}{x}−\mathrm{1}}{\mathrm{16}}\right)+{C} \\ $$
Commented by tawa last updated on 17/Apr/17
$$\mathrm{Wow},\:\mathrm{God}\:\mathrm{bless}\:\mathrm{you}\:\mathrm{sir}.\:\mathrm{I}\:\mathrm{really}\:\mathrm{appreciate}\:\mathrm{sir}. \\ $$
