
Question Number 175746 by Mastermind last updated on 06/Sep/22
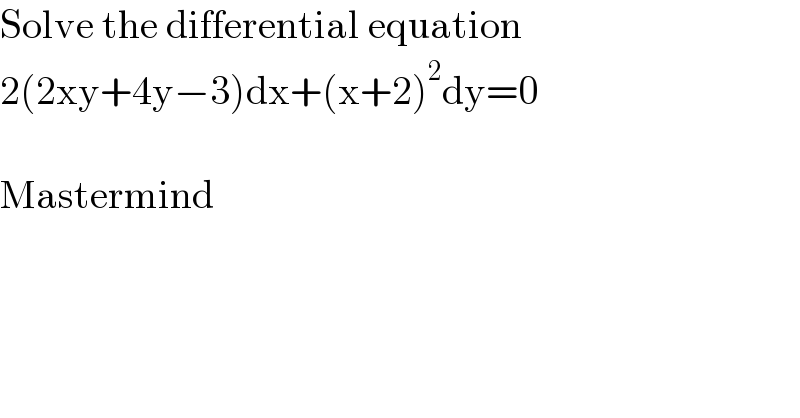
$$\mathrm{Solve}\:\mathrm{the}\:\mathrm{differential}\:\mathrm{equation} \\ $$$$\mathrm{2}\left(\mathrm{2xy}+\mathrm{4y}−\mathrm{3}\right)\mathrm{dx}+\left(\mathrm{x}+\mathrm{2}\right)^{\mathrm{2}} \mathrm{dy}=\mathrm{0} \\ $$$$ \\ $$$$\mathrm{Mastermind} \\ $$
Answered by floor(10²Eta[1]) last updated on 06/Sep/22
![2(2xy+4y−3)+(x+2)^2 (dy/dx)=0 (dy/dx)(x+2)^2 +4y(x+2)−6=0 (dy/dx)+((4y)/((x+2)))=(6/((x+2)^2 )) multipling both sides by e^(∫(4/(x+2))dx) [(dy/dx)+((4y)/(x+2))]e^(4ln(x+2)) =(6/((x+2)^2 ))e^(4ln(x+2)) (dy/dx)e^(4ln(x+2)) +((4y)/(x+2))e^(4ln(x+2)) =(6/((x+2)^2 ))e^(4ln(x+2)) [ye^(4ln(x+2)) ]^′ =(6/((x+2)^2 ))e^(4ln(x+2)) ⇒[y(x+2)^4 ]′=6(x+2)^2 y(x+2)^4 =∫6(x+2)^2 dx y(x+2)^4 =(x^3 /2)+12x^2 +24x+C ⇒y=(x^3 /(2(x+2)^4 ))+((12x^2 +24x+C)/((x+2)^4 ))](Q175757.png)
$$\mathrm{2}\left(\mathrm{2xy}+\mathrm{4y}−\mathrm{3}\right)+\left(\mathrm{x}+\mathrm{2}\right)^{\mathrm{2}} \frac{\mathrm{dy}}{\mathrm{dx}}=\mathrm{0} \\ $$$$\frac{\mathrm{dy}}{\mathrm{dx}}\left(\mathrm{x}+\mathrm{2}\right)^{\mathrm{2}} +\mathrm{4y}\left(\mathrm{x}+\mathrm{2}\right)−\mathrm{6}=\mathrm{0} \\ $$$$\frac{\mathrm{dy}}{\mathrm{dx}}+\frac{\mathrm{4y}}{\left(\mathrm{x}+\mathrm{2}\right)}=\frac{\mathrm{6}}{\left(\mathrm{x}+\mathrm{2}\right)^{\mathrm{2}} } \\ $$$$\mathrm{multipling}\:\mathrm{both}\:\mathrm{sides}\:\mathrm{by}\:\mathrm{e}^{\int\frac{\mathrm{4}}{\mathrm{x}+\mathrm{2}}\mathrm{dx}} \\ $$$$\left[\frac{\mathrm{dy}}{\mathrm{dx}}+\frac{\mathrm{4y}}{\mathrm{x}+\mathrm{2}}\right]\mathrm{e}^{\mathrm{4ln}\left(\mathrm{x}+\mathrm{2}\right)} =\frac{\mathrm{6}}{\left(\mathrm{x}+\mathrm{2}\right)^{\mathrm{2}} }\mathrm{e}^{\mathrm{4ln}\left(\mathrm{x}+\mathrm{2}\right)} \\ $$$$\frac{\mathrm{dy}}{\mathrm{dx}}\mathrm{e}^{\mathrm{4ln}\left(\mathrm{x}+\mathrm{2}\right)} +\frac{\mathrm{4y}}{\mathrm{x}+\mathrm{2}}\mathrm{e}^{\mathrm{4ln}\left(\mathrm{x}+\mathrm{2}\right)} =\frac{\mathrm{6}}{\left(\mathrm{x}+\mathrm{2}\right)^{\mathrm{2}} }\mathrm{e}^{\mathrm{4ln}\left(\mathrm{x}+\mathrm{2}\right)} \\ $$$$\left[\mathrm{ye}^{\mathrm{4ln}\left(\mathrm{x}+\mathrm{2}\right)} \right]^{'} =\frac{\mathrm{6}}{\left(\mathrm{x}+\mathrm{2}\right)^{\mathrm{2}} }\mathrm{e}^{\mathrm{4ln}\left(\mathrm{x}+\mathrm{2}\right)} \\ $$$$\Rightarrow\left[\mathrm{y}\left(\mathrm{x}+\mathrm{2}\right)^{\mathrm{4}} \right]'=\mathrm{6}\left(\mathrm{x}+\mathrm{2}\right)^{\mathrm{2}} \\ $$$$\mathrm{y}\left(\mathrm{x}+\mathrm{2}\right)^{\mathrm{4}} =\int\mathrm{6}\left(\mathrm{x}+\mathrm{2}\right)^{\mathrm{2}} \mathrm{dx} \\ $$$$\mathrm{y}\left(\mathrm{x}+\mathrm{2}\right)^{\mathrm{4}} =\frac{\mathrm{x}^{\mathrm{3}} }{\mathrm{2}}+\mathrm{12x}^{\mathrm{2}} +\mathrm{24x}+\mathrm{C} \\ $$$$\Rightarrow\mathrm{y}=\frac{\mathrm{x}^{\mathrm{3}} }{\mathrm{2}\left(\mathrm{x}+\mathrm{2}\right)^{\mathrm{4}} }+\frac{\mathrm{12x}^{\mathrm{2}} +\mathrm{24x}+\mathrm{C}}{\left(\mathrm{x}+\mathrm{2}\right)^{\mathrm{4}} } \\ $$$$ \\ $$
Commented by Mastermind last updated on 06/Sep/22

$$\mathrm{Thank}\:\mathrm{you}\:\mathrm{man} \\ $$
