
Question Number 183209 by Mastermind last updated on 23/Dec/22
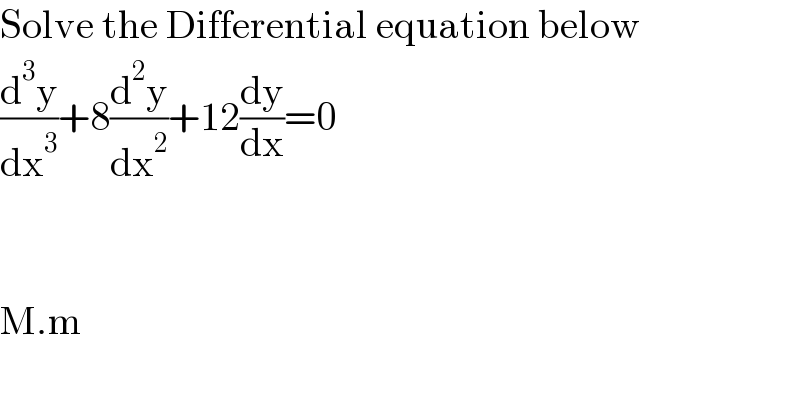
$$\mathrm{Solve}\:\mathrm{the}\:\mathrm{Differential}\:\mathrm{equation}\:\mathrm{below} \\ $$$$\frac{\mathrm{d}^{\mathrm{3}} \mathrm{y}}{\mathrm{dx}^{\mathrm{3}} }+\mathrm{8}\frac{\mathrm{d}^{\mathrm{2}} \mathrm{y}}{\mathrm{dx}^{\mathrm{2}} }+\mathrm{12}\frac{\mathrm{dy}}{\mathrm{dx}}=\mathrm{0} \\ $$$$ \\ $$$$ \\ $$$$\mathrm{M}.\mathrm{m} \\ $$
Answered by aleks041103 last updated on 24/Dec/22
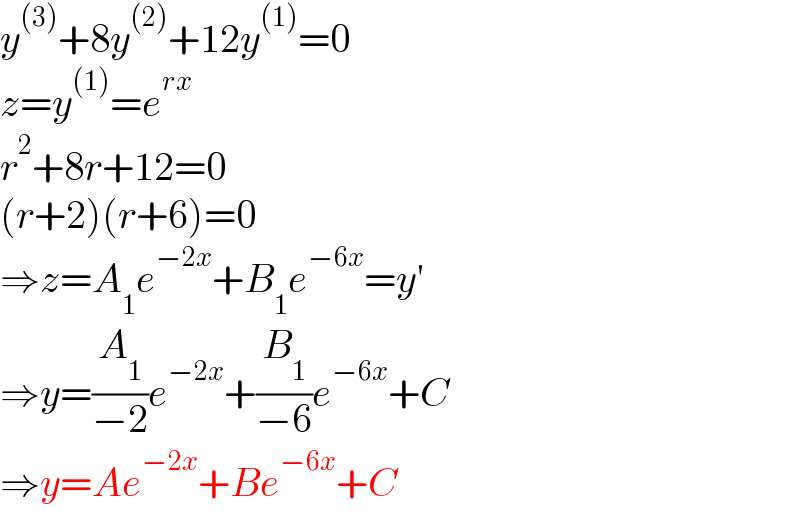
$${y}^{\left(\mathrm{3}\right)} +\mathrm{8}{y}^{\left(\mathrm{2}\right)} +\mathrm{12}{y}^{\left(\mathrm{1}\right)} =\mathrm{0} \\ $$$${z}={y}^{\left(\mathrm{1}\right)} ={e}^{{rx}} \\ $$$${r}^{\mathrm{2}} +\mathrm{8}{r}+\mathrm{12}=\mathrm{0} \\ $$$$\left({r}+\mathrm{2}\right)\left({r}+\mathrm{6}\right)=\mathrm{0} \\ $$$$\Rightarrow{z}={A}_{\mathrm{1}} {e}^{−\mathrm{2}{x}} +{B}_{\mathrm{1}} {e}^{−\mathrm{6}{x}} ={y}' \\ $$$$\Rightarrow{y}=\frac{{A}_{\mathrm{1}} }{−\mathrm{2}}{e}^{−\mathrm{2}{x}} +\frac{{B}_{\mathrm{1}} }{−\mathrm{6}}{e}^{−\mathrm{6}{x}} +{C} \\ $$$$\Rightarrow{y}={Ae}^{−\mathrm{2}{x}} +{Be}^{−\mathrm{6}{x}} +{C} \\ $$
Commented by Mastermind last updated on 23/Dec/22

$$\mathrm{There}\:\mathrm{was}\:\mathrm{an}\:\mathrm{error}\:\mathrm{in}\:\mathrm{the}\:\mathrm{question}, \\ $$$$\mathrm{i}'\mathrm{m}\:\mathrm{sorry} \\ $$$$\mathrm{i}\:\mathrm{have}\:\mathrm{corrected}\:\mathrm{it}\:\mathrm{tho}. \\ $$
Commented by aleks041103 last updated on 24/Dec/22

$${I}\:'{ve}\:{corrected}\:{my}\:{answer}\:{also} \\ $$
Commented by Mastermind last updated on 27/Dec/22
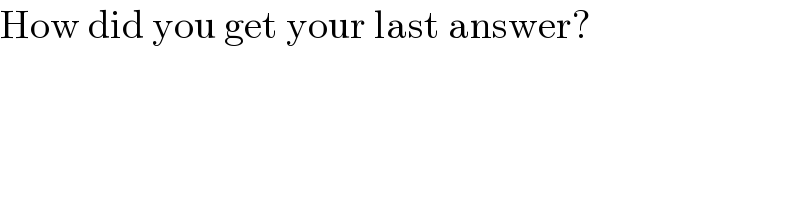
$$\mathrm{How}\:\mathrm{did}\:\mathrm{you}\:\mathrm{get}\:\mathrm{your}\:\mathrm{last}\:\mathrm{answer}? \\ $$
