
Question Number 181219 by Mastermind last updated on 23/Nov/22
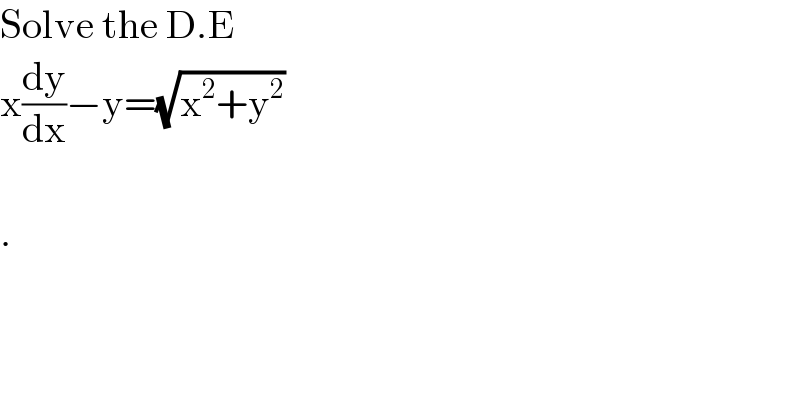
$$\mathrm{Solve}\:\mathrm{the}\:\mathrm{D}.\mathrm{E} \\ $$$$\mathrm{x}\frac{\mathrm{dy}}{\mathrm{dx}}−\mathrm{y}=\sqrt{\mathrm{x}^{\mathrm{2}} +\mathrm{y}^{\mathrm{2}} } \\ $$$$ \\ $$$$. \\ $$
Answered by qaz last updated on 23/Nov/22
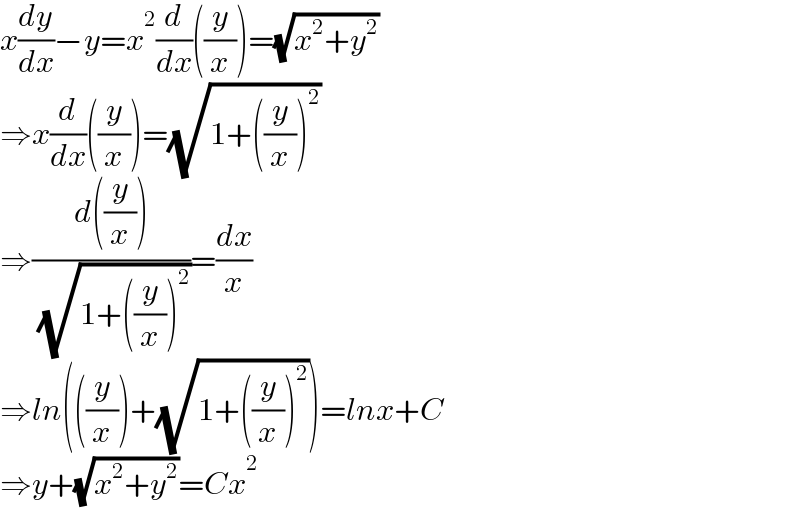
$${x}\frac{{dy}}{{dx}}−{y}={x}^{\mathrm{2}} \frac{{d}}{{dx}}\left(\frac{{y}}{{x}}\right)=\sqrt{{x}^{\mathrm{2}} +{y}^{\mathrm{2}} } \\ $$$$\Rightarrow{x}\frac{{d}}{{dx}}\left(\frac{{y}}{{x}}\right)=\sqrt{\mathrm{1}+\left(\frac{{y}}{{x}}\right)^{\mathrm{2}} } \\ $$$$\Rightarrow\frac{{d}\left(\frac{{y}}{{x}}\right)}{\:\sqrt{\mathrm{1}+\left(\frac{{y}}{{x}}\right)^{\mathrm{2}} }}=\frac{{dx}}{{x}} \\ $$$$\Rightarrow{ln}\left(\left(\frac{{y}}{{x}}\right)+\sqrt{\mathrm{1}+\left(\frac{{y}}{{x}}\right)^{\mathrm{2}} }\right)={lnx}+{C} \\ $$$$\Rightarrow{y}+\sqrt{{x}^{\mathrm{2}} +{y}^{\mathrm{2}} }={Cx}^{\mathrm{2}} \\ $$
Commented by Mastermind last updated on 29/Nov/22
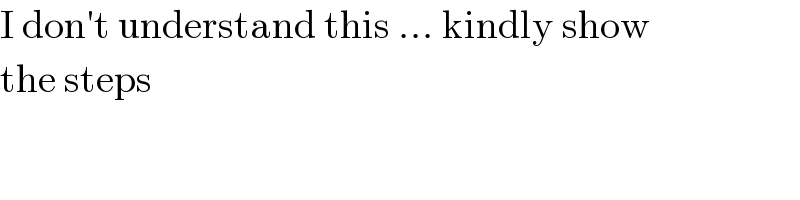
$$\mathrm{I}\:\mathrm{don}'\mathrm{t}\:\mathrm{understand}\:\mathrm{this}\:...\:\mathrm{kindly}\:\mathrm{show} \\ $$$$\mathrm{the}\:\mathrm{steps} \\ $$
