Question Number 11714 by Nayon last updated on 30/Mar/17
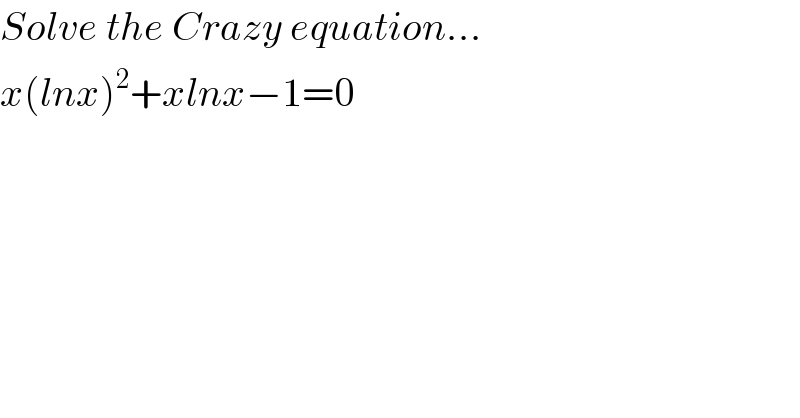
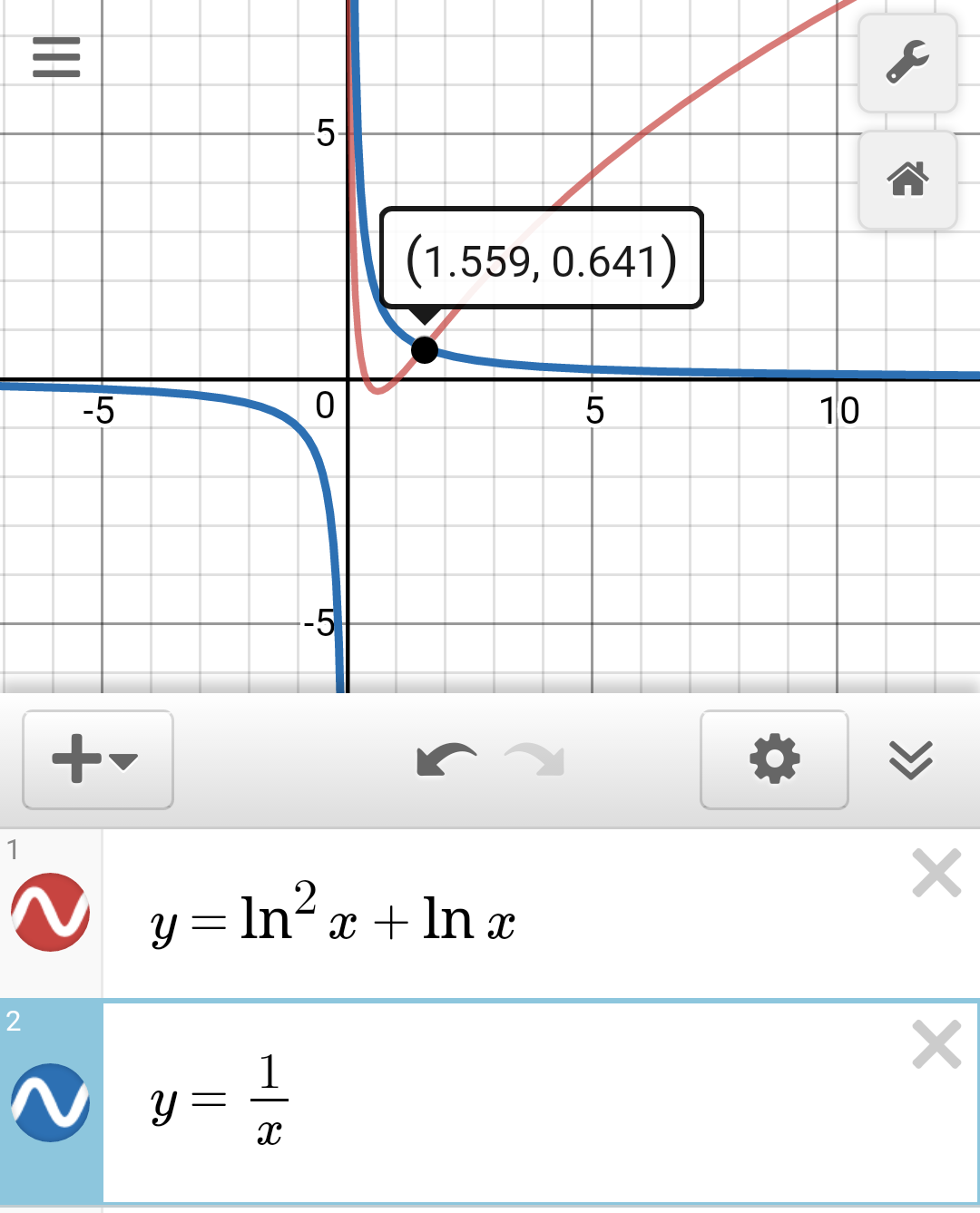
$${Solve}\:{the}\:{Crazy}\:{equation}... \\ $$$${x}\left({lnx}\right)^{\mathrm{2}} +{xlnx}−\mathrm{1}=\mathrm{0} \\ $$
Commented by mrW1 last updated on 30/Mar/17

$$\mathrm{ln}\:{x}=\frac{\sqrt{\mathrm{1}+\frac{\mathrm{4}}{{x}}}−\mathrm{1}}{\mathrm{2}}\:\: \\ $$$${I}\:{don}'{t}\:{think}\:{there}\:{is}\:{an}\:{analytical} \\ $$$${solution}. \\ $$
Commented by FilupS last updated on 31/Mar/17

$${x}\mathrm{ln}^{\mathrm{2}} {x}+{x}\mathrm{ln}{x}=\mathrm{1} \\ $$$${e}^{\mathrm{ln}\left({x}^{{x}\mathrm{ln}{x}} \right)+{x}\mathrm{ln}\left({x}\right)} ={e} \\ $$$${x}\mathrm{ln}{x}={u} \\ $$$${x}={e}^{{W}\left({u}\right)} \:\:\:\:\:\mathrm{product}\:\mathrm{log}\:\mathrm{function} \\ $$$${e}^{{u}\mathrm{ln}\left({e}^{{W}\left({u}\right)} \right)+{u}} ={e} \\ $$$${e}^{{uW}\left({u}\right)+{u}} ={e} \\ $$$${e}^{{u}\left({W}\left({u}\right)+\mathrm{1}\right)} ={e} \\ $$$$\therefore{u}\left({W}\left({u}\right)+\mathrm{1}\right)=\mathrm{1} \\ $$$${W}\left({u}\right)=\frac{\mathrm{1}}{{u}}−\mathrm{1} \\ $$$$\: \\ $$$${A}\mathrm{s}\:\mathrm{said}\:\mathrm{above},\:\mathrm{I}\:\mathrm{am}\:\mathrm{unsure}\:\mathrm{an}\:\mathrm{analytical} \\ $$$$\mathrm{solution}\:\mathrm{exists} \\ $$$$\: \\ $$$${Please}\:{correct}\:{any}\:{mistakes} \\ $$
Commented by b.e.h.i.8.3.4.1.7@gmail.com last updated on 07/Apr/17