
Question Number 131107 by ZiYangLee last updated on 01/Feb/21
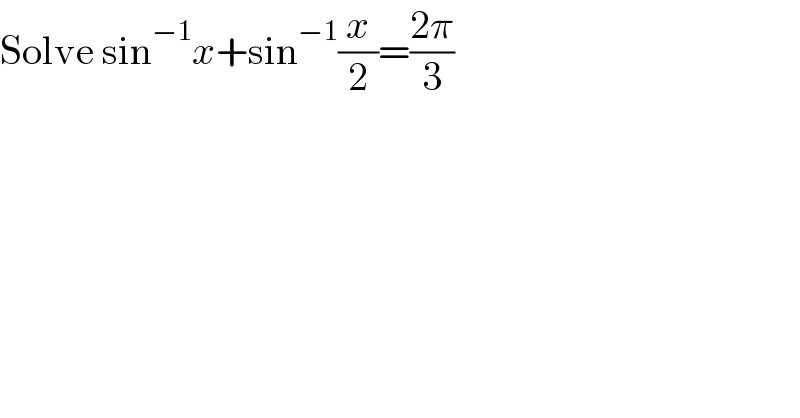
$$\mathrm{Solve}\:\mathrm{sin}^{−\mathrm{1}} {x}+\mathrm{sin}^{−\mathrm{1}} \frac{{x}}{\mathrm{2}}=\frac{\mathrm{2}\pi}{\mathrm{3}} \\ $$
Answered by mr W last updated on 01/Feb/21
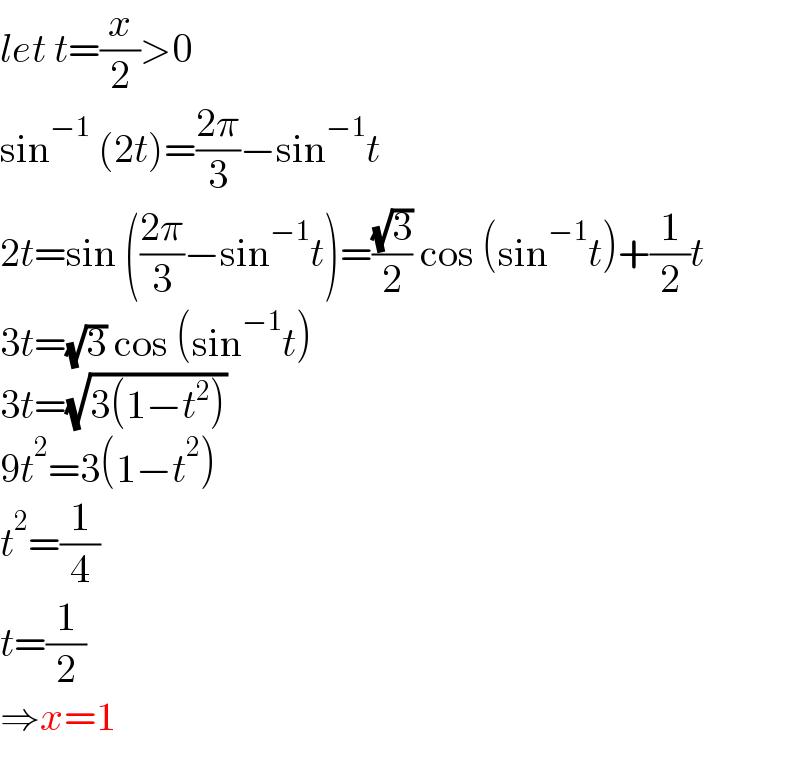
$${let}\:{t}=\frac{{x}}{\mathrm{2}}>\mathrm{0} \\ $$$$\mathrm{sin}^{−\mathrm{1}} \:\left(\mathrm{2}{t}\right)=\frac{\mathrm{2}\pi}{\mathrm{3}}−\mathrm{sin}^{−\mathrm{1}} {t} \\ $$$$\mathrm{2}{t}=\mathrm{sin}\:\left(\frac{\mathrm{2}\pi}{\mathrm{3}}−\mathrm{sin}^{−\mathrm{1}} {t}\right)=\frac{\sqrt{\mathrm{3}}}{\mathrm{2}}\:\mathrm{cos}\:\left(\mathrm{sin}^{−\mathrm{1}} {t}\right)+\frac{\mathrm{1}}{\mathrm{2}}{t} \\ $$$$\mathrm{3}{t}=\sqrt{\mathrm{3}}\:\mathrm{cos}\:\left(\mathrm{sin}^{−\mathrm{1}} {t}\right) \\ $$$$\mathrm{3}{t}=\sqrt{\mathrm{3}\left(\mathrm{1}−{t}^{\mathrm{2}} \right)} \\ $$$$\mathrm{9}{t}^{\mathrm{2}} =\mathrm{3}\left(\mathrm{1}−{t}^{\mathrm{2}} \right) \\ $$$${t}^{\mathrm{2}} =\frac{\mathrm{1}}{\mathrm{4}} \\ $$$${t}=\frac{\mathrm{1}}{\mathrm{2}} \\ $$$$\Rightarrow{x}=\mathrm{1} \\ $$
Answered by EDWIN88 last updated on 02/Feb/21
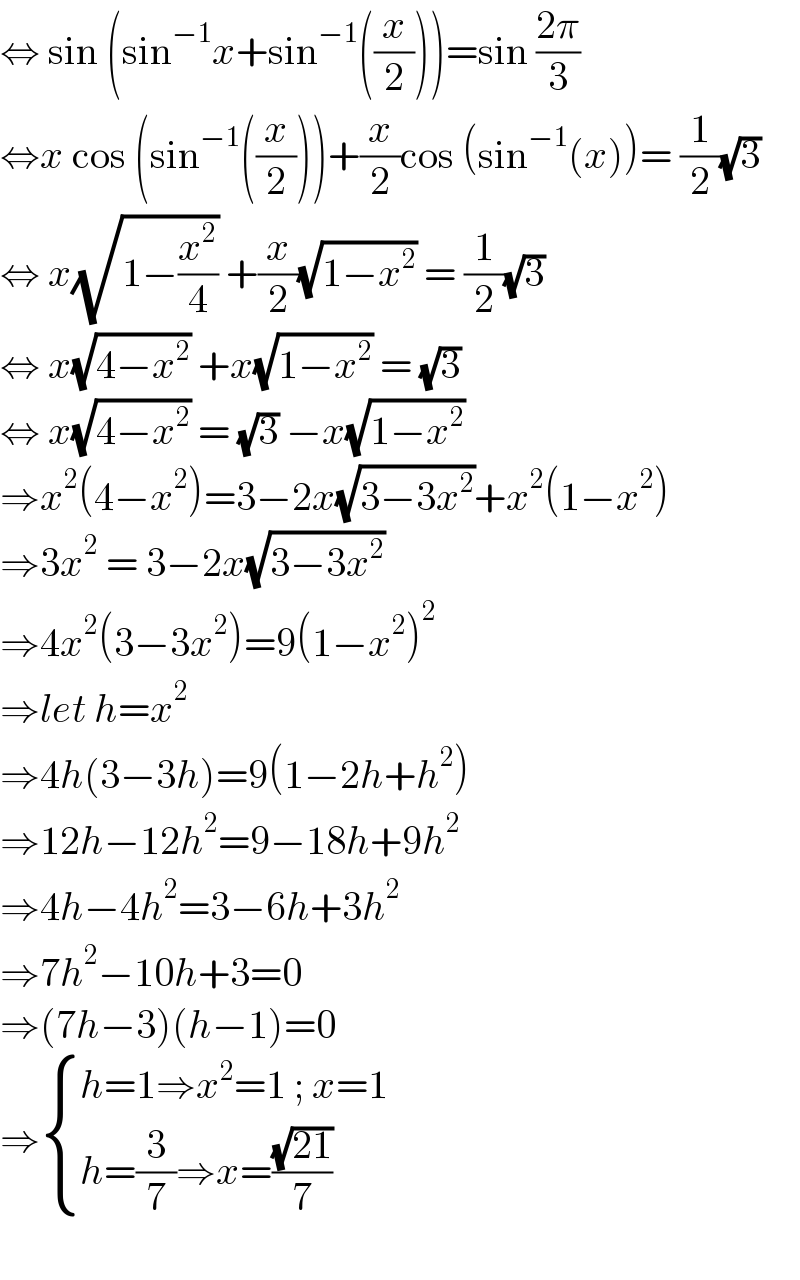
$$\Leftrightarrow\:\mathrm{sin}\:\left(\mathrm{sin}^{−\mathrm{1}} {x}+\mathrm{sin}^{−\mathrm{1}} \left(\frac{{x}}{\mathrm{2}}\right)\right)=\mathrm{sin}\:\frac{\mathrm{2}\pi}{\mathrm{3}} \\ $$$$\Leftrightarrow{x}\:\mathrm{cos}\:\left(\mathrm{sin}^{−\mathrm{1}} \left(\frac{{x}}{\mathrm{2}}\right)\right)+\frac{{x}}{\mathrm{2}}\mathrm{cos}\:\left(\mathrm{sin}^{−\mathrm{1}} \left({x}\right)\right)=\:\frac{\mathrm{1}}{\mathrm{2}}\sqrt{\mathrm{3}} \\ $$$$\Leftrightarrow\:{x}\sqrt{\mathrm{1}−\frac{{x}^{\mathrm{2}} }{\mathrm{4}}}\:+\frac{{x}}{\mathrm{2}}\sqrt{\mathrm{1}−{x}^{\mathrm{2}} }\:=\:\frac{\mathrm{1}}{\mathrm{2}}\sqrt{\mathrm{3}} \\ $$$$\Leftrightarrow\:{x}\sqrt{\mathrm{4}−{x}^{\mathrm{2}} }\:+{x}\sqrt{\mathrm{1}−{x}^{\mathrm{2}} }\:=\:\sqrt{\mathrm{3}} \\ $$$$\Leftrightarrow\:{x}\sqrt{\mathrm{4}−{x}^{\mathrm{2}} }\:=\:\sqrt{\mathrm{3}}\:−{x}\sqrt{\mathrm{1}−{x}^{\mathrm{2}} } \\ $$$$\Rightarrow{x}^{\mathrm{2}} \left(\mathrm{4}−{x}^{\mathrm{2}} \right)=\mathrm{3}−\mathrm{2}{x}\sqrt{\mathrm{3}−\mathrm{3}{x}^{\mathrm{2}} }+{x}^{\mathrm{2}} \left(\mathrm{1}−{x}^{\mathrm{2}} \right) \\ $$$$\Rightarrow\mathrm{3}{x}^{\mathrm{2}} \:=\:\mathrm{3}−\mathrm{2}{x}\sqrt{\mathrm{3}−\mathrm{3}{x}^{\mathrm{2}} } \\ $$$$\Rightarrow\mathrm{4}{x}^{\mathrm{2}} \left(\mathrm{3}−\mathrm{3}{x}^{\mathrm{2}} \right)=\mathrm{9}\left(\mathrm{1}−{x}^{\mathrm{2}} \right)^{\mathrm{2}} \\ $$$$\Rightarrow{let}\:{h}={x}^{\mathrm{2}} \\ $$$$\Rightarrow\mathrm{4}{h}\left(\mathrm{3}−\mathrm{3}{h}\right)=\mathrm{9}\left(\mathrm{1}−\mathrm{2}{h}+{h}^{\mathrm{2}} \right) \\ $$$$\Rightarrow\mathrm{12}{h}−\mathrm{12}{h}^{\mathrm{2}} =\mathrm{9}−\mathrm{18}{h}+\mathrm{9}{h}^{\mathrm{2}} \\ $$$$\Rightarrow\mathrm{4}{h}−\mathrm{4}{h}^{\mathrm{2}} =\mathrm{3}−\mathrm{6}{h}+\mathrm{3}{h}^{\mathrm{2}} \\ $$$$\Rightarrow\mathrm{7}{h}^{\mathrm{2}} −\mathrm{10}{h}+\mathrm{3}=\mathrm{0} \\ $$$$\Rightarrow\left(\mathrm{7}{h}−\mathrm{3}\right)\left({h}−\mathrm{1}\right)=\mathrm{0} \\ $$$$\Rightarrow\begin{cases}{{h}=\mathrm{1}\Rightarrow{x}^{\mathrm{2}} =\mathrm{1}\:;\:{x}=\mathrm{1}}\\{{h}=\frac{\mathrm{3}}{\mathrm{7}}\Rightarrow{x}=\frac{\sqrt{\mathrm{21}}}{\mathrm{7}}\:}\end{cases} \\ $$$$ \\ $$
Commented by mr W last updated on 02/Feb/21
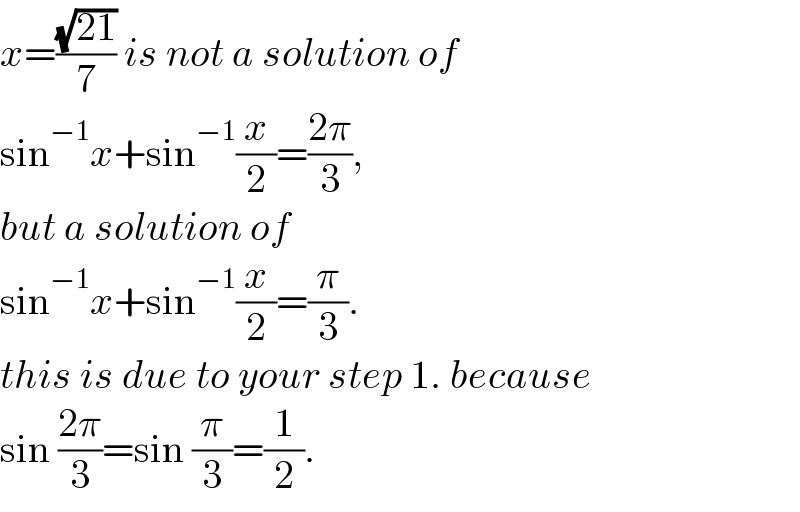
$${x}=\frac{\sqrt{\mathrm{21}}}{\mathrm{7}}\:{is}\:{not}\:{a}\:{solution}\:{of} \\ $$$$\mathrm{sin}^{−\mathrm{1}} {x}+\mathrm{sin}^{−\mathrm{1}} \frac{{x}}{\mathrm{2}}=\frac{\mathrm{2}\pi}{\mathrm{3}}, \\ $$$${but}\:{a}\:{solution}\:{of} \\ $$$$\mathrm{sin}^{−\mathrm{1}} {x}+\mathrm{sin}^{−\mathrm{1}} \frac{{x}}{\mathrm{2}}=\frac{\pi}{\mathrm{3}}. \\ $$$${this}\:{is}\:{due}\:{to}\:{your}\:{step}\:\mathrm{1}.\:{because} \\ $$$$\mathrm{sin}\:\frac{\mathrm{2}\pi}{\mathrm{3}}=\mathrm{sin}\:\frac{\pi}{\mathrm{3}}=\frac{\mathrm{1}}{\mathrm{2}}. \\ $$
