
Question Number 13909 by tawa tawa last updated on 25/May/17
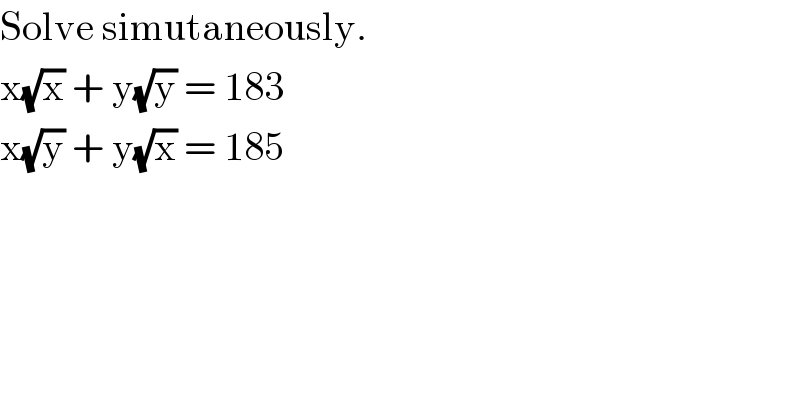
$$\mathrm{Solve}\:\mathrm{simutaneously}. \\ $$$$\mathrm{x}\sqrt{\mathrm{x}}\:+\:\mathrm{y}\sqrt{\mathrm{y}}\:=\:\mathrm{183} \\ $$$$\mathrm{x}\sqrt{\mathrm{y}}\:+\:\mathrm{y}\sqrt{\mathrm{x}}\:=\:\mathrm{185} \\ $$
Commented by RasheedSindhi last updated on 25/May/17
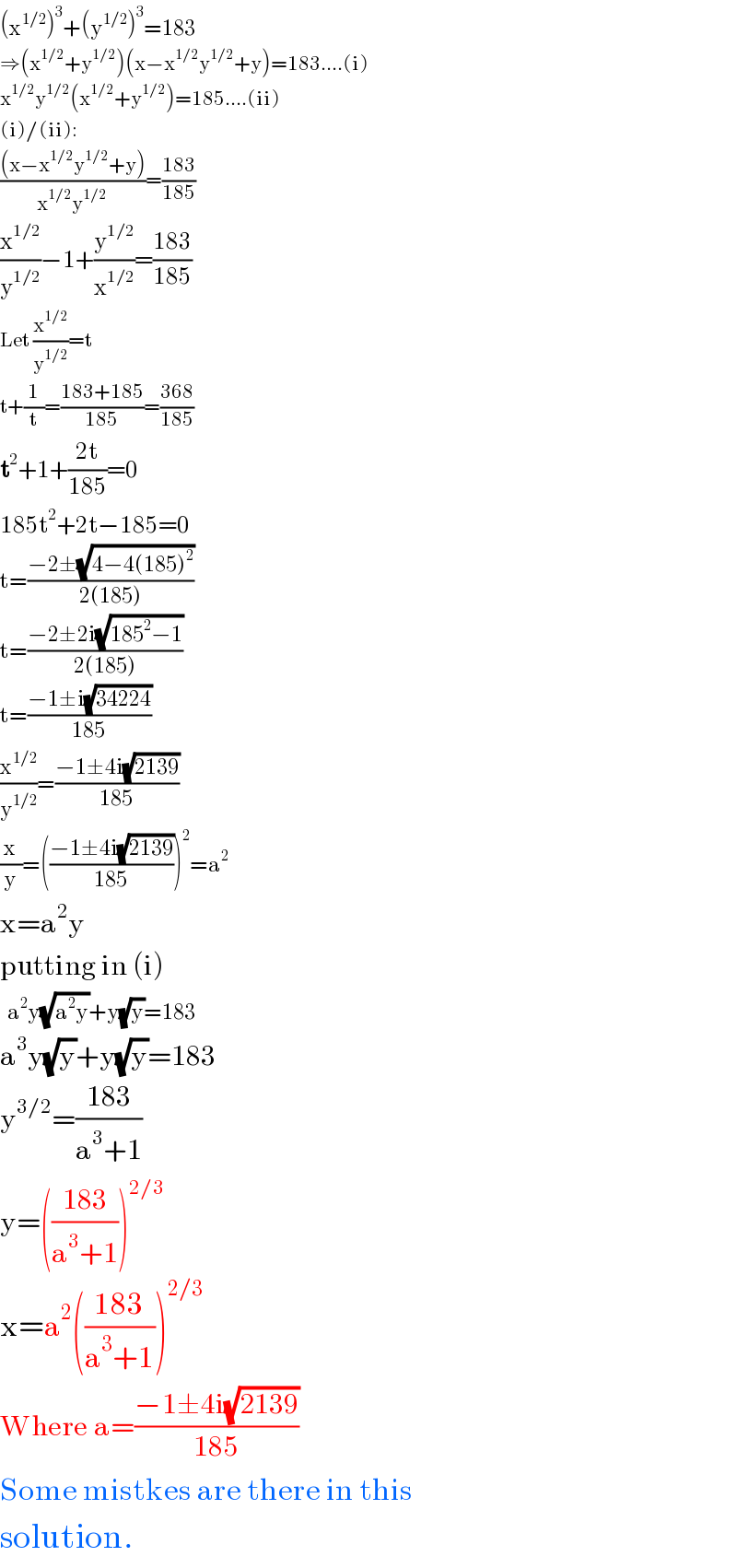
$$\left(\mathrm{x}^{\mathrm{1}/\mathrm{2}} \right)^{\mathrm{3}} +\left(\mathrm{y}^{\mathrm{1}/\mathrm{2}} \right)^{\mathrm{3}} =\mathrm{183} \\ $$$$\Rightarrow\left(\mathrm{x}^{\mathrm{1}/\mathrm{2}} +\mathrm{y}^{\mathrm{1}/\mathrm{2}} \right)\left(\mathrm{x}−\mathrm{x}^{\mathrm{1}/\mathrm{2}} \mathrm{y}^{\mathrm{1}/\mathrm{2}} +\mathrm{y}\right)=\mathrm{183}....\left(\mathrm{i}\right) \\ $$$$\mathrm{x}^{\mathrm{1}/\mathrm{2}} \mathrm{y}^{\mathrm{1}/\mathrm{2}} \left(\mathrm{x}^{\mathrm{1}/\mathrm{2}} +\mathrm{y}^{\mathrm{1}/\mathrm{2}} \right)=\mathrm{185}....\left(\mathrm{ii}\right) \\ $$$$\left(\mathrm{i}\right)/\left(\mathrm{ii}\right): \\ $$$$\frac{\left(\mathrm{x}−\mathrm{x}^{\mathrm{1}/\mathrm{2}} \mathrm{y}^{\mathrm{1}/\mathrm{2}} +\mathrm{y}\right)}{\mathrm{x}^{\mathrm{1}/\mathrm{2}} \mathrm{y}^{\mathrm{1}/\mathrm{2}} }=\frac{\mathrm{183}}{\mathrm{185}} \\ $$$$\frac{\mathrm{x}^{\mathrm{1}/\mathrm{2}} }{\mathrm{y}^{\mathrm{1}/\mathrm{2}} }−\mathrm{1}+\frac{\mathrm{y}^{\mathrm{1}/\mathrm{2}} }{\mathrm{x}^{\mathrm{1}/\mathrm{2}} }=\frac{\mathrm{183}}{\mathrm{185}} \\ $$$$\mathrm{Let}\:\frac{\mathrm{x}^{\mathrm{1}/\mathrm{2}} }{\mathrm{y}^{\mathrm{1}/\mathrm{2}} }=\mathrm{t} \\ $$$$\mathrm{t}+\frac{\mathrm{1}}{\mathrm{t}}=\frac{\mathrm{183}+\mathrm{185}}{\mathrm{185}}=\frac{\mathrm{368}}{\mathrm{185}} \\ $$$$\boldsymbol{\mathrm{t}}^{\mathrm{2}} +\mathrm{1}+\frac{\mathrm{2t}}{\mathrm{185}}=\mathrm{0} \\ $$$$\mathrm{185t}^{\mathrm{2}} +\mathrm{2t}−\mathrm{185}=\mathrm{0} \\ $$$$\mathrm{t}=\frac{−\mathrm{2}\pm\sqrt{\mathrm{4}−\mathrm{4}\left(\mathrm{185}\right)^{\mathrm{2}} }}{\mathrm{2}\left(\mathrm{185}\right)} \\ $$$$\mathrm{t}=\frac{−\mathrm{2}\pm\mathrm{2i}\sqrt{\mathrm{185}^{\mathrm{2}} −\mathrm{1}}}{\mathrm{2}\left(\mathrm{185}\right)} \\ $$$$\mathrm{t}=\frac{−\mathrm{1}\pm\mathrm{i}\sqrt{\mathrm{34224}}}{\mathrm{185}} \\ $$$$\frac{\mathrm{x}^{\mathrm{1}/\mathrm{2}} }{\mathrm{y}^{\mathrm{1}/\mathrm{2}} }=\frac{−\mathrm{1}\pm\mathrm{4i}\sqrt{\mathrm{2139}}}{\mathrm{185}} \\ $$$$\frac{\mathrm{x}}{\mathrm{y}}=\left(\frac{−\mathrm{1}\pm\mathrm{4i}\sqrt{\mathrm{2139}}}{\mathrm{185}}\right)^{\mathrm{2}} =\mathrm{a}^{\mathrm{2}} \\ $$$$\mathrm{x}=\mathrm{a}^{\mathrm{2}} \mathrm{y} \\ $$$$\mathrm{putting}\:\mathrm{in}\:\left(\mathrm{i}\right) \\ $$$$\:\:\mathrm{a}^{\mathrm{2}} \mathrm{y}\sqrt{\mathrm{a}^{\mathrm{2}} \mathrm{y}}+\mathrm{y}\sqrt{\mathrm{y}}=\mathrm{183} \\ $$$$\mathrm{a}^{\mathrm{3}} \mathrm{y}\sqrt{\mathrm{y}}+\mathrm{y}\sqrt{\mathrm{y}}=\mathrm{183} \\ $$$$\mathrm{y}^{\mathrm{3}/\mathrm{2}} =\frac{\mathrm{183}}{\mathrm{a}^{\mathrm{3}} +\mathrm{1}} \\ $$$$\mathrm{y}=\left(\frac{\mathrm{183}}{\mathrm{a}^{\mathrm{3}} +\mathrm{1}}\right)^{\mathrm{2}/\mathrm{3}} \\ $$$$\mathrm{x}=\mathrm{a}^{\mathrm{2}} \left(\frac{\mathrm{183}}{\mathrm{a}^{\mathrm{3}} +\mathrm{1}}\right)^{\mathrm{2}/\mathrm{3}} \\ $$$$\mathrm{Where}\:\mathrm{a}=\frac{−\mathrm{1}\pm\mathrm{4i}\sqrt{\mathrm{2139}}}{\mathrm{185}} \\ $$$$\mathrm{Some}\:\mathrm{mistkes}\:\mathrm{are}\:\mathrm{there}\:\mathrm{in}\:\mathrm{this} \\ $$$$\mathrm{solution}. \\ $$
Commented by ajfour last updated on 25/May/17
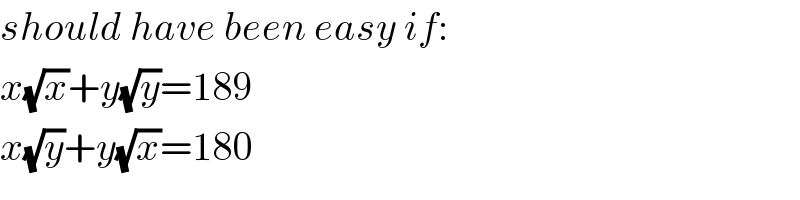
$${should}\:{have}\:{been}\:{easy}\:{if}: \\ $$$${x}\sqrt{{x}}+{y}\sqrt{{y}}=\mathrm{189} \\ $$$${x}\sqrt{{y}}+{y}\sqrt{{x}}=\mathrm{180}\: \\ $$
Commented by mrW1 last updated on 25/May/17

$${You}\:{are}\:{right}.\:{The}\:{given}\:{numbers} \\ $$$${deliver}\:{no}\:{real}\:{solution}\:{and}\:{make} \\ $$$${it}\:{difficult}\:{to}\:{check}\:{the}\:{result}. \\ $$
Commented by ajfour last updated on 25/May/17
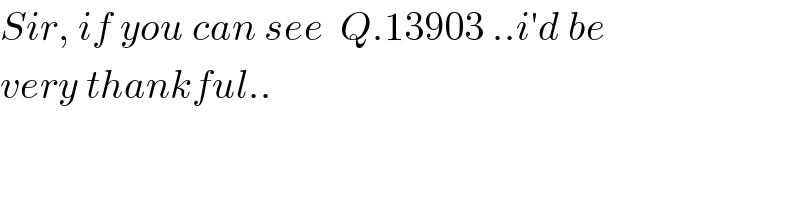
$${Sir},\:{if}\:{you}\:{can}\:{see}\:\:{Q}.\mathrm{13903}\:..{i}'{d}\:{be}\: \\ $$$${very}\:{thankful}.. \\ $$
Commented by tawa tawa last updated on 25/May/17

$$\mathrm{God}\:\mathrm{bless}\:\mathrm{you}\:\mathrm{sir} \\ $$
Answered by mrW1 last updated on 25/May/17

$${u}=\sqrt{{x}} \\ $$$${v}=\sqrt{{y}} \\ $$$${u}^{\mathrm{3}} +{v}^{\mathrm{3}} =\mathrm{183}\:\:\:\left(\mathrm{189}\right) \\ $$$${u}^{\mathrm{2}} {v}+{v}^{\mathrm{2}} {u}=\mathrm{185}\:\:\:\left(\mathrm{180}\right) \\ $$$$\left({u}+{v}\right)^{\mathrm{3}} ={u}^{\mathrm{3}} +{v}^{\mathrm{3}} +\mathrm{3}\left({u}^{\mathrm{2}} {v}+{v}^{\mathrm{2}} {u}\right)=\mathrm{183}+\mathrm{3}×\mathrm{185}=\mathrm{738}\:\:\left(=\mathrm{189}+\mathrm{3}×\mathrm{180}=\mathrm{729}\right) \\ $$$${u}+{v}=\:^{\mathrm{3}} \sqrt{\mathrm{738}}=\mathrm{9}.\mathrm{037}={a}\:\:\left(=\:^{\mathrm{3}} \sqrt{\mathrm{729}}=\mathrm{9}\right) \\ $$$${uv}\left({u}+{v}\right)={uva} \\ $$$${u}^{\mathrm{2}} {v}+{v}^{\mathrm{2}} {u}={uva} \\ $$$$\mathrm{185}={uva}\:\:\:\left(\mathrm{180}=\mathrm{9}{uv}\right) \\ $$$${uv}=\frac{\mathrm{185}}{{a}}=\mathrm{20}.\mathrm{472}={b}\:\:\:\left(=\frac{\mathrm{180}}{\mathrm{9}}=\mathrm{20}\right) \\ $$$$\begin{cases}{{u}+{v}={a}\:\:\left(\mathrm{9}\right)}\\{{uv}={b}\:\:\:\:\left(\mathrm{20}\right)}\end{cases} \\ $$$$\left({u}−{v}\right)^{\mathrm{2}} ={u}^{\mathrm{2}} +{v}^{\mathrm{2}} −\mathrm{2}{uv}={u}^{\mathrm{2}} +{v}^{\mathrm{2}} +\mathrm{2}{uv}−\mathrm{4}{uv} \\ $$$$=\left({u}+{v}\right)^{\mathrm{2}} −\mathrm{4}{uv}={a}^{\mathrm{2}} −\mathrm{4}{b}=−\mathrm{0}.\mathrm{2206}\:\:\left(=\mathrm{9}^{\mathrm{2}} −\mathrm{4}×\mathrm{20}=\mathrm{1}\right) \\ $$$${u}−{v}=\pm\mathrm{0}.\mathrm{47}{i}=\pm{ci}\:\:\left(=\pm\mathrm{1}\right) \\ $$$$\Rightarrow\sqrt{{x}}={u}=\left(\frac{{u}+{v}}{\mathrm{2}}\right)+\left(\frac{{u}−{v}}{\mathrm{2}}\right)=\frac{{a}}{\mathrm{2}}\pm\frac{{c}}{\mathrm{2}}{i}=\mathrm{4}.\mathrm{52}\pm\mathrm{0}.\mathrm{235}{i}\:\:\left(\frac{\mathrm{9}}{\mathrm{2}}\pm\frac{\mathrm{1}}{\mathrm{2}}=\mathrm{5}\:{or}\:\mathrm{4}\right) \\ $$$$\Rightarrow\sqrt{{y}}={v}=\left(\frac{{u}+{v}}{\mathrm{2}}\right)−\left(\frac{{u}−{v}}{\mathrm{2}}\right)=\frac{{a}}{\mathrm{2}}\mp\frac{{c}}{\mathrm{2}}{i}=\mathrm{4}.\mathrm{52}\mp\mathrm{0}.\mathrm{235}{i}\:\:\left(\frac{\mathrm{9}}{\mathrm{2}}\mp\frac{\mathrm{1}}{\mathrm{2}}=\mathrm{4}\:{or}\:\mathrm{5}\right) \\ $$$$\Rightarrow{x}=\left(\mathrm{4}.\mathrm{5}\pm\mathrm{0}.\mathrm{235}{i}\right)^{\mathrm{2}} =\mathrm{20}.\mathrm{375}\pm\mathrm{2}.\mathrm{124}{i}\:\:\left(\mathrm{5}^{\mathrm{2}} =\mathrm{25}\:{or}\:\mathrm{4}^{\mathrm{2}} =\mathrm{16}\right) \\ $$$$\Rightarrow{y}=\left(\mathrm{4}.\mathrm{5}\mp\mathrm{0}.\mathrm{235}{i}\right)^{\mathrm{2}} =\mathrm{20}.\mathrm{375}\mp\mathrm{2}.\mathrm{124}{i}\:\:\left(\mathrm{4}^{\mathrm{2}} =\mathrm{16}\:{or}\:\mathrm{5}^{\mathrm{2}} =\mathrm{25}\right) \\ $$
Commented by RasheedSindhi last updated on 25/May/17

$$\mathcal{V}\:\mathcal{N}{ice}\:\mathcal{S}{ir}! \\ $$
Commented by mrW1 last updated on 25/May/17

$${Thank}\:{you}\:{sir}! \\ $$
Commented by tawa tawa last updated on 25/May/17

$$\mathrm{God}\:\mathrm{bless}\:\mathrm{you}\:\mathrm{sir}. \\ $$
Answered by AH Soomro last updated on 25/May/17

$${A}\:\:{different}\:\:{try} \\ $$$$\mathrm{x}\sqrt{\mathrm{x}}\:+\:\mathrm{y}\sqrt{\mathrm{y}}\:=\:\mathrm{183}..........\left({i}\right) \\ $$$$\mathrm{x}\sqrt{\mathrm{y}}\:+\:\mathrm{y}\sqrt{\mathrm{x}}\:=\:\mathrm{185}..........\left({ii}\right) \\ $$$$ \\ $$$$\left({i}\right)^{\mathrm{2}} −\left({ii}\right)^{\mathrm{2}} : \\ $$$$\:\:\:\:\mathrm{x}^{\mathrm{3}} +\mathrm{2xy}\sqrt{\mathrm{xy}}+\mathrm{y}^{\mathrm{3}} =\mathrm{33489} \\ $$$$\:\:\:\mathrm{x}^{\mathrm{2}} \mathrm{y}+\mathrm{2xy}\sqrt{\mathrm{xy}}+\mathrm{xy}^{\mathrm{2}} =\mathrm{34225} \\ $$$$\:\:\:\mathrm{x}^{\mathrm{3}} +\mathrm{y}^{\mathrm{3}} −\left(\mathrm{x}^{\mathrm{2}} \mathrm{y}+\mathrm{xy}^{\mathrm{2}} \right)=−\mathrm{736} \\ $$$$\:\:\:\:\left(\mathrm{x}+\mathrm{y}\right)\left(\mathrm{x}^{\mathrm{2}} −\mathrm{xy}+\mathrm{y}^{\mathrm{2}} \right)−\mathrm{xy}\left(\mathrm{x}+\mathrm{y}\right)=−\mathrm{736} \\ $$$$\left(\mathrm{x}+\mathrm{y}\right)\left(\mathrm{x}−\mathrm{y}\right)^{\mathrm{2}} =−\mathrm{736} \\ $$$$\mathrm{Continue} \\ $$
Commented by tawa tawa last updated on 25/May/17

$$\mathrm{God}\:\mathrm{bless}\:\mathrm{you}\:\mathrm{sir}. \\ $$
Answered by RasheedSindhi last updated on 25/May/17
![Answer of the modified question. Modification suggested by ajfour. x(√x) + y(√y) = 189...........(i) x(√y) + y(√x) = 180............(ii) (i)⇒x^(3/2) +y^(3/2) =189 ⇒(x^(1/2) +y^(1/2) )(x−x^(1/2) y^(1/2) +y)=189....(iii) (ii)⇒x^(1/2) y^(1/2) (x^(1/2) +y^(1/2) )=180...(iv) (iii)/(iv):((x−x^(1/2) y^(1/2) +y)/(x^(1/2) y^(1/2) ))=((189)/(180)) (x^(1/2) /y^(1/2) )−1+(y^(1/2) /x^(1/2) )=((21)/(20)) (x^(1/2) /y^(1/2) )+(y^(1/2) /x^(1/2) )=((21)/(20))+1=((21+20)/(20))=((41)/(20)) t+(1/t)=((41)/(20)) [ t=(x^(1/2) /y^(1/2) )] 20t^2 −41t+20=0 t=(5/4),(4/5) (x^(1/2) /y^(1/2) )=(5/4),(4/5) (x/y)=((25)/(16)) , ((16)/(25)) x=((25)/(16))y , ((16)/(25))y putting these values in (i) x(√x) + y(√y) = 189 ⇒(((25)/(16))y)(√(((25)/(16))y))+y(√y)=189 ⇒(((16)/(25))y)(√(((16)/(25))y))+y(√y)=189 y(√y)(((125)/(64))+1)=189 y(√y)(((64)/(125))+1)=189 y(√y)(((189)/(64)))=189 y(√y)(((189)/(125)))=189 y^(3/2) =64 y^(3/2) =125 y=64^(2/3) =16 y=125^(2/3) =25 x=((25)/(16))y=((25)/(16))(16)=25 x=((16)/(25))y=((16)/(25))(25)=16 (x,y)=(16,25) or (25,16)](Q13928.png)
$$\mathrm{Answer}\:\mathrm{of}\:\mathrm{the}\:\mathrm{modified}\:\mathrm{question}. \\ $$$$\mathrm{Modification}\:\mathrm{suggested}\:\mathrm{by}\:\mathrm{ajfour}. \\ $$$$\mathrm{x}\sqrt{\mathrm{x}}\:+\:\mathrm{y}\sqrt{\mathrm{y}}\:=\:\mathrm{189}...........\left(\mathrm{i}\right) \\ $$$$\mathrm{x}\sqrt{\mathrm{y}}\:+\:\mathrm{y}\sqrt{\mathrm{x}}\:=\:\mathrm{180}............\left(\mathrm{ii}\right) \\ $$$$\left(\mathrm{i}\right)\Rightarrow\mathrm{x}^{\mathrm{3}/\mathrm{2}} +\mathrm{y}^{\mathrm{3}/\mathrm{2}} =\mathrm{189} \\ $$$$\:\Rightarrow\left(\mathrm{x}^{\mathrm{1}/\mathrm{2}} +\mathrm{y}^{\mathrm{1}/\mathrm{2}} \right)\left(\mathrm{x}−\mathrm{x}^{\mathrm{1}/\mathrm{2}} \mathrm{y}^{\mathrm{1}/\mathrm{2}} +\mathrm{y}\right)=\mathrm{189}....\left(\mathrm{iii}\right) \\ $$$$\left(\mathrm{ii}\right)\Rightarrow\mathrm{x}^{\mathrm{1}/\mathrm{2}} \mathrm{y}^{\mathrm{1}/\mathrm{2}} \left(\mathrm{x}^{\mathrm{1}/\mathrm{2}} +\mathrm{y}^{\mathrm{1}/\mathrm{2}} \right)=\mathrm{180}...\left(\mathrm{iv}\right) \\ $$$$\left(\mathrm{iii}\right)/\left(\mathrm{iv}\right):\frac{\mathrm{x}−\mathrm{x}^{\mathrm{1}/\mathrm{2}} \mathrm{y}^{\mathrm{1}/\mathrm{2}} +\mathrm{y}}{\mathrm{x}^{\mathrm{1}/\mathrm{2}} \mathrm{y}^{\mathrm{1}/\mathrm{2}} }=\frac{\mathrm{189}}{\mathrm{180}} \\ $$$$\frac{\mathrm{x}^{\mathrm{1}/\mathrm{2}} }{\mathrm{y}^{\mathrm{1}/\mathrm{2}} }−\mathrm{1}+\frac{\mathrm{y}^{\mathrm{1}/\mathrm{2}} }{\mathrm{x}^{\mathrm{1}/\mathrm{2}} }=\frac{\mathrm{21}}{\mathrm{20}} \\ $$$$\frac{\mathrm{x}^{\mathrm{1}/\mathrm{2}} }{\mathrm{y}^{\mathrm{1}/\mathrm{2}} }+\frac{\mathrm{y}^{\mathrm{1}/\mathrm{2}} }{\mathrm{x}^{\mathrm{1}/\mathrm{2}} }=\frac{\mathrm{21}}{\mathrm{20}}+\mathrm{1}=\frac{\mathrm{21}+\mathrm{20}}{\mathrm{20}}=\frac{\mathrm{41}}{\mathrm{20}} \\ $$$$\mathrm{t}+\frac{\mathrm{1}}{\mathrm{t}}=\frac{\mathrm{41}}{\mathrm{20}}\:\:\:\:\:\:\:\left[\:\mathrm{t}=\frac{\mathrm{x}^{\mathrm{1}/\mathrm{2}} }{\mathrm{y}^{\mathrm{1}/\mathrm{2}} }\right] \\ $$$$\mathrm{20t}^{\mathrm{2}} −\mathrm{41t}+\mathrm{20}=\mathrm{0} \\ $$$$\mathrm{t}=\frac{\mathrm{5}}{\mathrm{4}},\frac{\mathrm{4}}{\mathrm{5}} \\ $$$$\frac{\mathrm{x}^{\mathrm{1}/\mathrm{2}} }{\mathrm{y}^{\mathrm{1}/\mathrm{2}} }=\frac{\mathrm{5}}{\mathrm{4}},\frac{\mathrm{4}}{\mathrm{5}} \\ $$$$\frac{\mathrm{x}}{\mathrm{y}}=\frac{\mathrm{25}}{\mathrm{16}}\:\:,\:\:\frac{\mathrm{16}}{\mathrm{25}} \\ $$$$\mathrm{x}=\frac{\mathrm{25}}{\mathrm{16}}\mathrm{y}\:\:,\:\:\frac{\mathrm{16}}{\mathrm{25}}\mathrm{y} \\ $$$$\mathrm{putting}\:\mathrm{these}\:\mathrm{values}\:\mathrm{in}\:\left(\mathrm{i}\right) \\ $$$$\mathrm{x}\sqrt{\mathrm{x}}\:+\:\mathrm{y}\sqrt{\mathrm{y}}\:=\:\mathrm{189} \\ $$$$\Rightarrow\left(\frac{\mathrm{25}}{\mathrm{16}}\mathrm{y}\right)\sqrt{\frac{\mathrm{25}}{\mathrm{16}}\mathrm{y}}+\mathrm{y}\sqrt{\mathrm{y}}=\mathrm{189} \\ $$$$\Rightarrow\left(\frac{\mathrm{16}}{\mathrm{25}}\mathrm{y}\right)\sqrt{\frac{\mathrm{16}}{\mathrm{25}}\mathrm{y}}+\mathrm{y}\sqrt{\mathrm{y}}=\mathrm{189} \\ $$$$\:\:\:\:\mathrm{y}\sqrt{\mathrm{y}}\left(\frac{\mathrm{125}}{\mathrm{64}}+\mathrm{1}\right)=\mathrm{189} \\ $$$$\:\:\:\:\mathrm{y}\sqrt{\mathrm{y}}\left(\frac{\mathrm{64}}{\mathrm{125}}+\mathrm{1}\right)=\mathrm{189} \\ $$$$\:\:\:\:\mathrm{y}\sqrt{\mathrm{y}}\left(\frac{\mathrm{189}}{\mathrm{64}}\right)=\mathrm{189} \\ $$$$\:\:\:\:\mathrm{y}\sqrt{\mathrm{y}}\left(\frac{\mathrm{189}}{\mathrm{125}}\right)=\mathrm{189} \\ $$$$\mathrm{y}^{\mathrm{3}/\mathrm{2}} =\mathrm{64} \\ $$$$\mathrm{y}^{\mathrm{3}/\mathrm{2}} =\mathrm{125} \\ $$$$\mathrm{y}=\mathrm{64}^{\mathrm{2}/\mathrm{3}} =\mathrm{16} \\ $$$$\mathrm{y}=\mathrm{125}^{\mathrm{2}/\mathrm{3}} =\mathrm{25} \\ $$$$\mathrm{x}=\frac{\mathrm{25}}{\mathrm{16}}\mathrm{y}=\frac{\mathrm{25}}{\mathrm{16}}\left(\mathrm{16}\right)=\mathrm{25} \\ $$$$\mathrm{x}=\frac{\mathrm{16}}{\mathrm{25}}\mathrm{y}=\frac{\mathrm{16}}{\mathrm{25}}\left(\mathrm{25}\right)=\mathrm{16} \\ $$$$\left(\mathrm{x},\mathrm{y}\right)=\left(\mathrm{16},\mathrm{25}\right)\:\mathrm{or}\:\:\left(\mathrm{25},\mathrm{16}\right) \\ $$$$ \\ $$
Commented by tawa tawa last updated on 25/May/17

$$\mathrm{God}\:\mathrm{bless}\:\mathrm{you}\:\mathrm{sir} \\ $$
Answered by b.e.h.i.8.3.4.1.7@gmail.com last updated on 25/May/17
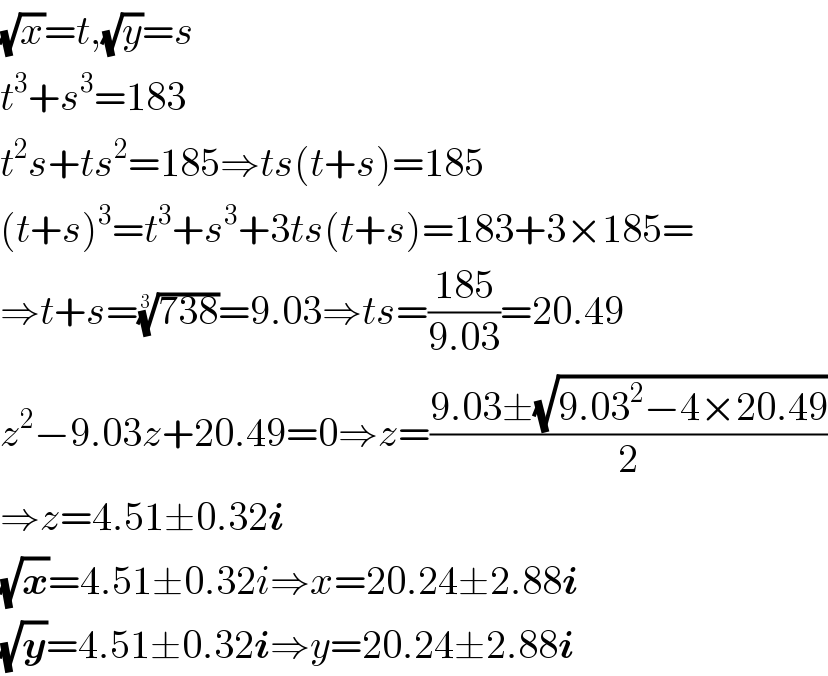
$$\sqrt{{x}}={t},\sqrt{{y}}={s} \\ $$$${t}^{\mathrm{3}} +{s}^{\mathrm{3}} =\mathrm{183} \\ $$$${t}^{\mathrm{2}} {s}+{ts}^{\mathrm{2}} =\mathrm{185}\Rightarrow{ts}\left({t}+{s}\right)=\mathrm{185} \\ $$$$\left({t}+{s}\right)^{\mathrm{3}} ={t}^{\mathrm{3}} +{s}^{\mathrm{3}} +\mathrm{3}{ts}\left({t}+{s}\right)=\mathrm{183}+\mathrm{3}×\mathrm{185}= \\ $$$$\Rightarrow{t}+{s}=\sqrt[{\mathrm{3}}]{\mathrm{738}}=\mathrm{9}.\mathrm{03}\Rightarrow{ts}=\frac{\mathrm{185}}{\mathrm{9}.\mathrm{03}}=\mathrm{20}.\mathrm{49} \\ $$$${z}^{\mathrm{2}} −\mathrm{9}.\mathrm{03}{z}+\mathrm{20}.\mathrm{49}=\mathrm{0}\Rightarrow{z}=\frac{\mathrm{9}.\mathrm{03}\pm\sqrt{\mathrm{9}.\mathrm{03}^{\mathrm{2}} −\mathrm{4}×\mathrm{20}.\mathrm{49}}}{\mathrm{2}} \\ $$$$\Rightarrow{z}=\mathrm{4}.\mathrm{51}\pm\mathrm{0}.\mathrm{32}\boldsymbol{{i}} \\ $$$$\sqrt{\boldsymbol{{x}}}=\mathrm{4}.\mathrm{51}\pm\mathrm{0}.\mathrm{32}{i}\Rightarrow{x}=\mathrm{20}.\mathrm{24}\pm\mathrm{2}.\mathrm{88}\boldsymbol{{i}} \\ $$$$\sqrt{\boldsymbol{{y}}}=\mathrm{4}.\mathrm{51}\pm\mathrm{0}.\mathrm{32}\boldsymbol{{i}}\Rightarrow{y}=\mathrm{20}.\mathrm{24}\pm\mathrm{2}.\mathrm{88}\boldsymbol{{i}} \\ $$
Commented by tawa tawa last updated on 25/May/17

$$\mathrm{God}\:\mathrm{bless}\:\mathrm{you}\:\mathrm{sir}. \\ $$
