
Question Number 5386 by sanusihammed last updated on 12/May/16

$${Solve}\:{simultaneously} \\ $$$$ \\ $$$${x}^{{x}} \:+\:\:{y}^{{y}\:} \:=\:\:\mathrm{31} \\ $$$${x}\:\:+\:\:{y}\:\:=\:\:\mathrm{5} \\ $$$$ \\ $$$${Please}\:{i}\:{did}\:{workings}\:... \\ $$$$ \\ $$$${Thanks}\:{for}\:{your}\:{help}. \\ $$
Commented by Rasheed Soomro last updated on 12/May/16

$$\mathrm{Trying}\:\mathrm{to}\:\mathrm{find}\:\mathrm{out}\:\mathrm{the}\:\mathrm{solution}\:\mathrm{in} \\ $$$$\mathrm{natural}\:\mathrm{numbers}: \\ $$$$\mathrm{Possible}\:\mathrm{solutions}\:\mathrm{for}\:\mathrm{x}+\mathrm{y}=\mathrm{5} \\ $$$$\mathrm{are}\:\left(\mathrm{1},\mathrm{4}\right),\left(\mathrm{2},\mathrm{3}\right),\left(\mathrm{3},\mathrm{2}\right),\left(\mathrm{4},\mathrm{1}\right) \\ $$$$\mathrm{Substituting}\:\mathrm{one}\:\mathrm{by}\:\mathrm{one}\:\mathrm{in}\:\mathrm{x}^{\mathrm{x}} +\mathrm{y}^{\mathrm{y}} =\mathrm{31} \\ $$$$\mathrm{we}\:\mathrm{will}\:\mathrm{find}\:\mathrm{that}\:\mathrm{only}\:\left(\mathrm{2},\mathrm{3}\right)\:\mathrm{and}\:\left(\mathrm{3},\mathrm{2}\right)\: \\ $$$$\mathrm{satisfy}\:\mathrm{the}\:\mathrm{equation}: \\ $$$$\mathrm{2}^{\mathrm{2}} +\mathrm{3}^{\mathrm{3}} =\mathrm{4}+\mathrm{27}=\mathrm{31}\:\mathrm{and} \\ $$$$\mathrm{3}^{\mathrm{3}} +\mathrm{2}^{\mathrm{2}} =\mathrm{27}+\mathrm{4}=\mathrm{31} \\ $$$$\mathrm{Hence}\:\left(\mathrm{2},\mathrm{3}\right)\:\mathrm{and}\:\left(\mathrm{3},\mathrm{2}\right)\:\mathrm{are}\:\mathrm{solutions}. \\ $$
Commented by sanusihammed last updated on 12/May/16
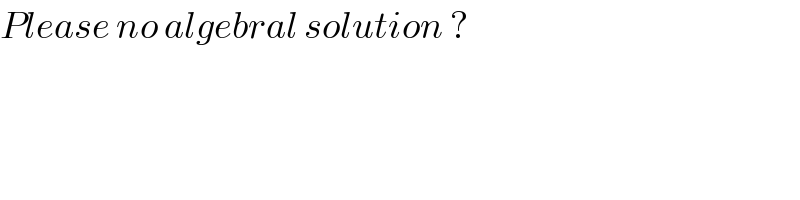
$${Please}\:{no}\:{algebral}\:{solution}\:? \\ $$
Commented by Rasheed Soomro last updated on 12/May/16
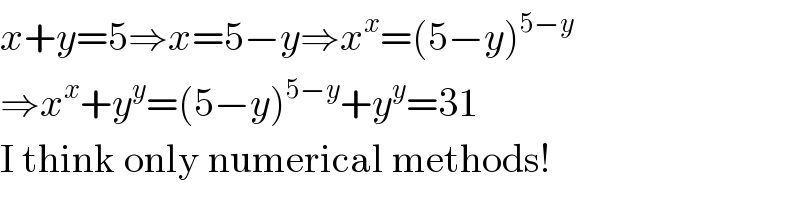
$${x}+{y}=\mathrm{5}\Rightarrow{x}=\mathrm{5}−{y}\Rightarrow{x}^{{x}} =\left(\mathrm{5}−{y}\right)^{\mathrm{5}−{y}} \\ $$$$\Rightarrow{x}^{{x}} +{y}^{{y}} =\left(\mathrm{5}−{y}\right)^{\mathrm{5}−{y}} +{y}^{{y}} =\mathrm{31} \\ $$$$\mathrm{I}\:\mathrm{think}\:\mathrm{only}\:\mathrm{numerical}\:\mathrm{methods}! \\ $$
