
Question Number 6824 by Tawakalitu. last updated on 30/Jul/16

$${Solve}\:{simultaneously} \\ $$$$\frac{\mathrm{1}}{{u}}\:+\:\frac{\mathrm{1}}{{v}}\:=\:\frac{\mathrm{1}}{\mathrm{3}}\:\:\:\:\:..........\:{equation}\:\left({i}\right) \\ $$$$\frac{{u}^{\mathrm{2}} }{{v}}\:+\:\frac{{v}^{\mathrm{2}} }{{u}}\:=\:\mathrm{12}\:\:\:\:\:\:........\:{equation}\:\left({ii}\right) \\ $$
Commented by sou1618 last updated on 30/Jul/16
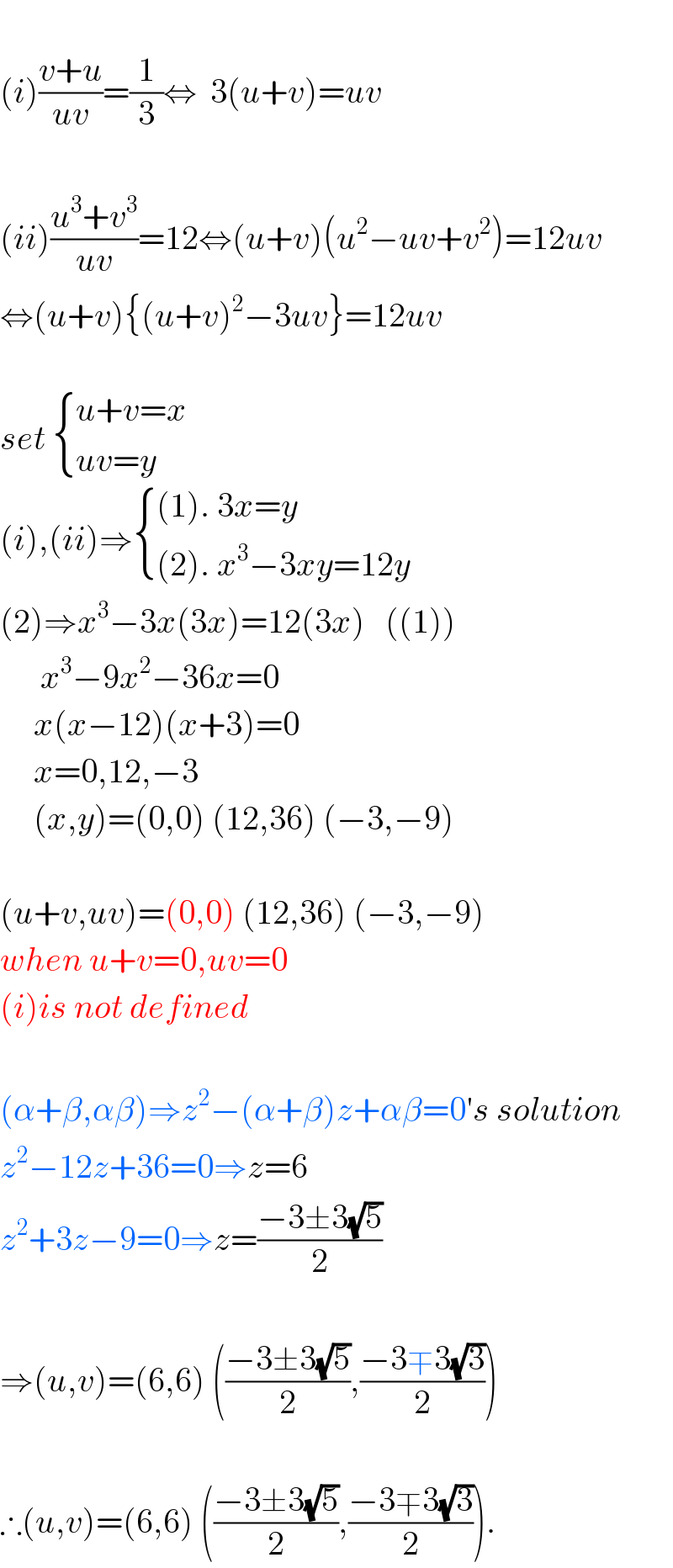
$$ \\ $$$$\left({i}\right)\frac{{v}+{u}}{{uv}}=\frac{\mathrm{1}}{\mathrm{3}}\Leftrightarrow\:\:\mathrm{3}\left({u}+{v}\right)={uv} \\ $$$$ \\ $$$$\left({ii}\right)\frac{{u}^{\mathrm{3}} +{v}^{\mathrm{3}} }{{uv}}=\mathrm{12}\Leftrightarrow\left({u}+{v}\right)\left({u}^{\mathrm{2}} −{uv}+{v}^{\mathrm{2}} \right)=\mathrm{12}{uv} \\ $$$$\Leftrightarrow\left({u}+{v}\right)\left\{\left({u}+{v}\right)^{\mathrm{2}} −\mathrm{3}{uv}\right\}=\mathrm{12}{uv} \\ $$$$ \\ $$$${set}\:\begin{cases}{{u}+{v}={x}}\\{{uv}={y}}\end{cases} \\ $$$$\left({i}\right),\left({ii}\right)\Rightarrow\begin{cases}{\left(\mathrm{1}\right).\:\mathrm{3}{x}={y}}\\{\left(\mathrm{2}\right).\:{x}^{\mathrm{3}} −\mathrm{3}{xy}=\mathrm{12}{y}}\end{cases} \\ $$$$\left(\mathrm{2}\right)\Rightarrow{x}^{\mathrm{3}} −\mathrm{3}{x}\left(\mathrm{3}{x}\right)=\mathrm{12}\left(\mathrm{3}{x}\right)\:\:\:\left(\left(\mathrm{1}\right)\right) \\ $$$$\:\:\:\:\:\:{x}^{\mathrm{3}} −\mathrm{9}{x}^{\mathrm{2}} −\mathrm{36}{x}=\mathrm{0} \\ $$$$\:\:\:\:\:{x}\left({x}−\mathrm{12}\right)\left({x}+\mathrm{3}\right)=\mathrm{0} \\ $$$$\:\:\:\:\:{x}=\mathrm{0},\mathrm{12},−\mathrm{3} \\ $$$$\:\:\:\:\:\left({x},{y}\right)=\left(\mathrm{0},\mathrm{0}\right)\:\left(\mathrm{12},\mathrm{36}\right)\:\left(−\mathrm{3},−\mathrm{9}\right) \\ $$$$ \\ $$$$\left({u}+{v},{uv}\right)=\left(\mathrm{0},\mathrm{0}\right)\:\left(\mathrm{12},\mathrm{36}\right)\:\left(−\mathrm{3},−\mathrm{9}\right) \\ $$$${when}\:{u}+{v}=\mathrm{0},{uv}=\mathrm{0} \\ $$$$\left({i}\right){is}\:{not}\:{defined} \\ $$$$ \\ $$$$\left(\alpha+\beta,\alpha\beta\right)\Rightarrow{z}^{\mathrm{2}} −\left(\alpha+\beta\right){z}+\alpha\beta=\mathrm{0}'{s}\:{solution} \\ $$$${z}^{\mathrm{2}} −\mathrm{12}{z}+\mathrm{36}=\mathrm{0}\Rightarrow{z}=\mathrm{6} \\ $$$${z}^{\mathrm{2}} +\mathrm{3}{z}−\mathrm{9}=\mathrm{0}\Rightarrow{z}=\frac{−\mathrm{3}\pm\mathrm{3}\sqrt{\mathrm{5}}}{\mathrm{2}} \\ $$$$ \\ $$$$\Rightarrow\left({u},{v}\right)=\left(\mathrm{6},\mathrm{6}\right)\:\left(\frac{−\mathrm{3}\pm\mathrm{3}\sqrt{\mathrm{5}}}{\mathrm{2}},\frac{−\mathrm{3}\mp\mathrm{3}\sqrt{\mathrm{3}}}{\mathrm{2}}\right) \\ $$$$ \\ $$$$\therefore\left({u},{v}\right)=\left(\mathrm{6},\mathrm{6}\right)\:\left(\frac{−\mathrm{3}\pm\mathrm{3}\sqrt{\mathrm{5}}}{\mathrm{2}},\frac{−\mathrm{3}\mp\mathrm{3}\sqrt{\mathrm{3}}}{\mathrm{2}}\right). \\ $$
Commented by Tawakalitu. last updated on 30/Jul/16
$${Thanks}\:{for}\:{your}\:{help}.\:{i}\:{appreciate}. \\ $$
