
Question Number 198132 by a.lgnaoui last updated on 11/Oct/23
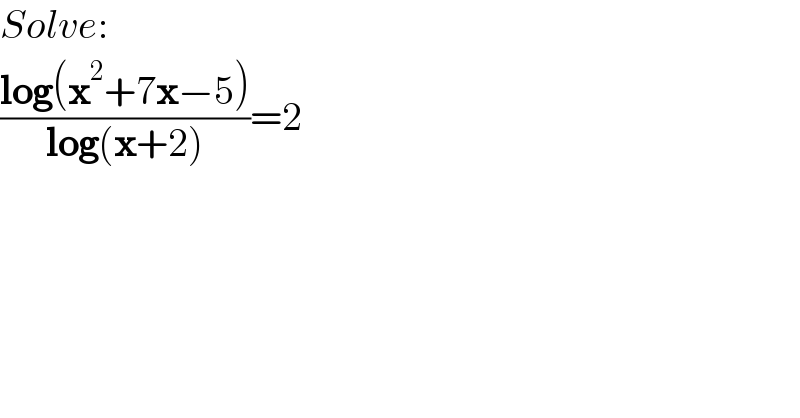
$${Solve}: \\ $$$$\frac{\boldsymbol{\mathrm{log}}\left(\boldsymbol{\mathrm{x}}^{\mathrm{2}} +\mathrm{7}\boldsymbol{\mathrm{x}}−\mathrm{5}\right)}{\boldsymbol{\mathrm{log}}\left(\boldsymbol{\mathrm{x}}+\mathrm{2}\right)}=\mathrm{2} \\ $$
Answered by som(math1967) last updated on 11/Oct/23
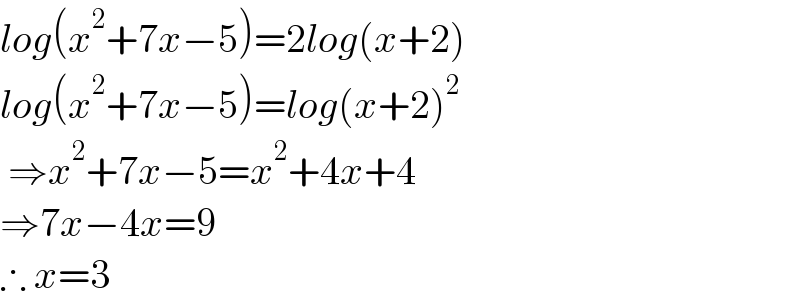
$${log}\left({x}^{\mathrm{2}} +\mathrm{7}{x}−\mathrm{5}\right)=\mathrm{2}{log}\left({x}+\mathrm{2}\right) \\ $$$${log}\left({x}^{\mathrm{2}} +\mathrm{7}{x}−\mathrm{5}\right)={log}\left({x}+\mathrm{2}\right)^{\mathrm{2}} \\ $$$$\:\Rightarrow{x}^{\mathrm{2}} +\mathrm{7}{x}−\mathrm{5}={x}^{\mathrm{2}} +\mathrm{4}{x}+\mathrm{4} \\ $$$$\Rightarrow\mathrm{7}{x}−\mathrm{4}{x}=\mathrm{9} \\ $$$$\therefore\:{x}=\mathrm{3} \\ $$
Commented by a.lgnaoui last updated on 11/Oct/23

$$\mathrm{exact} \\ $$
