
Question Number 121899 by ZiYangLee last updated on 12/Nov/20
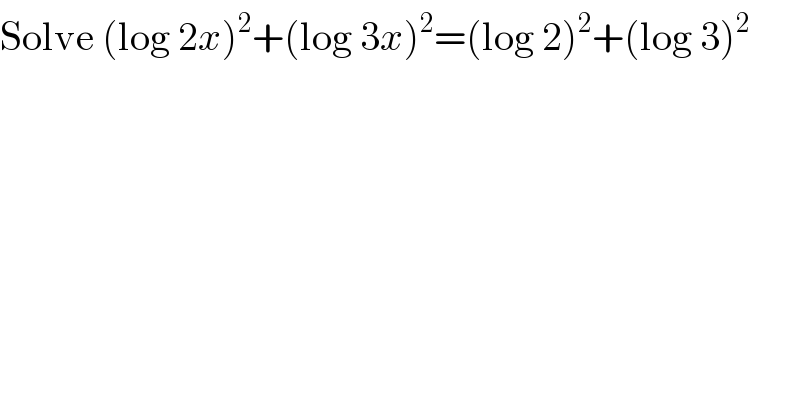
$$\mathrm{Solve}\:\left(\mathrm{log}\:\mathrm{2}{x}\right)^{\mathrm{2}} +\left(\mathrm{log}\:\mathrm{3}{x}\right)^{\mathrm{2}} =\left(\mathrm{log}\:\mathrm{2}\right)^{\mathrm{2}} +\left(\mathrm{log}\:\mathrm{3}\right)^{\mathrm{2}} \\ $$
Commented by Dwaipayan Shikari last updated on 12/Nov/20
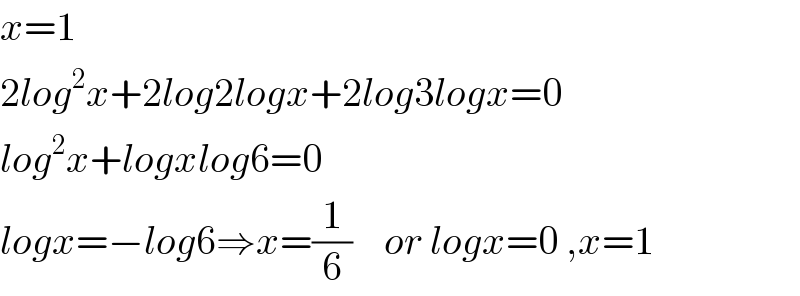
$${x}=\mathrm{1} \\ $$$$\mathrm{2}{log}^{\mathrm{2}} {x}+\mathrm{2}{log}\mathrm{2}{logx}+\mathrm{2}{log}\mathrm{3}{logx}=\mathrm{0} \\ $$$${log}^{\mathrm{2}} {x}+{logxlog}\mathrm{6}=\mathrm{0} \\ $$$${logx}=−{log}\mathrm{6}\Rightarrow{x}=\frac{\mathrm{1}}{\mathrm{6}}\:\:\:\:{or}\:{logx}=\mathrm{0}\:,{x}=\mathrm{1} \\ $$
Commented by ZiYangLee last updated on 12/Nov/20

$$\mathrm{thanks}\:\mathrm{sir} \\ $$
Answered by MJS_new last updated on 12/Nov/20
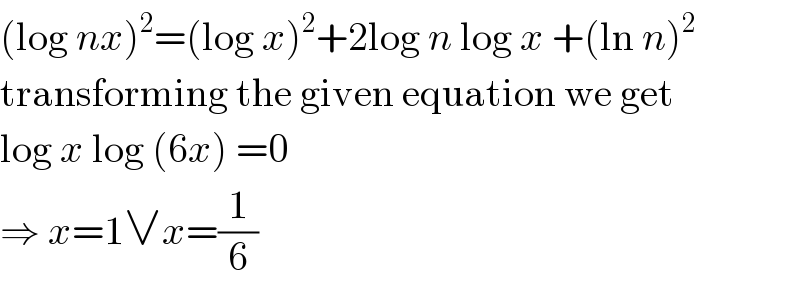
$$\left(\mathrm{log}\:{nx}\right)^{\mathrm{2}} =\left(\mathrm{log}\:{x}\right)^{\mathrm{2}} +\mathrm{2log}\:{n}\:\mathrm{log}\:{x}\:+\left(\mathrm{ln}\:{n}\right)^{\mathrm{2}} \\ $$$$\mathrm{transforming}\:\mathrm{the}\:\mathrm{given}\:\mathrm{equation}\:\mathrm{we}\:\mathrm{get} \\ $$$$\mathrm{log}\:{x}\:\mathrm{log}\:\left(\mathrm{6}{x}\right)\:=\mathrm{0} \\ $$$$\Rightarrow\:{x}=\mathrm{1}\vee{x}=\frac{\mathrm{1}}{\mathrm{6}} \\ $$
Commented by ZiYangLee last updated on 12/Nov/20

$$\mathrm{Thanks}\:\mathrm{sir}..\bigstar \\ $$
