
Question Number 205114 by 2kdw last updated on 09/Mar/24
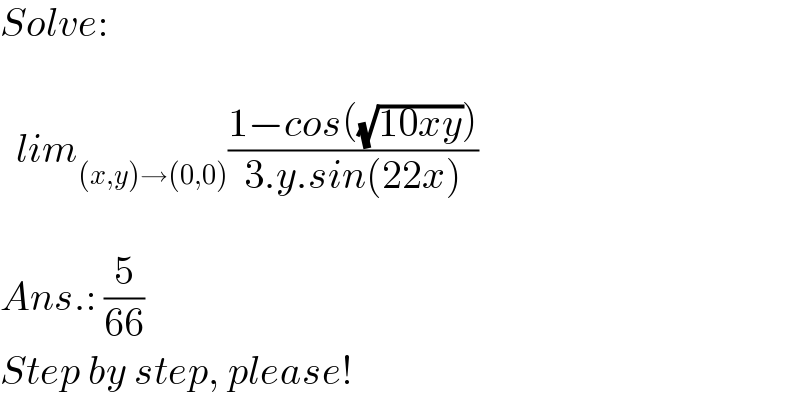
$${Solve}: \\ $$$$ \\ $$$$\:\:{lim}_{\left({x},{y}\right)\rightarrow\left(\mathrm{0},\mathrm{0}\right)} \frac{\mathrm{1}−{cos}\left(\sqrt{\mathrm{10}{xy}}\right)}{\mathrm{3}.{y}.{sin}\left(\mathrm{22}{x}\right)} \\ $$$$ \\ $$$${Ans}.:\:\frac{\mathrm{5}}{\mathrm{66}} \\ $$$${Step}\:{by}\:{step},\:{please}! \\ $$
Answered by MM42 last updated on 09/Mar/24
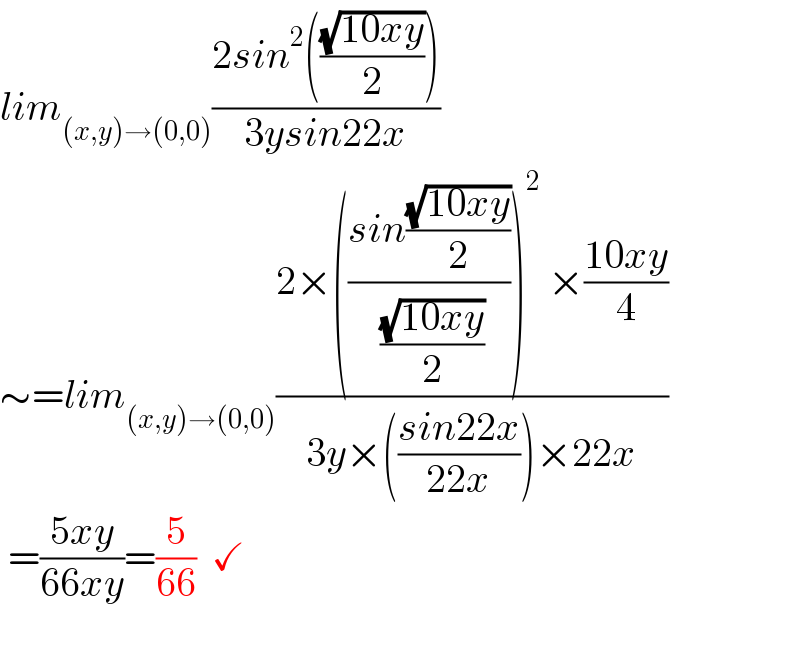
$${lim}_{\left({x},{y}\right)\rightarrow\left(\mathrm{0},\mathrm{0}\right)} \frac{\mathrm{2}{sin}^{\mathrm{2}} \left(\frac{\sqrt{\mathrm{10}{xy}}}{\mathrm{2}}\right)}{\mathrm{3}{ysin}\mathrm{22}{x}} \\ $$$$\sim={lim}_{\left({x},{y}\right)\rightarrow\left(\mathrm{0},\mathrm{0}\right)} \frac{\mathrm{2}×\left(\frac{{sin}\frac{\sqrt{\mathrm{10}{xy}}}{\mathrm{2}}}{\:\frac{\sqrt{\mathrm{10}{xy}}}{\mathrm{2}}}\right)^{\mathrm{2}} \:×\frac{\mathrm{10}{xy}}{\mathrm{4}}}{\mathrm{3}{y}×\left(\frac{{sin}\mathrm{22}{x}}{\mathrm{22}{x}}\right)×\mathrm{22}{x}}\: \\ $$$$\:=\frac{\mathrm{5}{xy}}{\mathrm{66}{xy}}=\frac{\mathrm{5}}{\mathrm{66}}\:\:\checkmark \\ $$$$ \\ $$
Commented by 2kdw last updated on 09/Mar/24
Thanks Sir
Commented by lepuissantcedricjunior last updated on 12/Mar/24

$$\boldsymbol{{good}}\:!!! \\ $$
