Question and Answers Forum

All Questions      Topic List

Algebra Questions

Previous in All Question      Next in All Question      

Previous in Algebra      Next in Algebra      

Question Number 47993 by F_Nongue last updated on 18/Nov/18

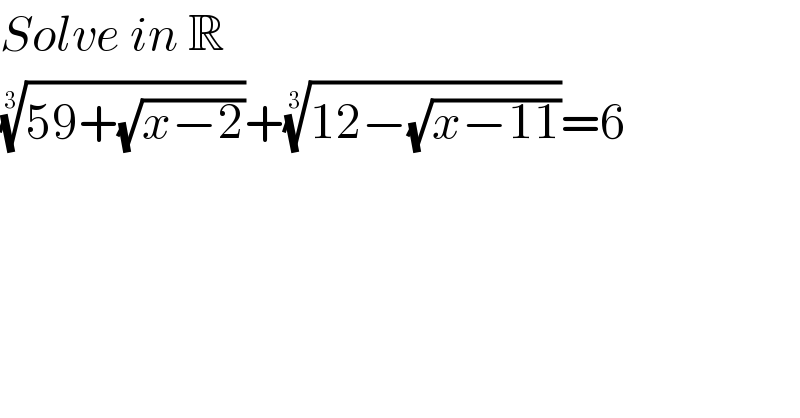
Solve in R ((59+(√(x−2))))^(1/3) +((12−(√(x−11))))^(1/3) =6

$${Solve}\:{in}\:\mathbb{R} \\ $$$$\sqrt[{\mathrm{3}}]{\mathrm{59}+\sqrt{{x}−\mathrm{2}}}+\sqrt[{\mathrm{3}}]{\mathrm{12}−\sqrt{{x}−\mathrm{11}}}=\mathrm{6} \\ $$

Commented by tanmay.chaudhury50@gmail.com last updated on 18/Nov/18

x=27

$${x}=\mathrm{27} \\ $$

Commented by ajfour last updated on 18/Nov/18

steps please..

$${steps}\:{please}.. \\ $$

Commented by MJS last updated on 18/Nov/18

we can try or we can eliminate all roots which leads to a polynome of 5^(th) degree ⇒ we can only try again. is there an easier way? [putting x=t+((13)/2) helps while transforming]

$$\mathrm{we}\:\mathrm{can}\:\mathrm{try} \\ $$$$\mathrm{or} \\ $$$$\mathrm{we}\:\mathrm{can}\:\mathrm{eliminate}\:\mathrm{all}\:\mathrm{roots}\:\mathrm{which}\:\mathrm{leads}\:\mathrm{to} \\ $$$$\mathrm{a}\:\mathrm{polynome}\:\mathrm{of}\:\mathrm{5}^{\mathrm{th}} \:\mathrm{degree}\:\Rightarrow\:\mathrm{we}\:\mathrm{can}\:\mathrm{only}\:\mathrm{try} \\ $$$$\mathrm{again}.\:\mathrm{is}\:\mathrm{there}\:\mathrm{an}\:\mathrm{easier}\:\mathrm{way}? \\ $$$$\left[\mathrm{putting}\:{x}={t}+\frac{\mathrm{13}}{\mathrm{2}}\:\mathrm{helps}\:\mathrm{while}\:\mathrm{transforming}\right] \\ $$

Commented by MJS last updated on 18/Nov/18

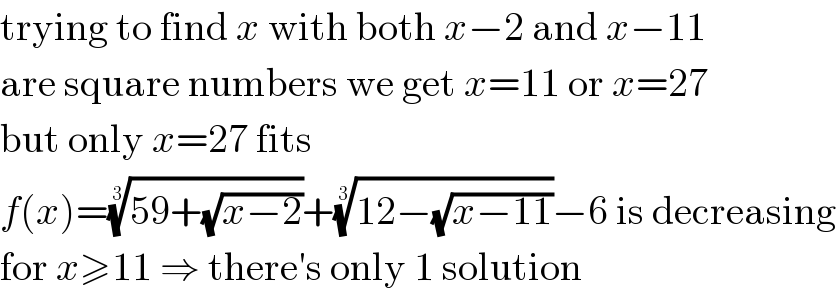
trying to find x with both x−2 and x−11 are square numbers we get x=11 or x=27 but only x=27 fits f(x)=((59+(√(x−2))))^(1/3) +((12−(√(x−11))))^(1/3) −6 is decreasing for x≥11 ⇒ there′s only 1 solution

$$\mathrm{trying}\:\mathrm{to}\:\mathrm{find}\:{x}\:\mathrm{with}\:\mathrm{both}\:{x}−\mathrm{2}\:\mathrm{and}\:{x}−\mathrm{11} \\ $$$$\mathrm{are}\:\mathrm{square}\:\mathrm{numbers}\:\mathrm{we}\:\mathrm{get}\:{x}=\mathrm{11}\:\mathrm{or}\:{x}=\mathrm{27} \\ $$$$\mathrm{but}\:\mathrm{only}\:{x}=\mathrm{27}\:\mathrm{fits} \\ $$$${f}\left({x}\right)=\sqrt[{\mathrm{3}}]{\mathrm{59}+\sqrt{{x}−\mathrm{2}}}+\sqrt[{\mathrm{3}}]{\mathrm{12}−\sqrt{{x}−\mathrm{11}}}−\mathrm{6}\:\mathrm{is}\:\mathrm{decreasing} \\ $$$$\mathrm{for}\:{x}\geqslant\mathrm{11}\:\Rightarrow\:\mathrm{there}'\mathrm{s}\:\mathrm{only}\:\mathrm{1}\:\mathrm{solution} \\ $$

Commented by tanmay.chaudhury50@gmail.com last updated on 18/Nov/18

from problem... 1)x>2 and x>11 i have solved logically 6=1+5 6=2+4 6=3+3 that means 59+(√(x−2)) =64 x−2=25 x=27 12−(√(x−11)) =8 (√(x−11)) =4 x=27

$${from}\:{problem}... \\ $$$$\left.\:\:\mathrm{1}\right){x}>\mathrm{2}\:{and}\:{x}>\mathrm{11} \\ $$$${i}\:{have}\:{solved}\:{logically} \\ $$$$\mathrm{6}=\mathrm{1}+\mathrm{5} \\ $$$$\mathrm{6}=\mathrm{2}+\mathrm{4} \\ $$$$\mathrm{6}=\mathrm{3}+\mathrm{3} \\ $$$${that}\:{means} \\ $$$$\mathrm{59}+\sqrt{{x}−\mathrm{2}}\:=\mathrm{64} \\ $$$${x}−\mathrm{2}=\mathrm{25}\:\:\:{x}=\mathrm{27} \\ $$$$\mathrm{12}−\sqrt{{x}−\mathrm{11}}\:=\mathrm{8} \\ $$$$\sqrt{{x}−\mathrm{11}}\:=\mathrm{4} \\ $$$${x}=\mathrm{27} \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com