
Question Number 156361 by mr W last updated on 10/Oct/21
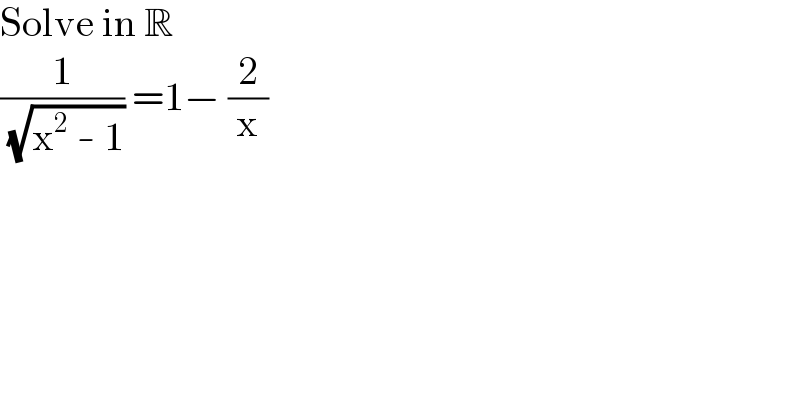
$$\mathrm{Solve}\:\mathrm{in}\:\mathbb{R} \\ $$$$\frac{\mathrm{1}}{\:\sqrt{\mathrm{x}^{\mathrm{2}} \:-\:\mathrm{1}}}\:=\mathrm{1}−\:\frac{\mathrm{2}}{\mathrm{x}} \\ $$
Commented by cortano last updated on 11/Oct/21
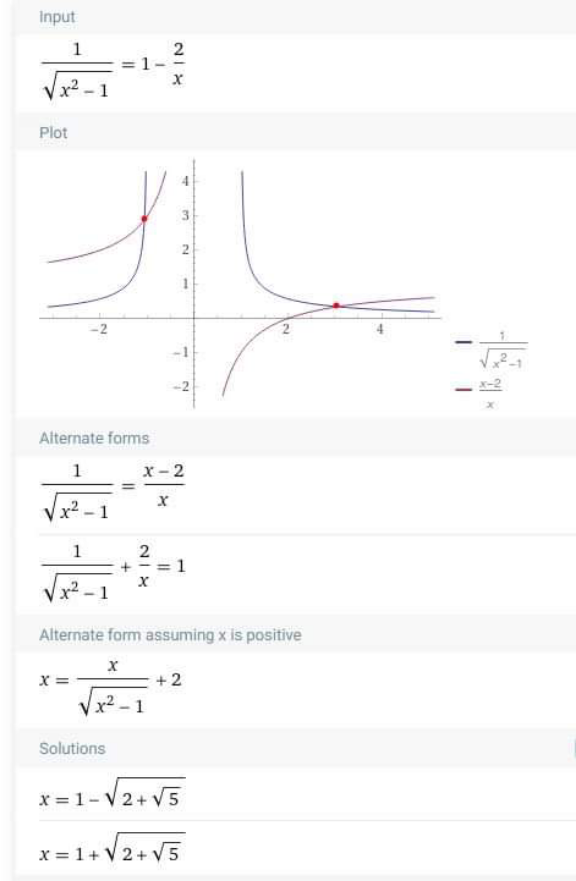
Commented by mr W last updated on 11/Oct/21
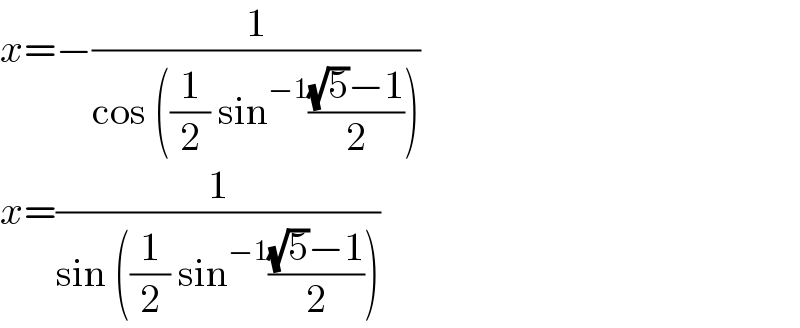
$${x}=−\frac{\mathrm{1}}{\mathrm{cos}\:\left(\frac{\mathrm{1}}{\mathrm{2}}\:\mathrm{sin}^{−\mathrm{1}} \frac{\sqrt{\mathrm{5}}−\mathrm{1}}{\mathrm{2}}\right)}\: \\ $$$${x}=\frac{\mathrm{1}}{\mathrm{sin}\:\left(\frac{\mathrm{1}}{\mathrm{2}}\:\mathrm{sin}^{−\mathrm{1}} \frac{\sqrt{\mathrm{5}}−\mathrm{1}}{\mathrm{2}}\right)} \\ $$
Answered by MJS_new last updated on 10/Oct/21
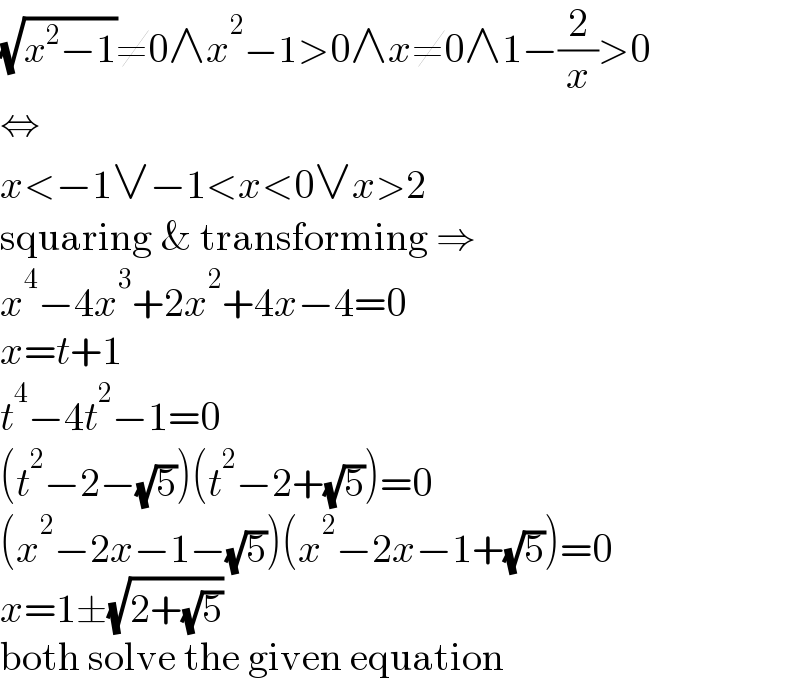
$$\sqrt{{x}^{\mathrm{2}} −\mathrm{1}}\neq\mathrm{0}\wedge{x}^{\mathrm{2}} −\mathrm{1}>\mathrm{0}\wedge{x}\neq\mathrm{0}\wedge\mathrm{1}−\frac{\mathrm{2}}{{x}}>\mathrm{0} \\ $$$$\Leftrightarrow \\ $$$${x}<−\mathrm{1}\vee−\mathrm{1}<{x}<\mathrm{0}\vee{x}>\mathrm{2} \\ $$$$\mathrm{squaring}\:\&\:\mathrm{transforming}\:\Rightarrow \\ $$$${x}^{\mathrm{4}} −\mathrm{4}{x}^{\mathrm{3}} +\mathrm{2}{x}^{\mathrm{2}} +\mathrm{4}{x}−\mathrm{4}=\mathrm{0} \\ $$$${x}={t}+\mathrm{1} \\ $$$${t}^{\mathrm{4}} −\mathrm{4}{t}^{\mathrm{2}} −\mathrm{1}=\mathrm{0} \\ $$$$\left({t}^{\mathrm{2}} −\mathrm{2}−\sqrt{\mathrm{5}}\right)\left({t}^{\mathrm{2}} −\mathrm{2}+\sqrt{\mathrm{5}}\right)=\mathrm{0} \\ $$$$\left({x}^{\mathrm{2}} −\mathrm{2}{x}−\mathrm{1}−\sqrt{\mathrm{5}}\right)\left({x}^{\mathrm{2}} −\mathrm{2}{x}−\mathrm{1}+\sqrt{\mathrm{5}}\right)=\mathrm{0} \\ $$$${x}=\mathrm{1}\pm\sqrt{\mathrm{2}+\sqrt{\mathrm{5}}} \\ $$$$\mathrm{both}\:\mathrm{solve}\:\mathrm{the}\:\mathrm{given}\:\mathrm{equation} \\ $$
Commented by mr W last updated on 10/Oct/21

$${thanks}\:{sir}! \\ $$
Commented by MJS_new last updated on 10/Oct/21
$$\mathrm{it}\:\mathrm{was}\:\mathrm{just}\:\mathrm{a}\:\mathrm{typo}\:\mathrm{in}\:\mathrm{the}\:\mathrm{first}\:\mathrm{line}\:\mathrm{which}\:\mathrm{I} \\ $$$$\mathrm{inserted}\:\mathrm{later} \\ $$
