
Question Number 172210 by Rasheed.Sindhi last updated on 24/Jun/22

$$\boldsymbol{\mathrm{Solve}}\:\boldsymbol{\mathrm{in}}\:\mathbb{N}: \\ $$$$\mathrm{6}^{\boldsymbol{\mathrm{x}}} +\mathrm{6}^{\boldsymbol{\mathrm{y}}} =\mathrm{222} \\ $$
Commented by infinityaction last updated on 24/Jun/22

$$\left(\mathrm{1},\mathrm{3}\right)\:{and}\:\left(\mathrm{3},\mathrm{1}\right) \\ $$
Commented by Rasheed.Sindhi last updated on 24/Jun/22
$$\mathrm{Correct}\:\mathrm{sir}!\:\mathrm{Process}\:\mathrm{please}! \\ $$
Commented by infinityaction last updated on 22/Jul/22
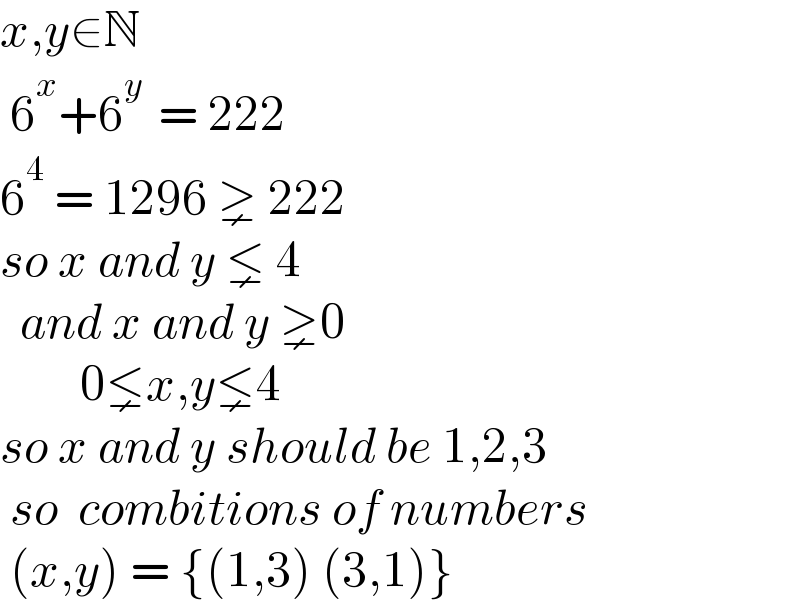
$${x},{y}\in\mathbb{N} \\ $$$$\:\mathrm{6}^{{x}} +\mathrm{6}^{{y}\:} \:=\:\mathrm{222} \\ $$$$\mathrm{6}^{\mathrm{4}} \:=\:\mathrm{1296}\:\gneq\:\mathrm{222} \\ $$$${so}\:{x}\:{and}\:{y}\:\lneq\:\mathrm{4} \\ $$$$\:\:{and}\:{x}\:{and}\:{y}\:\gneq\mathrm{0} \\ $$$$\:\:\:\:\:\:\:\:\mathrm{0}\lneq{x},{y}\lneq\mathrm{4} \\ $$$${so}\:{x}\:{and}\:{y}\:{should}\:{be}\:\mathrm{1},\mathrm{2},\mathrm{3} \\ $$$$\:{so}\:\:{combitions}\:{of}\:{numbers} \\ $$$$\:\left({x},{y}\right)\:=\:\left\{\left(\mathrm{1},\mathrm{3}\right)\:\left(\mathrm{3},\mathrm{1}\right)\right\} \\ $$
Commented by Rasheed.Sindhi last updated on 24/Jun/22

$$\mathcal{T}{han}\mathcal{X}\:{sir}! \\ $$
Answered by Rasheed.Sindhi last updated on 24/Jun/22
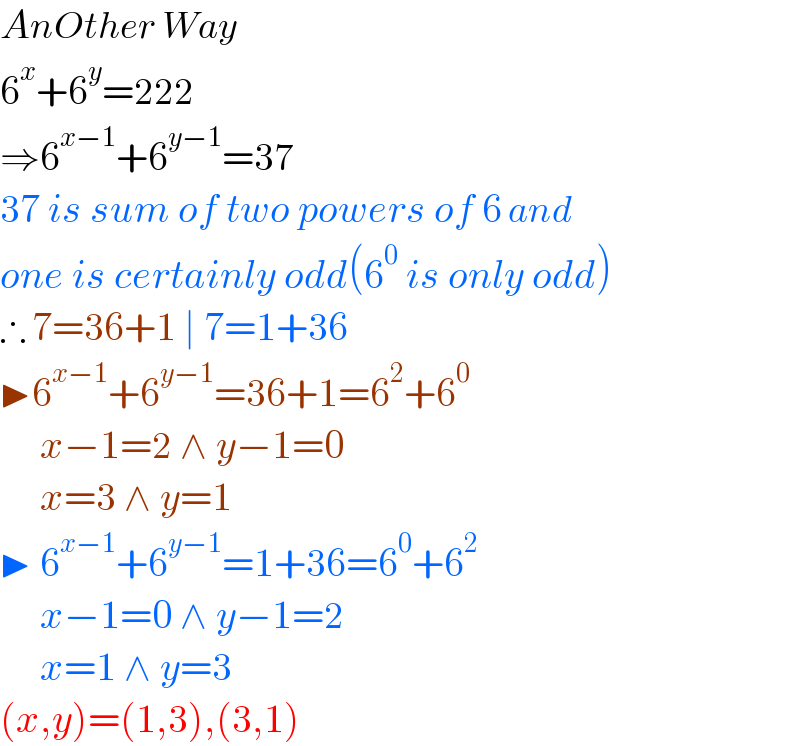
$${AnOther}\:{Way} \\ $$$$\mathrm{6}^{{x}} +\mathrm{6}^{{y}} =\mathrm{222} \\ $$$$\Rightarrow\mathrm{6}^{{x}−\mathrm{1}} +\mathrm{6}^{{y}−\mathrm{1}} =\mathrm{37} \\ $$$$\mathrm{37}\:{is}\:{sum}\:{of}\:{two}\:{powers}\:{of}\:\mathrm{6}\:{and} \\ $$$${one}\:{is}\:{certainly}\:{odd}\left(\mathrm{6}^{\mathrm{0}} \:{is}\:{only}\:{odd}\right) \\ $$$$\therefore\:\mathrm{7}=\mathrm{36}+\mathrm{1}\:\mid\:\mathrm{7}=\mathrm{1}+\mathrm{36} \\ $$$$\blacktriangleright\mathrm{6}^{{x}−\mathrm{1}} +\mathrm{6}^{{y}−\mathrm{1}} =\mathrm{36}+\mathrm{1}=\mathrm{6}^{\mathrm{2}} +\mathrm{6}^{\mathrm{0}} \\ $$$$\:\:\:\:\:{x}−\mathrm{1}=\mathrm{2}\:\wedge\:{y}−\mathrm{1}=\mathrm{0} \\ $$$$\:\:\:\:\:{x}=\mathrm{3}\:\wedge\:{y}=\mathrm{1} \\ $$$$\blacktriangleright\:\mathrm{6}^{{x}−\mathrm{1}} +\mathrm{6}^{{y}−\mathrm{1}} =\mathrm{1}+\mathrm{36}=\mathrm{6}^{\mathrm{0}} +\mathrm{6}^{\mathrm{2}} \\ $$$$\:\:\:\:\:{x}−\mathrm{1}=\mathrm{0}\:\wedge\:{y}−\mathrm{1}=\mathrm{2} \\ $$$$\:\:\:\:\:{x}=\mathrm{1}\:\wedge\:{y}=\mathrm{3} \\ $$$$\left({x},{y}\right)=\left(\mathrm{1},\mathrm{3}\right),\left(\mathrm{3},\mathrm{1}\right) \\ $$
Commented by infinityaction last updated on 24/Jun/22

$${nice}\:{sir} \\ $$
Commented by Rasheed.Sindhi last updated on 24/Jun/22

🙏🙏🙏
Answered by kapoorshah last updated on 24/Jun/22
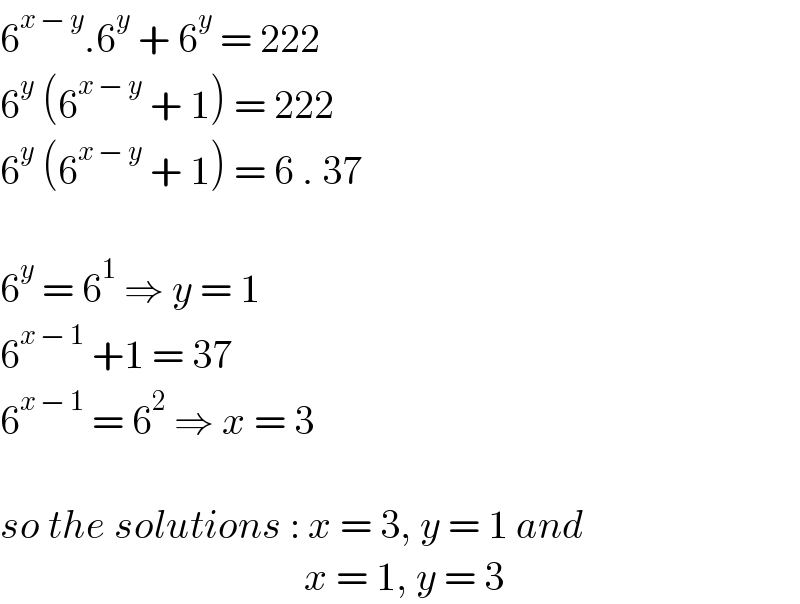
$$\mathrm{6}^{{x}\:−\:{y}} .\mathrm{6}^{{y}} \:+\:\mathrm{6}^{{y}} \:=\:\mathrm{222} \\ $$$$\mathrm{6}^{{y}} \:\left(\mathrm{6}^{{x}\:−\:{y}} \:+\:\mathrm{1}\right)\:=\:\mathrm{222} \\ $$$$\mathrm{6}^{{y}} \:\left(\mathrm{6}^{{x}\:−\:{y}} \:+\:\mathrm{1}\right)\:=\:\mathrm{6}\:.\:\mathrm{37} \\ $$$$ \\ $$$$\mathrm{6}^{{y}} \:=\:\mathrm{6}^{\mathrm{1}} \:\Rightarrow\:{y}\:=\:\mathrm{1} \\ $$$$\mathrm{6}^{{x}\:−\:\mathrm{1}} \:+\mathrm{1}\:=\:\mathrm{37} \\ $$$$\mathrm{6}^{{x}\:−\:\mathrm{1}} \:=\:\mathrm{6}^{\mathrm{2}} \:\Rightarrow\:{x}\:=\:\mathrm{3} \\ $$$$ \\ $$$${so}\:{the}\:{solutions}\::\:{x}\:=\:\mathrm{3},\:{y}\:=\:\mathrm{1}\:{and}\: \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:{x}\:=\:\mathrm{1},\:{y}\:=\:\mathrm{3} \\ $$
Commented by Rasheed.Sindhi last updated on 24/Jun/22

$$\mathbb{T}\boldsymbol{\mathrm{han}}\Bbbk\boldsymbol{\mathrm{s}}\:\mathrm{sir}! \\ $$
