
Question Number 23687 by tawa tawa last updated on 03/Nov/17
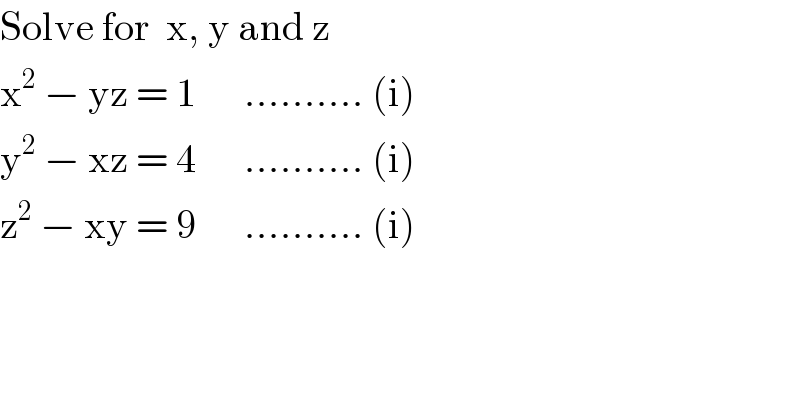
$$\mathrm{Solve}\:\mathrm{for}\:\:\mathrm{x},\:\mathrm{y}\:\mathrm{and}\:\mathrm{z} \\ $$$$\mathrm{x}^{\mathrm{2}} \:−\:\mathrm{yz}\:=\:\mathrm{1}\:\:\:\:\:\:..........\:\left(\mathrm{i}\right) \\ $$$$\mathrm{y}^{\mathrm{2}} \:−\:\mathrm{xz}\:=\:\mathrm{4}\:\:\:\:\:\:..........\:\left(\mathrm{i}\right) \\ $$$$\mathrm{z}^{\mathrm{2}} \:−\:\mathrm{xy}\:=\:\mathrm{9}\:\:\:\:\:\:..........\:\left(\mathrm{i}\right) \\ $$
Answered by ajfour last updated on 04/Nov/17
![If we add the three eqns. x^2 +y^2 +z^2 −xy−yz−zx=14 or (x−y)^2 +(y−z)^2 +(z−x)^2 =28 .....(i) ...from given equations: (y−x)(x+y+z)=3 .....(a) (z−y)(x+y+z)=5 ......(b) (x−z)(x+y+z)=−8 .....(c) hence y−z=(5/3)(x−y) ....(d) z−x=((−8)/3)(x−y) .....(e) replacing in (i) we get, (x−y)^2 [1+((25)/9)+((64)/9)]=28 or (x−y)^2 =((18)/7) .....(f) squaring and adding eqns. (a),(b), and (c) we get (x+y+z)^2 ×28 =9+25+64 =98 or (x+y+z)^2 =(7/2) .....(g) From (d) and (e): (y−z)=(5/3)(x−y) and (z−x)=((−8)/3)(x−y) we get 5x−8y +3z =0 ...(h) From (g) , If x+y+z =+((√7)/(√2)) using this in (a), y−x = ((3(√2))/(√7)) , and using it in(b) z−y = ((5(√2))/(√7)) , and in (c) to get x−z = ((−8(√2))/(√7)) . x+y+z = ((√7)/(√2)) ⇒ x+(x+((3(√2))/(√7)))+(x+((8(√2))/(√7)))=((√7)/(√2)) ⇒ 3x =((√7)/(√2))−((11(√2))/(√7)) = −((15)/(√(14))) or x =− (5/(√(14))) y = x+((3(√2))/(√7)) = −(5/(√(14)))+(6/(√(14))) or y= (1/(√(14))) and z =x+((8(√2))/(√7)) = ((−5)/(√(14)))+((16)/(√(14))) or z = ((11)/(√(14))) . So one solution is (((−5)/(√(14))) , (1/(√(14))) , ((11)/(√(14)))) (Answer). and to get the other one we shall take x+y+z = −((√7)/(√2)) ⇒ 3x−((3(√2))/(√7))−((8(√2))/(√7)) =((−(√7))/(√2)) ⇒ x= (1/3)(((22)/(√(14)))−(7/(√(14)))) = (5/(3(√(14)))) y=x−((3(√2))/(√7)) = ((−13)/(3(√(14)))) and z = x−((8(√2))/(√7)) = ((−43)/(3(√(14)))) so other solution is ((5/(3(√(14)))) , ((−13)/(3(√(14)))) , ((−43)/(3(√(14)))) ) . this one dont seem to agree...?!](Q23705.png)
$$ \\ $$$$\:{If}\:{we}\:{add}\:{the}\:{three}\:{eqns}. \\ $$$${x}^{\mathrm{2}} +{y}^{\mathrm{2}} +{z}^{\mathrm{2}} \:−{xy}−{yz}−{zx}=\mathrm{14} \\ $$$${or}\:\:\left({x}−{y}\right)^{\mathrm{2}} +\left({y}−{z}\right)^{\mathrm{2}} +\left({z}−{x}\right)^{\mathrm{2}} \:=\mathrm{28} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:.....\left({i}\right) \\ $$$$...{from}\:{given}\:{equations}: \\ $$$$\:\:\left({y}−{x}\right)\left({x}+{y}+{z}\right)=\mathrm{3}\:\:\:\:\:\:\:\:.....\left({a}\right) \\ $$$$\:\:\left({z}−{y}\right)\left({x}+{y}+{z}\right)=\mathrm{5}\:\:\:\:\:\:\:\:......\left({b}\right) \\ $$$$\:\:\:\left({x}−{z}\right)\left({x}+{y}+{z}\right)=−\mathrm{8}\:\:\:\:\:\:.....\left({c}\right) \\ $$$${hence}\:\:\:{y}−{z}=\frac{\mathrm{5}}{\mathrm{3}}\left({x}−{y}\right)\:\:\:\:\:\:....\left({d}\right) \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:{z}−{x}=\frac{−\mathrm{8}}{\mathrm{3}}\left({x}−{y}\right)\:\:\:\:\:\:.....\left({e}\right) \\ $$$${replacing}\:{in}\:\left({i}\right)\:{we}\:{get}, \\ $$$$\left({x}−{y}\right)^{\mathrm{2}} \left[\mathrm{1}+\frac{\mathrm{25}}{\mathrm{9}}+\frac{\mathrm{64}}{\mathrm{9}}\right]=\mathrm{28} \\ $$$${or}\:\:\:\:\left({x}−{y}\right)^{\mathrm{2}} \:=\frac{\mathrm{18}}{\mathrm{7}}\:\:\:\:\:\:\:\:\:\:\:\:.....\left({f}\right) \\ $$$${squaring}\:{and}\:{adding}\:{eqns}.\:\left({a}\right),\left({b}\right), \\ $$$${and}\:\left({c}\right)\:{we}\:{get} \\ $$$$\left({x}+{y}+{z}\right)^{\mathrm{2}} ×\mathrm{28}\:=\mathrm{9}+\mathrm{25}+\mathrm{64}\:=\mathrm{98} \\ $$$${or}\:\:\left({x}+{y}+{z}\right)^{\mathrm{2}} =\frac{\mathrm{7}}{\mathrm{2}}\:\:\:\:\:\:\:\:\:\:\:\:.....\left({g}\right) \\ $$$${From}\:\:\left({d}\right)\:{and}\:\left({e}\right): \\ $$$$\:\left({y}−{z}\right)=\frac{\mathrm{5}}{\mathrm{3}}\left({x}−{y}\right)\:\:\:{and} \\ $$$$\:\left({z}−{x}\right)=\frac{−\mathrm{8}}{\mathrm{3}}\left({x}−{y}\right) \\ $$$${we}\:{get}\:\:\:\:\mathrm{5}{x}−\mathrm{8}{y}\:+\mathrm{3}{z}\:=\mathrm{0}\:\:\:\:\:\:\:...\left({h}\right) \\ $$$$\:{From}\:\left({g}\right)\:,\:\:{If}\:\:{x}+{y}+{z}\:=+\frac{\sqrt{\mathrm{7}}}{\sqrt{\mathrm{2}}} \\ $$$${using}\:{this}\:{in}\:\left({a}\right), \\ $$$$\:\:\:\:{y}−{x}\:=\:\frac{\mathrm{3}\sqrt{\mathrm{2}}}{\sqrt{\mathrm{7}}}\:\:\:\:,\:{and}\:{using}\:{it}\:{in}\left({b}\right) \\ $$$$\:\:\:\:{z}−{y}\:=\:\frac{\mathrm{5}\sqrt{\mathrm{2}}}{\sqrt{\mathrm{7}}}\:\:,\:{and}\:{in}\:\left({c}\right)\:{to}\:{get} \\ $$$$\:\:\:\:{x}−{z}\:=\:\frac{−\mathrm{8}\sqrt{\mathrm{2}}}{\sqrt{\mathrm{7}}}\:\:. \\ $$$$\:\:\:\:\:{x}+{y}+{z}\:=\:\frac{\sqrt{\mathrm{7}}}{\sqrt{\mathrm{2}}} \\ $$$$\Rightarrow\:\:{x}+\left({x}+\frac{\mathrm{3}\sqrt{\mathrm{2}}}{\sqrt{\mathrm{7}}}\right)+\left({x}+\frac{\mathrm{8}\sqrt{\mathrm{2}}}{\sqrt{\mathrm{7}}}\right)=\frac{\sqrt{\mathrm{7}}}{\sqrt{\mathrm{2}}} \\ $$$$\Rightarrow\:\:\mathrm{3}{x}\:=\frac{\sqrt{\mathrm{7}}}{\sqrt{\mathrm{2}}}−\frac{\mathrm{11}\sqrt{\mathrm{2}}}{\sqrt{\mathrm{7}}}\:=\:−\frac{\mathrm{15}}{\sqrt{\mathrm{14}}} \\ $$$${or}\:\:\:\:\boldsymbol{{x}}\:=−\:\frac{\mathrm{5}}{\sqrt{\mathrm{14}}} \\ $$$$\:\:\:\:\:\:\:\:\:\boldsymbol{{y}}\:=\:\boldsymbol{{x}}+\frac{\mathrm{3}\sqrt{\mathrm{2}}}{\sqrt{\mathrm{7}}}\:=\:−\frac{\mathrm{5}}{\sqrt{\mathrm{14}}}+\frac{\mathrm{6}}{\sqrt{\mathrm{14}}} \\ $$$$\:\:\:\:\:\:\boldsymbol{{or}}\:\:\boldsymbol{{y}}=\:\frac{\mathrm{1}}{\sqrt{\mathrm{14}}}\:\:\:\:{and} \\ $$$$\:\:\:\:\:\:\:\boldsymbol{{z}}\:=\boldsymbol{{x}}+\frac{\mathrm{8}\sqrt{\mathrm{2}}}{\sqrt{\mathrm{7}}}\:=\:\frac{−\mathrm{5}}{\sqrt{\mathrm{14}}}+\frac{\mathrm{16}}{\sqrt{\mathrm{14}}} \\ $$$$\:\:\:\:\:\:\:\boldsymbol{{or}}\:\:\boldsymbol{{z}}\:=\:\frac{\mathrm{11}}{\sqrt{\mathrm{14}}}\:. \\ $$$$\boldsymbol{{S}}{o}\:{one}\:{solution}\:{is} \\ $$$$\:\:\:\:\:\:\left(\frac{−\mathrm{5}}{\sqrt{\mathrm{14}}}\:,\:\frac{\mathrm{1}}{\sqrt{\mathrm{14}}}\:,\:\frac{\mathrm{11}}{\sqrt{\mathrm{14}}}\right)\:\:\:\:\:\left({Answer}\right). \\ $$$${and}\:{to}\:{get}\:{the}\:{other}\:{one} \\ $$$${we}\:{shall}\:{take}\:\:\:\:{x}+{y}+{z}\:=\:−\frac{\sqrt{\mathrm{7}}}{\sqrt{\mathrm{2}}} \\ $$$$\Rightarrow\:\:\:\mathrm{3}{x}−\frac{\mathrm{3}\sqrt{\mathrm{2}}}{\sqrt{\mathrm{7}}}−\frac{\mathrm{8}\sqrt{\mathrm{2}}}{\sqrt{\mathrm{7}}}\:=\frac{−\sqrt{\mathrm{7}}}{\sqrt{\mathrm{2}}} \\ $$$$\Rightarrow\:\:\:{x}=\:\frac{\mathrm{1}}{\mathrm{3}}\left(\frac{\mathrm{22}}{\sqrt{\mathrm{14}}}−\frac{\mathrm{7}}{\sqrt{\mathrm{14}}}\right)\:\:=\:\frac{\mathrm{5}}{\mathrm{3}\sqrt{\mathrm{14}}} \\ $$$$\:\:\:\:{y}={x}−\frac{\mathrm{3}\sqrt{\mathrm{2}}}{\sqrt{\mathrm{7}}}\:=\:\frac{−\mathrm{13}}{\mathrm{3}\sqrt{\mathrm{14}}}\:\:\:{and}\: \\ $$$$\:\:\:\:\:{z}\:=\:{x}−\frac{\mathrm{8}\sqrt{\mathrm{2}}}{\sqrt{\mathrm{7}}}\:=\:\frac{−\mathrm{43}}{\mathrm{3}\sqrt{\mathrm{14}}}\: \\ $$$${so}\:{other}\:{solution}\:{is} \\ $$$$\:\:\:\:\:\left(\frac{\mathrm{5}}{\mathrm{3}\sqrt{\mathrm{14}}}\:,\:\frac{−\mathrm{13}}{\mathrm{3}\sqrt{\mathrm{14}}}\:,\:\frac{−\mathrm{43}}{\mathrm{3}\sqrt{\mathrm{14}}}\:\right)\:. \\ $$$${this}\:{one}\:{dont}\:{seem}\:{to}\:{agree}...?! \\ $$
Commented by Rasheed.Sindhi last updated on 04/Nov/17

$$\mathcal{V}\:\mathcal{N}\mathfrak{ice}\:\mathcal{S}\mathfrak{ir}! \\ $$
Commented by tawa tawa last updated on 05/Nov/17

$$\mathrm{God}\:\mathrm{bless}\:\mathrm{you}\:\mathrm{sir}.\:\mathrm{I}\:\mathrm{really}\:\mathrm{appreciate}.\: \\ $$
