
Question Number 17989 by alex041103 last updated on 13/Jul/17

$${Solve}\:{for}\:{x} \\ $$$${x}^{{x}^{{x}^{{x}^{....} } } } =\:\mathrm{4} \\ $$
Commented by alex041103 last updated on 13/Jul/17

$${just}\:{for}\:{fun} \\ $$
Commented by mrW1 last updated on 13/Jul/17

$$\mathrm{x}^{\mathrm{4}} =\mathrm{4} \\ $$$$\mathrm{x}=\:^{\mathrm{4}} \sqrt{\mathrm{4}}=\sqrt{\mathrm{2}} \\ $$
Commented by alex041103 last updated on 13/Jul/17

$${good} \\ $$
Commented by mrW1 last updated on 13/Jul/17

$$\left(\sqrt{\mathrm{2}}\right)^{\left(\sqrt{\mathrm{2}}\right)^{\left(\sqrt{\mathrm{2}}\right)^{\left(.....\right)} } } =? \\ $$
Commented by mrW1 last updated on 13/Jul/17
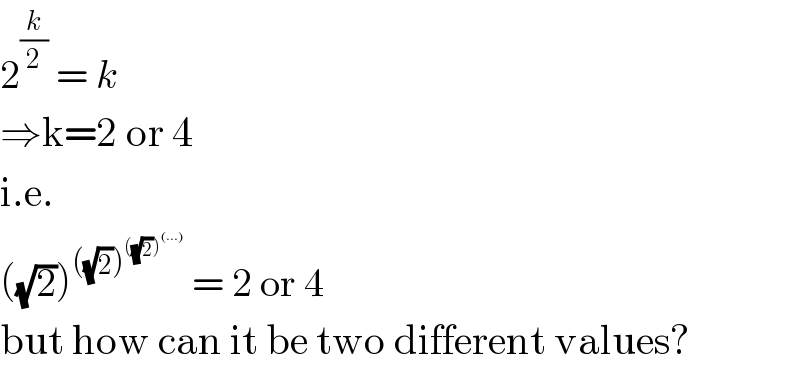
$$\mathrm{2}^{\frac{{k}}{\mathrm{2}}} \:=\:{k} \\ $$$$\Rightarrow\mathrm{k}=\mathrm{2}\:\mathrm{or}\:\mathrm{4} \\ $$$$\mathrm{i}.\mathrm{e}. \\ $$$$\left(\sqrt{\mathrm{2}}\right)^{\left(\sqrt{\mathrm{2}}\right)^{\left(\sqrt{\mathrm{2}}\right)^{\left(...\right)} } } \:=\:\mathrm{2}\:\mathrm{or}\:\mathrm{4} \\ $$$$\mathrm{but}\:\mathrm{how}\:\mathrm{can}\:\mathrm{it}\:\mathrm{be}\:\mathrm{two}\:\mathrm{different}\:\mathrm{values}? \\ $$
Commented by alex041103 last updated on 13/Jul/17
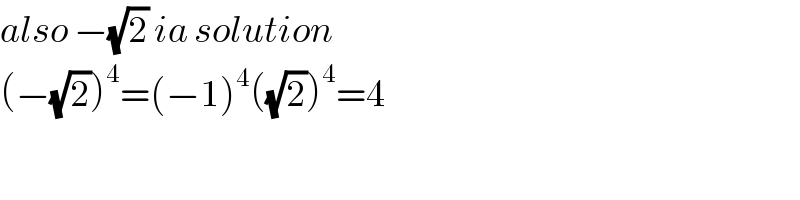
$${also}\:−\sqrt{\mathrm{2}}\:{ia}\:{solution} \\ $$$$\left(−\sqrt{\mathrm{2}}\right)^{\mathrm{4}} =\left(−\mathrm{1}\right)^{\mathrm{4}} \left(\sqrt{\mathrm{2}}\right)^{\mathrm{4}} =\mathrm{4} \\ $$
Commented by prakash jain last updated on 13/Jul/17

$${x}^{{x}^{{x}^{\iddots\infty} } } =\mathrm{4} \\ $$$$\sqrt{\mathrm{2}}\:\mathrm{is}\:\mathrm{not}\:\mathrm{a}\:\mathrm{valid}\:\mathrm{solution}. \\ $$
Commented by alex041103 last updated on 13/Jul/17

$${True} \\ $$
