
Question Number 106188 by mr W last updated on 03/Aug/20
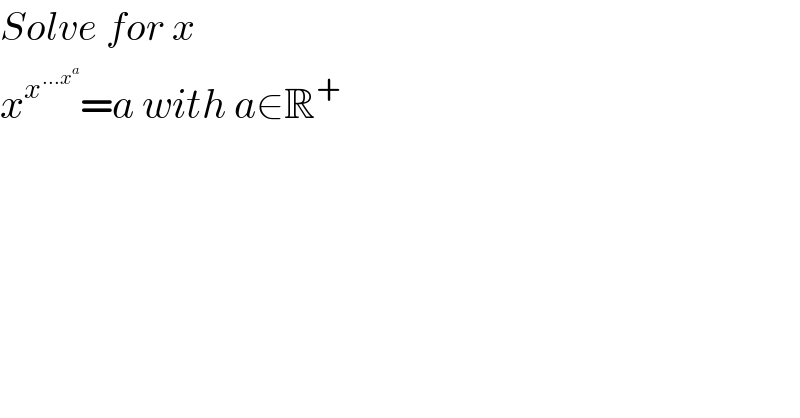
$${Solve}\:{for}\:{x} \\ $$$${x}^{{x}^{...{x}^{{a}} } } ={a}\:{with}\:{a}\in\mathbb{R}^{+} \\ $$
Answered by Dwaipayan Shikari last updated on 03/Aug/20
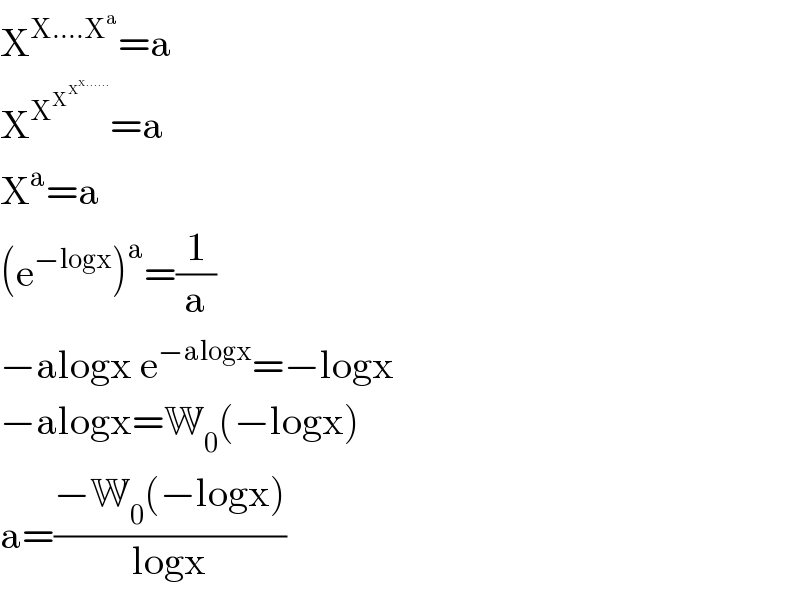
$$\mathrm{X}^{\mathrm{X}....\mathrm{X}^{\mathrm{a}} } =\mathrm{a} \\ $$$$\mathrm{X}^{\mathrm{X}^{\mathrm{X}^{\mathrm{X}^{\mathrm{X}......} } } } =\mathrm{a} \\ $$$$\mathrm{X}^{\mathrm{a}} =\mathrm{a} \\ $$$$\left(\mathrm{e}^{−\mathrm{logx}} \right)^{\mathrm{a}} =\frac{\mathrm{1}}{\mathrm{a}} \\ $$$$−\mathrm{alogx}\:\mathrm{e}^{−\mathrm{alogx}} =−\mathrm{logx} \\ $$$$−\mathrm{alogx}=\mathbb{W}_{\mathrm{0}} \left(−\mathrm{logx}\right) \\ $$$$\mathrm{a}=\frac{−\mathbb{W}_{\mathrm{0}} \left(−\mathrm{logx}\right)}{\mathrm{logx}} \\ $$
Commented by mr W last updated on 03/Aug/20

$${we}\:{should}\:{solve}\:{for}\:{x},\:{not}\:{for}\:{a}. \\ $$$$ \\ $$$${please}\:{compare}\:{following}\:{cases}: \\ $$$${x}^{{x}^{\frac{\mathrm{1}}{\mathrm{2}}} } =\frac{\mathrm{1}}{\mathrm{2}} \\ $$$${x}^{{x}^{{x}^{\frac{\mathrm{1}}{\mathrm{2}}} } } =\frac{\mathrm{1}}{\mathrm{2}} \\ $$
Commented by Dwaipayan Shikari last updated on 03/Aug/20

$${X}^{{X}^{{X}..{A}} } ={A} \\ $$$${X}^{{X}..{A}} ={A} \\ $$$${X}^{{X}^{{X}^{{X}^{{X}.....} } } } ={A} \\ $$$${X}^{{A}} ={A} \\ $$$${X}=\sqrt[{{A}}]{{A}} \\ $$$${I}\:{think}\:{that}\:{two}\:{following}\:{cases}\:{are}\:{same} \\ $$
Answered by mr W last updated on 03/Aug/20
![we see the root of x^a =a is also a root of the original equation. from x^a =a we get x=a^(1/a) , i.e. the original equation has at least a root x=a^(1/a) . but does the original equation have more than this root? case 1: x^x^(...x^a ) =a with odd number of x in the equation. we see the original equation is equivalent to x^a =a, that means the root x=a^(1/a) is the only one root of the original equation. case 2: x^x^(...x^a ) =a with even number of x in the equation. we see the original equation is equivalent to x^x^a =a. we can solve it as following: x^a ln x=ln a x^a ln x^a =aln a (ln x^a )e^((ln x^a )) =aln a ⇒ln x^a =W(aln a) ⇒x=[e^(W(aln a)) ]^(1/a) =[((aln a)/(W(aln a)))]^(1/a) for a=1 ⇒we see x=1 for a>1 ⇒ aln a>0 ⇒we get one root for a<1 ⇒ −(1/e)≤aln a<0 ⇒we get two roots (if a≠(1/e))or one root (if a=(1/e)).](Q106244.png)
$${we}\:{see}\:{the}\:{root}\:{of}\:{x}^{{a}} ={a}\:{is}\:{also}\:{a}\:{root} \\ $$$${of}\:{the}\:{original}\:{equation}. \\ $$$${from}\:{x}^{{a}} ={a}\:{we}\:{get}\:{x}={a}^{\frac{\mathrm{1}}{{a}}} ,\:{i}.{e}.\:{the} \\ $$$${original}\:{equation}\:{has}\:{at}\:{least}\:{a}\:{root} \\ $$$${x}={a}^{\frac{\mathrm{1}}{{a}}} . \\ $$$$ \\ $$$${but}\:{does}\:{the}\:{original}\:{equation}\:{have} \\ $$$${more}\:{than}\:{this}\:{root}? \\ $$$${case}\:\mathrm{1}:\:{x}^{{x}^{...{x}^{{a}} } } ={a}\:{with}\:{odd}\:{number}\:{of} \\ $$$${x}\:{in}\:{the}\:{equation}. \\ $$$${we}\:{see}\:{the}\:{original}\:{equation}\:{is} \\ $$$${equivalent}\:{to}\:{x}^{{a}} ={a},\:{that}\:{means}\:{the} \\ $$$${root}\:{x}={a}^{\frac{\mathrm{1}}{{a}}} \:{is}\:{the}\:{only}\:{one}\:{root}\:{of} \\ $$$${the}\:{original}\:{equation}. \\ $$$$ \\ $$$${case}\:\mathrm{2}:\:{x}^{{x}^{...{x}^{{a}} } } ={a}\:{with}\:{even}\:{number}\:{of} \\ $$$${x}\:{in}\:{the}\:{equation}. \\ $$$${we}\:{see}\:{the}\:{original}\:{equation}\:{is} \\ $$$${equivalent}\:{to}\:{x}^{{x}^{{a}} } ={a}.\:{we}\:{can}\:{solve}\:{it} \\ $$$${as}\:{following}: \\ $$$${x}^{{a}} \mathrm{ln}\:{x}=\mathrm{ln}\:{a} \\ $$$${x}^{{a}} \mathrm{ln}\:{x}^{{a}} ={a}\mathrm{ln}\:{a} \\ $$$$\left(\mathrm{ln}\:{x}^{{a}} \right){e}^{\left(\mathrm{ln}\:{x}^{{a}} \right)} ={a}\mathrm{ln}\:{a} \\ $$$$\Rightarrow\mathrm{ln}\:{x}^{{a}} ={W}\left({a}\mathrm{ln}\:{a}\right) \\ $$$$\Rightarrow{x}=\left[{e}^{{W}\left({a}\mathrm{ln}\:{a}\right)} \right]^{\frac{\mathrm{1}}{{a}}} =\left[\frac{{a}\mathrm{ln}\:{a}}{{W}\left({a}\mathrm{ln}\:{a}\right)}\right]^{\frac{\mathrm{1}}{{a}}} \\ $$$${for}\:{a}=\mathrm{1}\:\Rightarrow{we}\:{see}\:{x}=\mathrm{1} \\ $$$${for}\:{a}>\mathrm{1}\:\Rightarrow\:{a}\mathrm{ln}\:{a}>\mathrm{0}\:\Rightarrow{we}\:{get}\:{one}\:{root} \\ $$$${for}\:{a}<\mathrm{1}\:\Rightarrow\:−\frac{\mathrm{1}}{{e}}\leqslant{a}\mathrm{ln}\:{a}<\mathrm{0}\:\Rightarrow{we}\:{get} \\ $$$${two}\:{roots}\:\left({if}\:{a}\neq\frac{\mathrm{1}}{{e}}\right){or}\:{one}\:{root}\:\left({if}\:{a}=\frac{\mathrm{1}}{{e}}\right). \\ $$
