Question and Answers Forum

All Questions      Topic List

Algebra Questions

Previous in All Question      Next in All Question      

Previous in Algebra      Next in Algebra      

Question Number 208164 by Fridunatjan08 last updated on 06/Jun/24

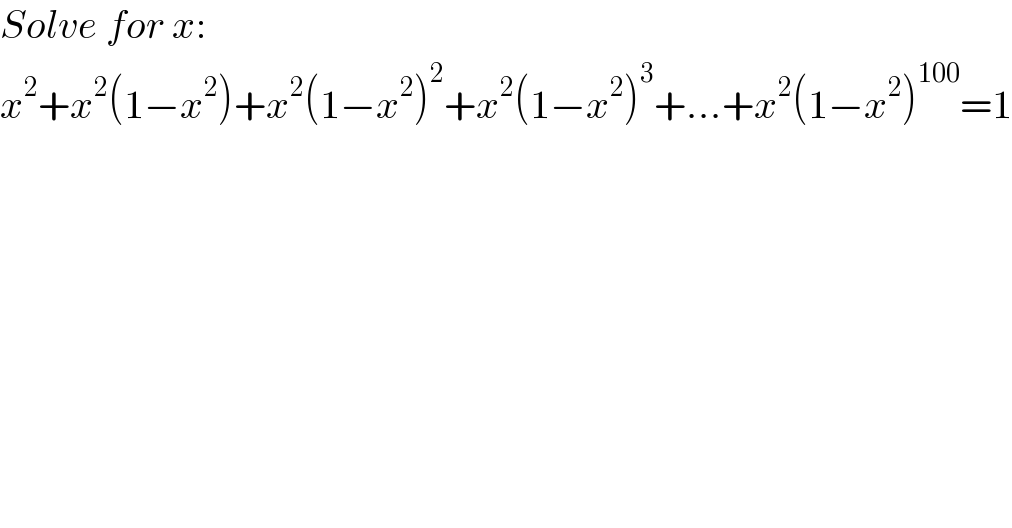
Solve for x: x^2 +x^2 (1−x^2 )+x^2 (1−x^2 )^2 +x^2 (1−x^2 )^3 +...+x^2 (1−x^2 )^(100) =1

$${Solve}\:{for}\:{x}: \\ $$$${x}^{\mathrm{2}} +{x}^{\mathrm{2}} \left(\mathrm{1}−{x}^{\mathrm{2}} \right)+{x}^{\mathrm{2}} \left(\mathrm{1}−{x}^{\mathrm{2}} \right)^{\mathrm{2}} +{x}^{\mathrm{2}} \left(\mathrm{1}−{x}^{\mathrm{2}} \right)^{\mathrm{3}} +...+{x}^{\mathrm{2}} \left(\mathrm{1}−{x}^{\mathrm{2}} \right)^{\mathrm{100}} =\mathrm{1} \\ $$

Answered by A5T last updated on 06/Jun/24

x^2 +x^2 (1−x^2 )+x^2 (1−x^2 )^2 +...+x^2 (1−x^2 )^(100) =1 ⇒x^2 (1−x^2 )+x^2 (1−x^2 )^2 +...+x^2 (1−x^2 )^(100) =1−x^2 Dividing through by 1−x^2 [x≠+_− 1] ⇒x^2 +x^2 (1−x^2 )+x^2 (1−x^2 )^2 +...+x^2 (1−x^2 )^(99) =1 Subtracting x^2 from both sides, dividing by (1−x^2 ) and iterating ⇒x^2 (1−x^2 )=1−x^2 ⇒x^2 =1⇒x=+_− 1 But by assumption that x≠+_− 1 initially ⇒x=+_− 1

$${x}^{\mathrm{2}} +{x}^{\mathrm{2}} \left(\mathrm{1}−{x}^{\mathrm{2}} \right)+{x}^{\mathrm{2}} \left(\mathrm{1}−{x}^{\mathrm{2}} \right)^{\mathrm{2}} +...+{x}^{\mathrm{2}} \left(\mathrm{1}−{x}^{\mathrm{2}} \right)^{\mathrm{100}} =\mathrm{1} \\ $$$$\Rightarrow{x}^{\mathrm{2}} \left(\mathrm{1}−{x}^{\mathrm{2}} \right)+{x}^{\mathrm{2}} \left(\mathrm{1}−{x}^{\mathrm{2}} \right)^{\mathrm{2}} +...+{x}^{\mathrm{2}} \left(\mathrm{1}−{x}^{\mathrm{2}} \right)^{\mathrm{100}} =\mathrm{1}−{x}^{\mathrm{2}} \\ $$$${Dividing}\:{through}\:{by}\:\mathrm{1}−{x}^{\mathrm{2}} \:\left[{x}\neq\underset{−} {+}\mathrm{1}\right] \\ $$$$\Rightarrow{x}^{\mathrm{2}} +{x}^{\mathrm{2}} \left(\mathrm{1}−{x}^{\mathrm{2}} \right)+{x}^{\mathrm{2}} \left(\mathrm{1}−{x}^{\mathrm{2}} \right)^{\mathrm{2}} +...+{x}^{\mathrm{2}} \left(\mathrm{1}−{x}^{\mathrm{2}} \right)^{\mathrm{99}} =\mathrm{1} \\ $$$${Subtracting}\:\:{x}^{\mathrm{2}} \:{from}\:{both}\:{sides},\:{dividing}\:{by}\: \\ $$$$\left(\mathrm{1}−{x}^{\mathrm{2}} \right)\:{and}\:{iterating} \\ $$$$\Rightarrow{x}^{\mathrm{2}} \left(\mathrm{1}−{x}^{\mathrm{2}} \right)=\mathrm{1}−{x}^{\mathrm{2}} \Rightarrow{x}^{\mathrm{2}} =\mathrm{1}\Rightarrow{x}=\underset{−} {+}\mathrm{1} \\ $$$${But}\:{by}\:{assumption}\:{that}\:{x}\neq\underset{−} {+}\mathrm{1}\:{initially} \\ $$$$\Rightarrow{x}=\underset{−} {+}\mathrm{1} \\ $$

Commented by Fridunatjan08 last updated on 07/Jun/24

thanks sir.

$${thanks}\:{sir}. \\ $$

Answered by Berbere last updated on 07/Jun/24

x^2 (Σ_(k=0) ^(100) (1−x^2 )^k )=1⇒x≠0 x^2 .((1−(1−x^2 )^(101) )/x^2 )=1 ⇔1−(1−x^2 )^(101) =1⇒x^2 =1⇒x∈{−1,1}

$${x}^{\mathrm{2}} \left(\underset{{k}=\mathrm{0}} {\overset{\mathrm{100}} {\sum}}\left(\mathrm{1}−{x}^{\mathrm{2}} \right)^{{k}} \right)=\mathrm{1}\Rightarrow{x}\neq\mathrm{0} \\ $$$${x}^{\mathrm{2}} .\frac{\mathrm{1}−\left(\mathrm{1}−{x}^{\mathrm{2}} \right)^{\mathrm{101}} }{{x}^{\mathrm{2}} }=\mathrm{1} \\ $$$$\Leftrightarrow\mathrm{1}−\left(\mathrm{1}−{x}^{\mathrm{2}} \right)^{\mathrm{101}} =\mathrm{1}\Rightarrow{x}^{\mathrm{2}} =\mathrm{1}\Rightarrow{x}\in\left\{−\mathrm{1},\mathrm{1}\right\} \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com