
Question Number 21082 by chernoaguero@gmail.com last updated on 12/Sep/17
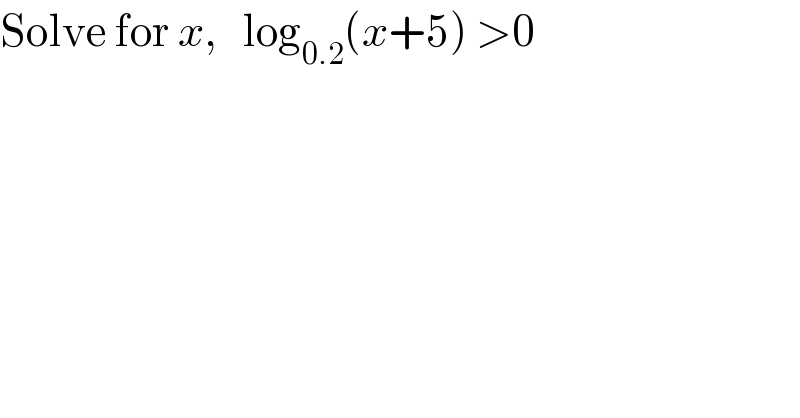
$$\mathrm{Solve}\:\mathrm{for}\:{x},\:\:\:\mathrm{log}_{\mathrm{0}.\mathrm{2}} \left({x}+\mathrm{5}\right)\:>\mathrm{0} \\ $$
Answered by mrW1 last updated on 12/Sep/17
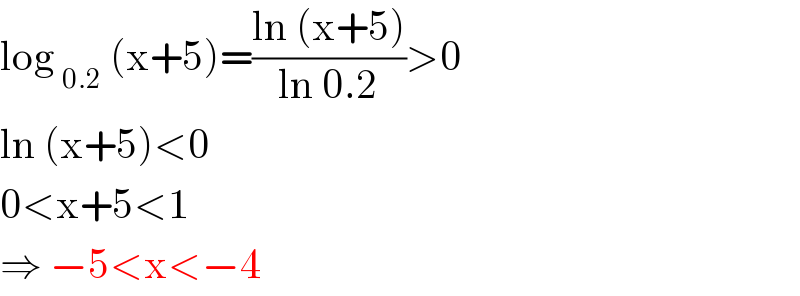
$$\mathrm{log}\:_{\mathrm{0}.\mathrm{2}} \:\left(\mathrm{x}+\mathrm{5}\right)=\frac{\mathrm{ln}\:\left(\mathrm{x}+\mathrm{5}\right)}{\mathrm{ln}\:\mathrm{0}.\mathrm{2}}>\mathrm{0} \\ $$$$\mathrm{ln}\:\left(\mathrm{x}+\mathrm{5}\right)<\mathrm{0} \\ $$$$\mathrm{0}<\mathrm{x}+\mathrm{5}<\mathrm{1} \\ $$$$\Rightarrow\:−\mathrm{5}<\mathrm{x}<−\mathrm{4} \\ $$
Commented by chernoaguero@gmail.com last updated on 12/Sep/17

$${Thank}\:{you} \\ $$
