
Question Number 11263 by tawa last updated on 18/Mar/17
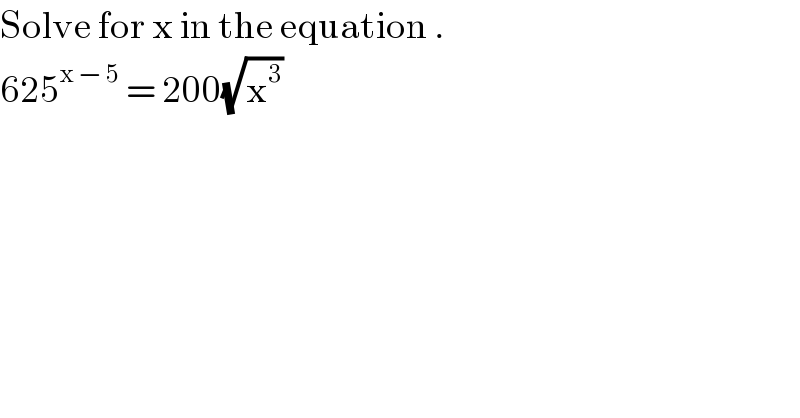
$$\mathrm{Solve}\:\mathrm{for}\:\mathrm{x}\:\mathrm{in}\:\mathrm{the}\:\mathrm{equation}\:. \\ $$$$\mathrm{625}^{\mathrm{x}\:−\:\mathrm{5}} \:=\:\mathrm{200}\sqrt{\mathrm{x}^{\mathrm{3}} } \\ $$
Answered by ajfour last updated on 18/Mar/17
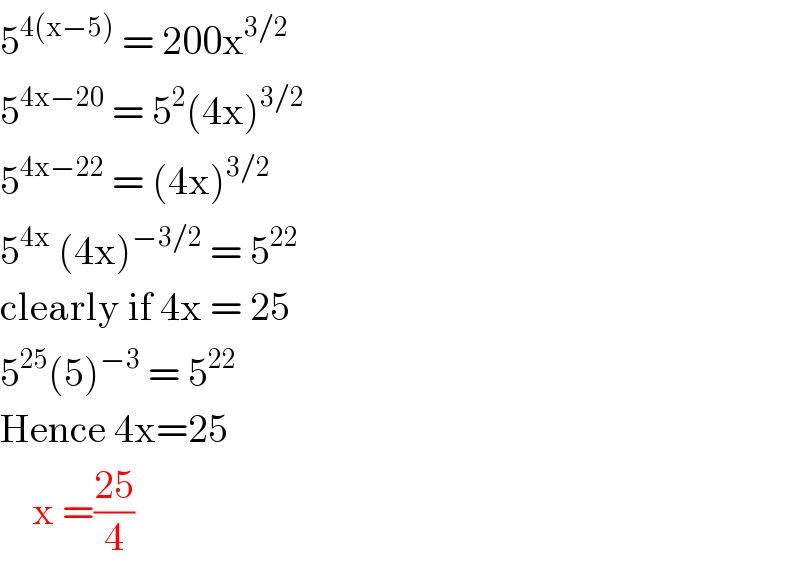
$$\mathrm{5}^{\mathrm{4}\left(\mathrm{x}−\mathrm{5}\right)} \:=\:\mathrm{200x}^{\mathrm{3}/\mathrm{2}} \\ $$$$\mathrm{5}^{\mathrm{4x}−\mathrm{20}} \:=\:\mathrm{5}^{\mathrm{2}} \left(\mathrm{4x}\right)^{\mathrm{3}/\mathrm{2}} \\ $$$$\mathrm{5}^{\mathrm{4x}−\mathrm{22}} \:=\:\left(\mathrm{4x}\right)^{\mathrm{3}/\mathrm{2}} \\ $$$$\mathrm{5}^{\mathrm{4x}} \:\left(\mathrm{4x}\right)^{−\mathrm{3}/\mathrm{2}} \:=\:\mathrm{5}^{\mathrm{22}} \\ $$$$\mathrm{clearly}\:\mathrm{if}\:\mathrm{4x}\:=\:\mathrm{25} \\ $$$$\mathrm{5}^{\mathrm{25}} \left(\mathrm{5}\right)^{−\mathrm{3}} \:=\:\mathrm{5}^{\mathrm{22}} \\ $$$$\mathrm{Hence}\:\mathrm{4x}=\mathrm{25} \\ $$$$\:\:\:\:\mathrm{x}\:=\frac{\mathrm{25}}{\mathrm{4}}\:\: \\ $$
