Question and Answers Forum

All Questions      Topic List

Algebra Questions

Previous in All Question      Next in All Question      

Previous in Algebra      Next in Algebra      

Question Number 216010 by MATHEMATICSAM last updated on 25/Jan/25

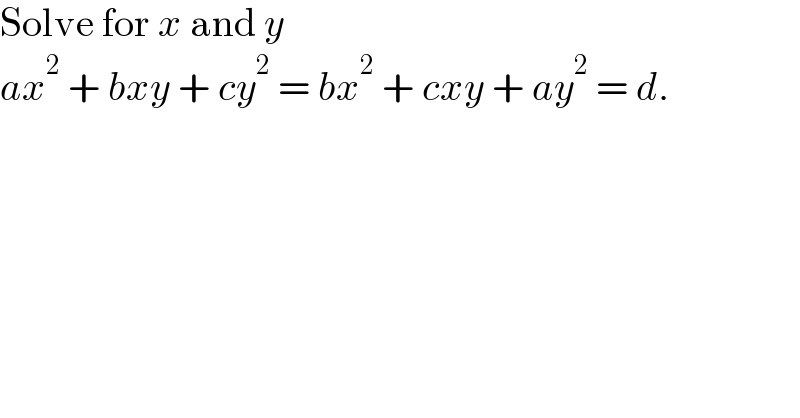
Solve for x and y ax^2 + bxy + cy^2 = bx^2 + cxy + ay^2 = d.

$$\mathrm{Solve}\:\mathrm{for}\:{x}\:\mathrm{and}\:{y} \\ $$$${ax}^{\mathrm{2}} \:+\:{bxy}\:+\:{cy}^{\mathrm{2}} \:=\:{bx}^{\mathrm{2}} \:+\:{cxy}\:+\:{ay}^{\mathrm{2}} \:=\:{d}. \\ $$

Answered by mr W last updated on 26/Jan/25

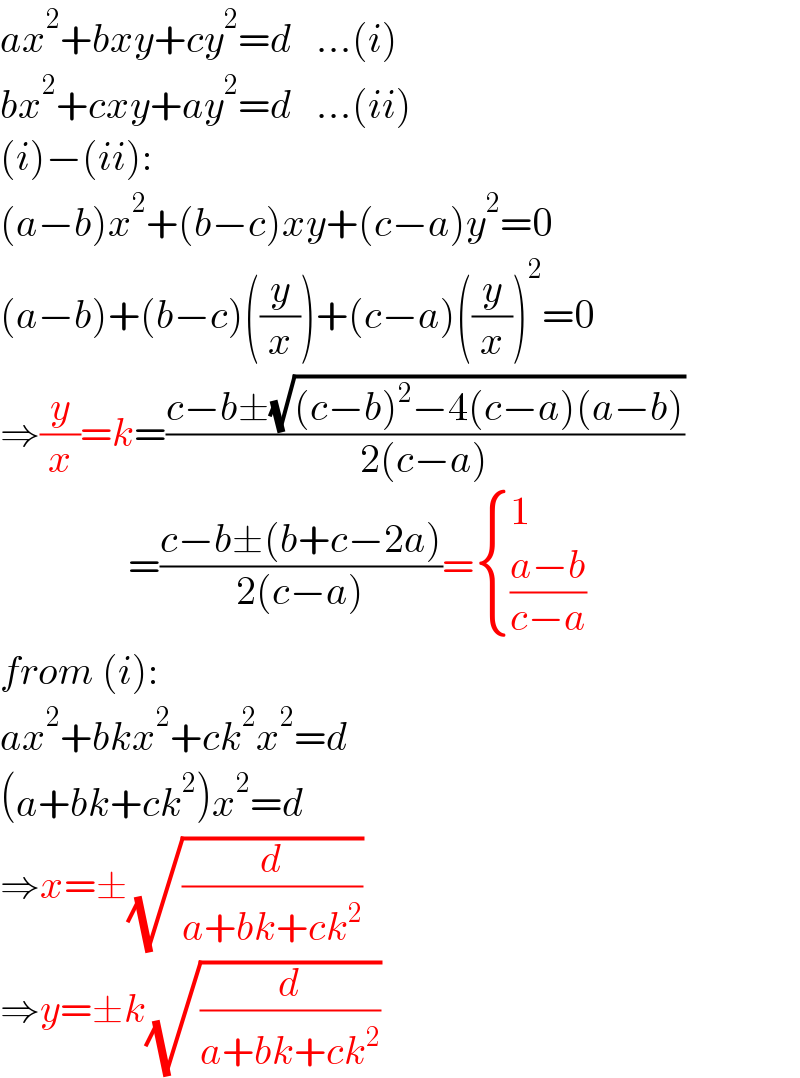
ax^2 +bxy+cy^2 =d ...(i) bx^2 +cxy+ay^2 =d ...(ii) (i)−(ii): (a−b)x^2 +(b−c)xy+(c−a)y^2 =0 (a−b)+(b−c)((y/x))+(c−a)((y/x))^2 =0 ⇒(y/x)=k=((c−b±(√((c−b)^2 −4(c−a)(a−b))))/(2(c−a))) =((c−b±(b+c−2a))/(2(c−a)))= { (1),(((a−b)/(c−a))) :} from (i): ax^2 +bkx^2 +ck^2 x^2 =d (a+bk+ck^2 )x^2 =d ⇒x=±(√(d/(a+bk+ck^2 ))) ⇒y=±k(√(d/(a+bk+ck^2 )))

$${ax}^{\mathrm{2}} +{bxy}+{cy}^{\mathrm{2}} ={d}\:\:\:...\left({i}\right) \\ $$$${bx}^{\mathrm{2}} +{cxy}+{ay}^{\mathrm{2}} ={d}\:\:\:...\left({ii}\right) \\ $$$$\left({i}\right)−\left({ii}\right): \\ $$$$\left({a}−{b}\right){x}^{\mathrm{2}} +\left({b}−{c}\right){xy}+\left({c}−{a}\right){y}^{\mathrm{2}} =\mathrm{0} \\ $$$$\left({a}−{b}\right)+\left({b}−{c}\right)\left(\frac{{y}}{{x}}\right)+\left({c}−{a}\right)\left(\frac{{y}}{{x}}\right)^{\mathrm{2}} =\mathrm{0} \\ $$$$\Rightarrow\frac{{y}}{{x}}={k}=\frac{{c}−{b}\pm\sqrt{\left({c}−{b}\right)^{\mathrm{2}} −\mathrm{4}\left({c}−{a}\right)\left({a}−{b}\right)}}{\mathrm{2}\left({c}−{a}\right)} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:=\frac{{c}−{b}\pm\left({b}+{c}−\mathrm{2}{a}\right)}{\mathrm{2}\left({c}−{a}\right)}=\begin{cases}{\mathrm{1}}\\{\frac{{a}−{b}}{{c}−{a}}}\end{cases} \\ $$$${from}\:\left({i}\right): \\ $$$${ax}^{\mathrm{2}} +{bkx}^{\mathrm{2}} +{ck}^{\mathrm{2}} {x}^{\mathrm{2}} ={d} \\ $$$$\left({a}+{bk}+{ck}^{\mathrm{2}} \right){x}^{\mathrm{2}} ={d} \\ $$$$\Rightarrow{x}=\pm\sqrt{\frac{{d}}{{a}+{bk}+{ck}^{\mathrm{2}} }} \\ $$$$\Rightarrow{y}=\pm{k}\sqrt{\frac{{d}}{{a}+{bk}+{ck}^{\mathrm{2}} }} \\ $$

Answered by Rasheed.Sindhi last updated on 26/Jan/25

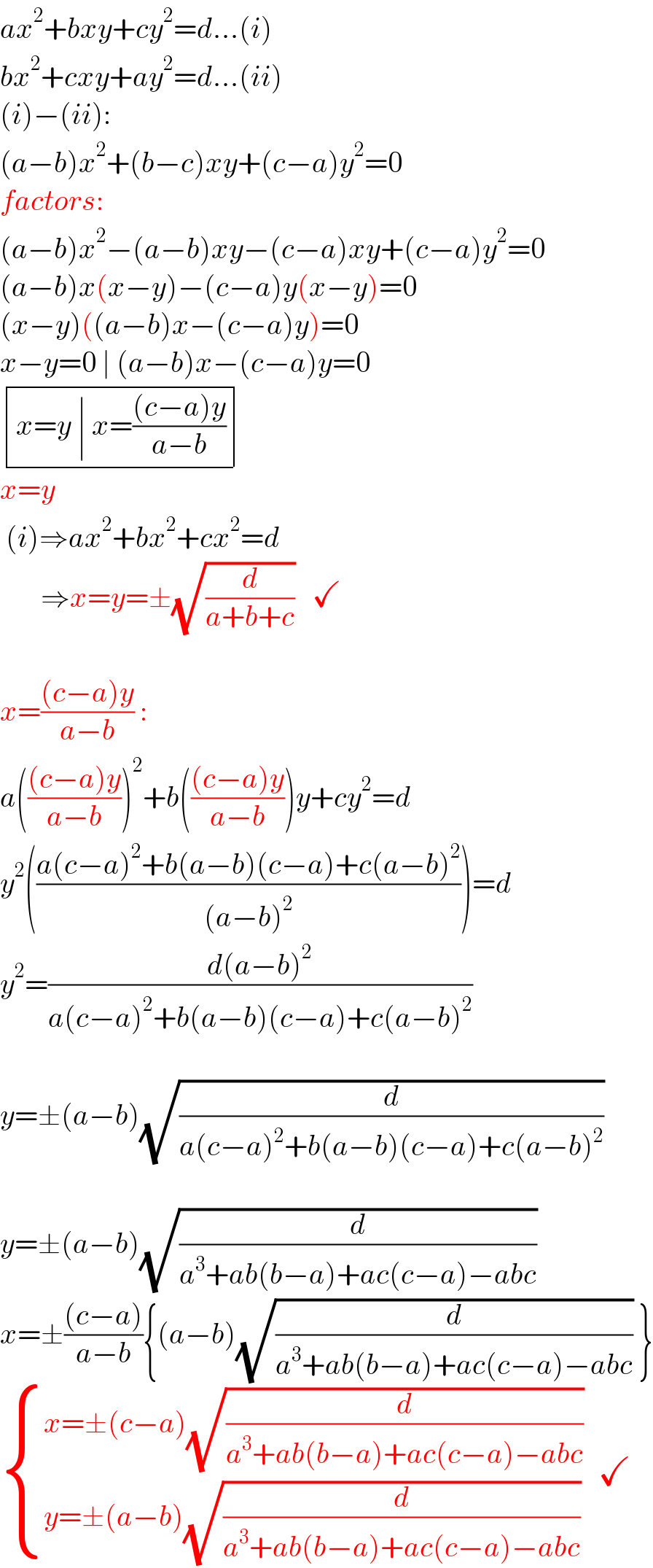
ax^2 +bxy+cy^2 =d...(i) bx^2 +cxy+ay^2 =d...(ii) (i)−(ii): (a−b)x^2 +(b−c)xy+(c−a)y^2 =0 factors: (a−b)x^2 −(a−b)xy−(c−a)xy+(c−a)y^2 =0 (a−b)x(x−y)−(c−a)y(x−y)=0 (x−y)((a−b)x−(c−a)y)=0 x−y=0 ∣ (a−b)x−(c−a)y=0 determinant (((x=y ∣ x=(((c−a)y)/(a−b))))) x=y (i)⇒ax^2 +bx^2 +cx^2 =d ⇒x=y=±(√(d/(a+b+c))) ✓ x=(((c−a)y)/(a−b)) : a((((c−a)y)/(a−b)))^2 +b((((c−a)y)/(a−b)))y+cy^2 =d y^2 (((a(c−a)^2 +b(a−b)(c−a)+c(a−b)^2 )/((a−b)^2 )))=d y^2 =((d(a−b)^2 )/(a(c−a)^2 +b(a−b)(c−a)+c(a−b)^2 )) y=±(a−b)(√(d/(a(c−a)^2 +b(a−b)(c−a)+c(a−b)^2 ))) y=±(a−b)(√(d/(a^3 +ab(b−a)+ac(c−a)−abc))) x=±(((c−a))/(a−b)){(a−b)(√(d/(a^3 +ab(b−a)+ac(c−a)−abc))) } { ((x=±(c−a)(√(d/(a^3 +ab(b−a)+ac(c−a)−abc))))),((y=±(a−b)(√(d/(a^3 +ab(b−a)+ac(c−a)−abc))) )) :} ✓

$${ax}^{\mathrm{2}} +{bxy}+{cy}^{\mathrm{2}} ={d}...\left({i}\right) \\ $$$${bx}^{\mathrm{2}} +{cxy}+{ay}^{\mathrm{2}} ={d}...\left({ii}\right) \\ $$$$\left({i}\right)−\left({ii}\right): \\ $$$$\left({a}−{b}\right){x}^{\mathrm{2}} +\left({b}−{c}\right){xy}+\left({c}−{a}\right){y}^{\mathrm{2}} =\mathrm{0} \\ $$$${factors}: \\ $$$$\left({a}−{b}\right){x}^{\mathrm{2}} −\left({a}−{b}\right){xy}−\left({c}−{a}\right){xy}+\left({c}−{a}\right){y}^{\mathrm{2}} =\mathrm{0} \\ $$$$\left({a}−{b}\right){x}\left({x}−{y}\right)−\left({c}−{a}\right){y}\left({x}−{y}\right)=\mathrm{0} \\ $$$$\left({x}−{y}\right)\left(\left({a}−{b}\right){x}−\left({c}−{a}\right){y}\right)=\mathrm{0} \\ $$$${x}−{y}=\mathrm{0}\:\mid\:\left({a}−{b}\right){x}−\left({c}−{a}\right){y}=\mathrm{0} \\ $$$$\begin{array}{|c|}{{x}={y}\:\mid\:{x}=\frac{\left({c}−{a}\right){y}}{{a}−{b}}}\\\hline\end{array} \\ $$$${x}={y} \\ $$$$\:\left({i}\right)\Rightarrow{ax}^{\mathrm{2}} +{bx}^{\mathrm{2}} +{cx}^{\mathrm{2}} ={d} \\ $$$$\:\:\:\:\:\:\:\Rightarrow{x}={y}=\pm\sqrt{\frac{{d}}{{a}+{b}+{c}}}\:\:\:\checkmark \\ $$$$\: \\ $$$${x}=\frac{\left({c}−{a}\right){y}}{{a}−{b}}\:: \\ $$$${a}\left(\frac{\left({c}−{a}\right){y}}{{a}−{b}}\right)^{\mathrm{2}} +{b}\left(\frac{\left({c}−{a}\right){y}}{{a}−{b}}\right){y}+{cy}^{\mathrm{2}} ={d} \\ $$$${y}^{\mathrm{2}} \left(\frac{{a}\left({c}−{a}\right)^{\mathrm{2}} +{b}\left({a}−{b}\right)\left({c}−{a}\right)+{c}\left({a}−{b}\right)^{\mathrm{2}} }{\left({a}−{b}\right)^{\mathrm{2}} }\right)={d} \\ $$$${y}^{\mathrm{2}} =\frac{{d}\left({a}−{b}\right)^{\mathrm{2}} }{{a}\left({c}−{a}\right)^{\mathrm{2}} +{b}\left({a}−{b}\right)\left({c}−{a}\right)+{c}\left({a}−{b}\right)^{\mathrm{2}} } \\ $$$$\: \\ $$$${y}=\pm\left({a}−{b}\right)\sqrt{\frac{{d}}{{a}\left({c}−{a}\right)^{\mathrm{2}} +{b}\left({a}−{b}\right)\left({c}−{a}\right)+{c}\left({a}−{b}\right)^{\mathrm{2}} }} \\ $$$$\: \\ $$$${y}=\pm\left({a}−{b}\right)\sqrt{\frac{{d}}{{a}^{\mathrm{3}} +{ab}\left({b}−{a}\right)+{ac}\left({c}−{a}\right)−{abc}}} \\ $$$${x}=\pm\frac{\left({c}−{a}\right)}{{a}−{b}}\left\{\left({a}−{b}\right)\sqrt{\frac{{d}}{{a}^{\mathrm{3}} +{ab}\left({b}−{a}\right)+{ac}\left({c}−{a}\right)−{abc}}}\:\right\} \\ $$$$\begin{cases}{{x}=\pm\left({c}−{a}\right)\sqrt{\frac{{d}}{{a}^{\mathrm{3}} +{ab}\left({b}−{a}\right)+{ac}\left({c}−{a}\right)−{abc}}}}\\{{y}=\pm\left({a}−{b}\right)\sqrt{\frac{{d}}{{a}^{\mathrm{3}} +{ab}\left({b}−{a}\right)+{ac}\left({c}−{a}\right)−{abc}}}\:\:}\end{cases}\:\checkmark \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com