
Question Number 209872 by Frix last updated on 24/Jul/24
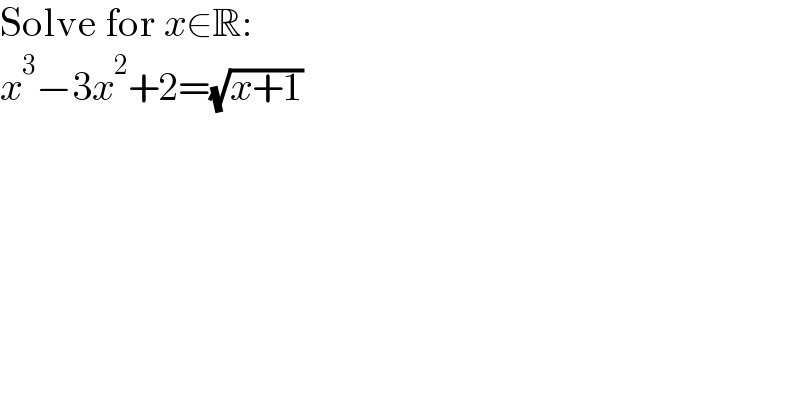
$$\mathrm{Solve}\:\mathrm{for}\:{x}\in\mathbb{R}: \\ $$$${x}^{\mathrm{3}} −\mathrm{3}{x}^{\mathrm{2}} +\mathrm{2}=\sqrt{{x}+\mathrm{1}} \\ $$
Answered by Ghisom last updated on 24/Jul/24
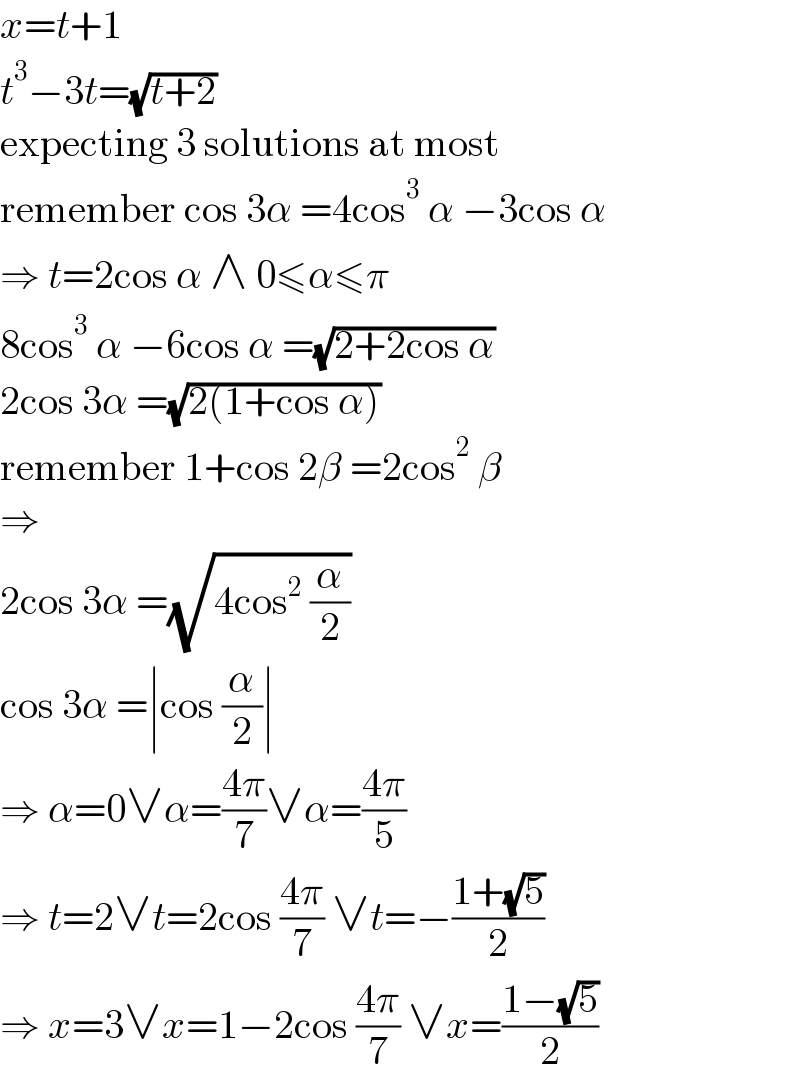
$${x}={t}+\mathrm{1} \\ $$$${t}^{\mathrm{3}} −\mathrm{3}{t}=\sqrt{{t}+\mathrm{2}} \\ $$$$\mathrm{expecting}\:\mathrm{3}\:\mathrm{solutions}\:\mathrm{at}\:\mathrm{most} \\ $$$$\mathrm{remember}\:\mathrm{cos}\:\mathrm{3}\alpha\:=\mathrm{4cos}^{\mathrm{3}} \:\alpha\:−\mathrm{3cos}\:\alpha \\ $$$$\Rightarrow\:{t}=\mathrm{2cos}\:\alpha\:\wedge\:\mathrm{0}\leqslant\alpha\leqslant\pi \\ $$$$\mathrm{8cos}^{\mathrm{3}} \:\alpha\:−\mathrm{6cos}\:\alpha\:=\sqrt{\mathrm{2}+\mathrm{2cos}\:\alpha} \\ $$$$\mathrm{2cos}\:\mathrm{3}\alpha\:=\sqrt{\mathrm{2}\left(\mathrm{1}+\mathrm{cos}\:\alpha\right)} \\ $$$$\mathrm{remember}\:\mathrm{1}+\mathrm{cos}\:\mathrm{2}\beta\:=\mathrm{2cos}^{\mathrm{2}} \:\beta \\ $$$$\Rightarrow \\ $$$$\mathrm{2cos}\:\mathrm{3}\alpha\:=\sqrt{\mathrm{4cos}^{\mathrm{2}} \:\frac{\alpha}{\mathrm{2}}} \\ $$$$\mathrm{cos}\:\mathrm{3}\alpha\:=\mid\mathrm{cos}\:\frac{\alpha}{\mathrm{2}}\mid \\ $$$$\Rightarrow\:\alpha=\mathrm{0}\vee\alpha=\frac{\mathrm{4}\pi}{\mathrm{7}}\vee\alpha=\frac{\mathrm{4}\pi}{\mathrm{5}} \\ $$$$\Rightarrow\:{t}=\mathrm{2}\vee{t}=\mathrm{2cos}\:\frac{\mathrm{4}\pi}{\mathrm{7}}\:\vee{t}=−\frac{\mathrm{1}+\sqrt{\mathrm{5}}}{\mathrm{2}} \\ $$$$\Rightarrow\:{x}=\mathrm{3}\vee{x}=\mathrm{1}−\mathrm{2cos}\:\frac{\mathrm{4}\pi}{\mathrm{7}}\:\vee{x}=\frac{\mathrm{1}−\sqrt{\mathrm{5}}}{\mathrm{2}} \\ $$
Commented by Frix last updated on 24/Jul/24

$$\mathrm{Great}\:\mathrm{idea}! \\ $$
