
Question Number 218093 by ArshadS last updated on 29/Mar/25
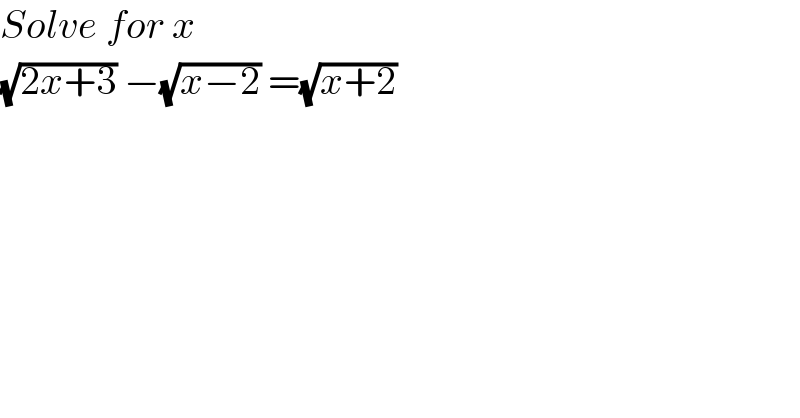
$${Solve}\:{for}\:{x} \\ $$$$\sqrt{\mathrm{2}{x}+\mathrm{3}}\:−\sqrt{{x}−\mathrm{2}}\:=\sqrt{{x}+\mathrm{2}}\: \\ $$
Answered by vnm last updated on 29/Mar/25
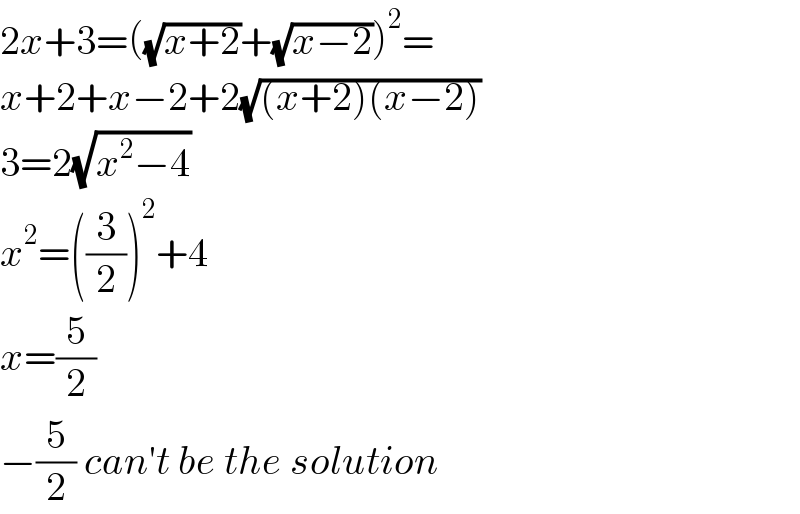
$$\mathrm{2}{x}+\mathrm{3}=\left(\sqrt{{x}+\mathrm{2}}+\sqrt{{x}−\mathrm{2}}\right)^{\mathrm{2}} = \\ $$$${x}+\mathrm{2}+{x}−\mathrm{2}+\mathrm{2}\sqrt{\left({x}+\mathrm{2}\right)\left({x}−\mathrm{2}\right)} \\ $$$$\mathrm{3}=\mathrm{2}\sqrt{{x}^{\mathrm{2}} −\mathrm{4}} \\ $$$${x}^{\mathrm{2}} =\left(\frac{\mathrm{3}}{\mathrm{2}}\right)^{\mathrm{2}} +\mathrm{4} \\ $$$${x}=\frac{\mathrm{5}}{\mathrm{2}} \\ $$$$−\frac{\mathrm{5}}{\mathrm{2}}\:{can}'{t}\:{be}\:{the}\:{solution} \\ $$
Commented by ArshadS last updated on 29/Mar/25

$${Thank}\:{you}\:{sir} \\ $$
Answered by Marzuk last updated on 30/Mar/25
![(√(2x+3))−(√(x−2))=(√(x+2)) or,(√(2x+3))=(√(x+2))+(√(x−2)) or,2x+3 = x+2+x−2+2(√(x+2)).(√(x−2)) [squaring each side] or,2x+3= 2x+2(√(x+2)).(√(x−2)) or,(√(x^2 −4))= (3/2) or,x^2 =((3/2))^2 +4 or,x^2 = ((25)/4) or, x = (√((25)/4)) ∴ x = (5/2) I didn′t show some steps here.](Q218116.png)
$$\sqrt{\mathrm{2}{x}+\mathrm{3}}−\sqrt{{x}−\mathrm{2}}=\sqrt{{x}+\mathrm{2}} \\ $$$${or},\sqrt{\mathrm{2}{x}+\mathrm{3}}=\sqrt{{x}+\mathrm{2}}+\sqrt{{x}−\mathrm{2}} \\ $$$${or},\mathrm{2}{x}+\mathrm{3}\:=\:{x}+\mathrm{2}+{x}−\mathrm{2}+\mathrm{2}\sqrt{{x}+\mathrm{2}}.\sqrt{{x}−\mathrm{2}}\:\:\left[{squaring}\:{each}\:{side}\right] \\ $$$${or},\mathrm{2}{x}+\mathrm{3}=\:\mathrm{2}{x}+\mathrm{2}\sqrt{{x}+\mathrm{2}}.\sqrt{{x}−\mathrm{2}} \\ $$$${or},\sqrt{{x}^{\mathrm{2}} −\mathrm{4}}=\:\frac{\mathrm{3}}{\mathrm{2}} \\ $$$${or},{x}^{\mathrm{2}} =\left(\frac{\mathrm{3}}{\mathrm{2}}\right)^{\mathrm{2}} +\mathrm{4} \\ $$$${or},{x}^{\mathrm{2}} =\:\frac{\mathrm{25}}{\mathrm{4}} \\ $$$${or},\:{x}\:=\:\sqrt{\frac{\mathrm{25}}{\mathrm{4}}} \\ $$$$\therefore\:{x}\:=\:\frac{\mathrm{5}}{\mathrm{2}}\: \\ $$$${I}\:{didn}'{t}\:{show}\:{some}\:{steps}\:{here}. \\ $$
