
Question Number 140767 by EDWIN88 last updated on 12/May/21
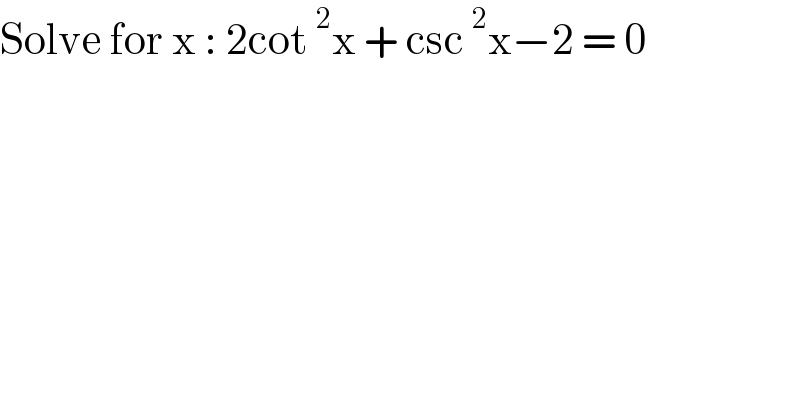
$$\mathrm{Solve}\:\mathrm{for}\:\mathrm{x}\::\:\mathrm{2cot}\:^{\mathrm{2}} \mathrm{x}\:+\:\mathrm{csc}\:^{\mathrm{2}} \mathrm{x}−\mathrm{2}\:=\:\mathrm{0}\: \\ $$
Answered by Ar Brandon last updated on 12/May/21
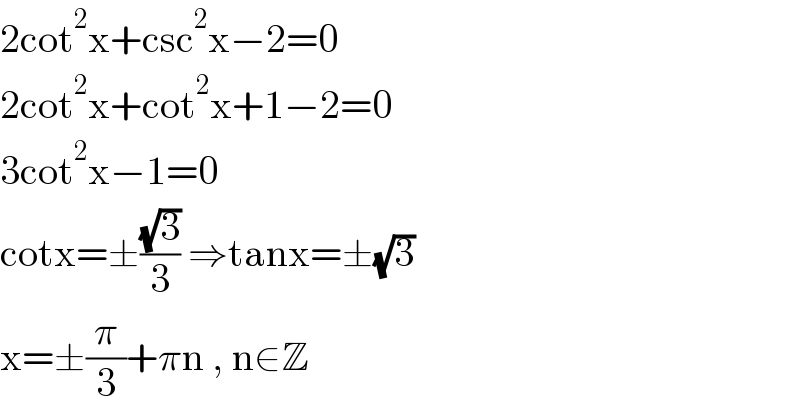
$$\mathrm{2cot}^{\mathrm{2}} \mathrm{x}+\mathrm{csc}^{\mathrm{2}} \mathrm{x}−\mathrm{2}=\mathrm{0} \\ $$$$\mathrm{2cot}^{\mathrm{2}} \mathrm{x}+\mathrm{cot}^{\mathrm{2}} \mathrm{x}+\mathrm{1}−\mathrm{2}=\mathrm{0} \\ $$$$\mathrm{3cot}^{\mathrm{2}} \mathrm{x}−\mathrm{1}=\mathrm{0} \\ $$$$\mathrm{cotx}=\pm\frac{\sqrt{\mathrm{3}}}{\mathrm{3}}\:\Rightarrow\mathrm{tanx}=\pm\sqrt{\mathrm{3}} \\ $$$$\mathrm{x}=\pm\frac{\pi}{\mathrm{3}}+\pi\mathrm{n}\:,\:\mathrm{n}\in\mathbb{Z} \\ $$
