
Question Number 158187 by HongKing last updated on 31/Oct/21
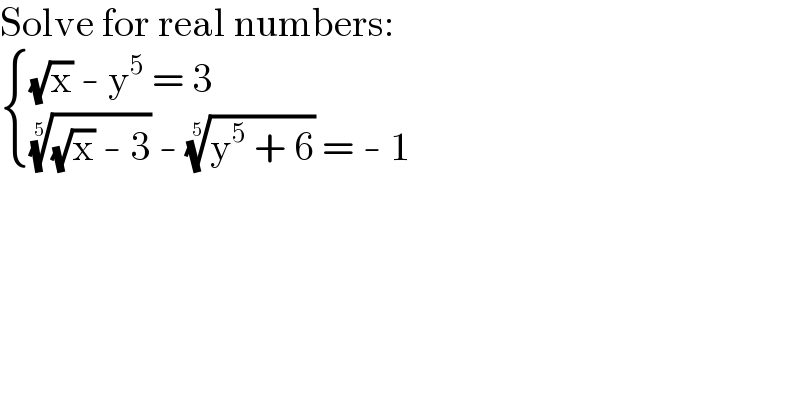
$$\mathrm{Solve}\:\mathrm{for}\:\mathrm{real}\:\mathrm{numbers}: \\ $$$$\begin{cases}{\sqrt{\mathrm{x}}\:-\:\mathrm{y}^{\mathrm{5}} \:=\:\mathrm{3}}\\{\sqrt[{\mathrm{5}}]{\sqrt{\mathrm{x}}\:-\:\mathrm{3}}\:-\:\sqrt[{\mathrm{5}}]{\mathrm{y}^{\mathrm{5}} \:+\:\mathrm{6}}\:=\:-\:\mathrm{1}}\end{cases}\: \\ $$$$ \\ $$
Answered by MJS_new last updated on 31/Oct/21
![(√x)=y^5 +3 [x≥0 ∧ (√x)≥0] y−(y^5 +6)^(1/5) =−1 y^4 +2y^3 +2y^2 +y−1=0 (y^2 +y+((1−(√5))/2))(y^2 +y+((1+(√5))/2))=0 y=((−1+(√(−1+2(√5))))/2) ⇒ x=((7+5(√5))/2)](Q158192.png)
$$\sqrt{{x}}={y}^{\mathrm{5}} +\mathrm{3}\:\left[{x}\geqslant\mathrm{0}\:\wedge\:\sqrt{{x}}\geqslant\mathrm{0}\right] \\ $$$${y}−\left({y}^{\mathrm{5}} +\mathrm{6}\right)^{\mathrm{1}/\mathrm{5}} =−\mathrm{1} \\ $$$${y}^{\mathrm{4}} +\mathrm{2}{y}^{\mathrm{3}} +\mathrm{2}{y}^{\mathrm{2}} +{y}−\mathrm{1}=\mathrm{0} \\ $$$$\left({y}^{\mathrm{2}} +{y}+\frac{\mathrm{1}−\sqrt{\mathrm{5}}}{\mathrm{2}}\right)\left({y}^{\mathrm{2}} +{y}+\frac{\mathrm{1}+\sqrt{\mathrm{5}}}{\mathrm{2}}\right)=\mathrm{0} \\ $$$${y}=\frac{−\mathrm{1}+\sqrt{−\mathrm{1}+\mathrm{2}\sqrt{\mathrm{5}}}}{\mathrm{2}} \\ $$$$\Rightarrow\:{x}=\frac{\mathrm{7}+\mathrm{5}\sqrt{\mathrm{5}}}{\mathrm{2}} \\ $$
Commented by HongKing last updated on 31/Oct/21
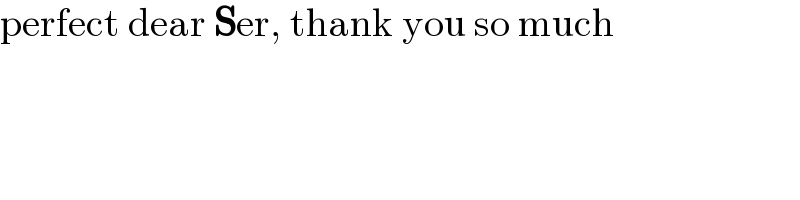
$$\mathrm{perfect}\:\mathrm{dear}\:\boldsymbol{\mathrm{S}}\mathrm{er},\:\mathrm{thank}\:\mathrm{you}\:\mathrm{so}\:\mathrm{much} \\ $$
Commented by ajfour last updated on 01/Nov/21

$${awestrike}\:{precision}! \\ $$
