
Question Number 152892 by mathdanisur last updated on 02/Sep/21

$$\mathrm{Solve}\:\mathrm{for}\:\mathrm{real}\:\mathrm{numbers}\:\mathrm{the}\:\mathrm{following} \\ $$$$\mathrm{system}\:\mathrm{of}\:\mathrm{equations}: \\ $$$$\begin{cases}{\mathrm{x}^{\mathrm{2}} \:-\:\mathrm{yz}\:=\:\mathrm{3}}\\{\mathrm{y}^{\mathrm{2}} \:-\:\mathrm{xz}\:=\:\mathrm{1}}\\{\mathrm{z}^{\mathrm{2}} \:-\:\mathrm{xy}\:=\:-\:\mathrm{1}}\end{cases} \\ $$
Commented by MJS_new last updated on 03/Sep/21
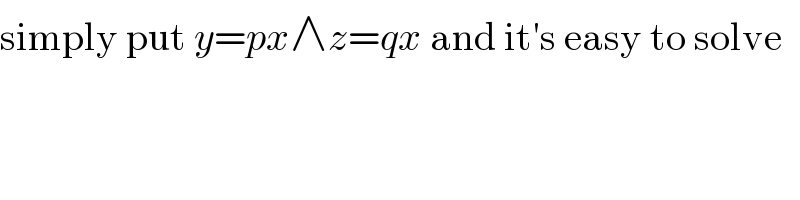
$$\mathrm{simply}\:\mathrm{put}\:{y}={px}\wedge{z}={qx}\:\mathrm{and}\:\mathrm{it}'\mathrm{s}\:\mathrm{easy}\:\mathrm{to}\:\mathrm{solve} \\ $$
Commented by mathdanisur last updated on 03/Sep/21
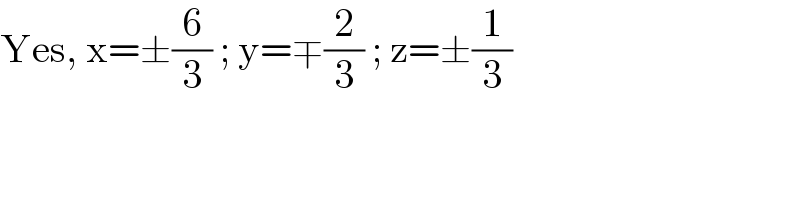
$$\mathrm{Yes},\:\mathrm{x}=\pm\frac{\mathrm{6}}{\mathrm{3}}\:;\:\mathrm{y}=\mp\frac{\mathrm{2}}{\mathrm{3}}\:;\:\mathrm{z}=\pm\frac{\mathrm{1}}{\mathrm{3}} \\ $$
