
Question Number 146854 by mathdanisur last updated on 16/Jul/21
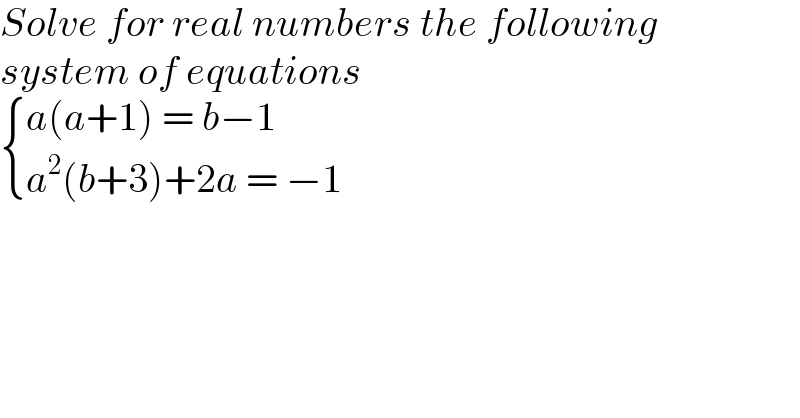
$${Solve}\:{for}\:{real}\:{numbers}\:{the}\:{following} \\ $$$${system}\:{of}\:{equations} \\ $$$$\begin{cases}{{a}\left({a}+\mathrm{1}\right)\:=\:{b}−\mathrm{1}}\\{{a}^{\mathrm{2}} \left({b}+\mathrm{3}\right)+\mathrm{2}{a}\:=\:−\mathrm{1}}\end{cases} \\ $$
Commented by Mrsof last updated on 16/Jul/21
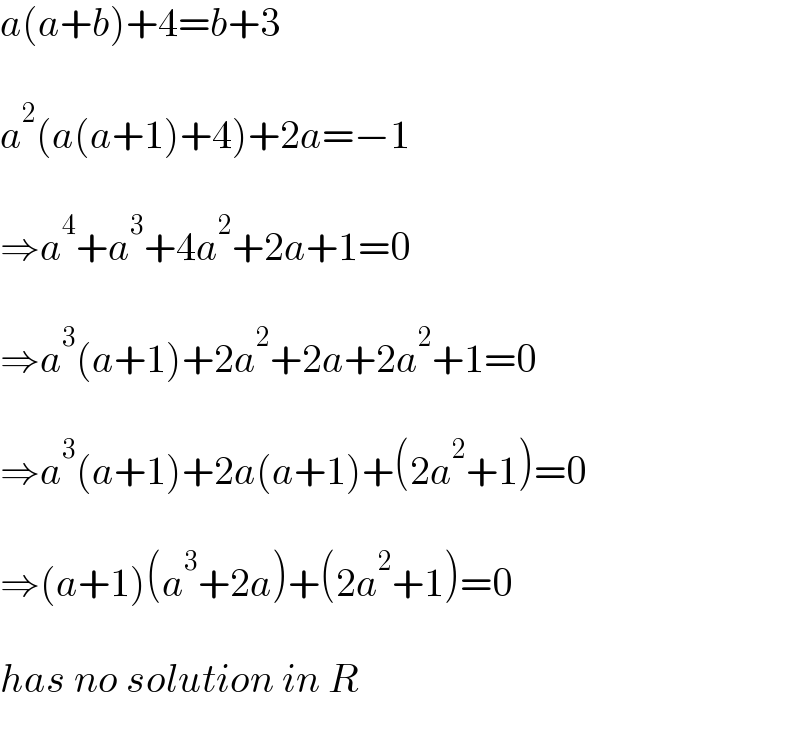
$${a}\left({a}+{b}\right)+\mathrm{4}={b}+\mathrm{3} \\ $$$$ \\ $$$${a}^{\mathrm{2}} \left({a}\left({a}+\mathrm{1}\right)+\mathrm{4}\right)+\mathrm{2}{a}=−\mathrm{1} \\ $$$$ \\ $$$$\Rightarrow{a}^{\mathrm{4}} +{a}^{\mathrm{3}} +\mathrm{4}{a}^{\mathrm{2}} +\mathrm{2}{a}+\mathrm{1}=\mathrm{0} \\ $$$$ \\ $$$$\Rightarrow{a}^{\mathrm{3}} \left({a}+\mathrm{1}\right)+\mathrm{2}{a}^{\mathrm{2}} +\mathrm{2}{a}+\mathrm{2}{a}^{\mathrm{2}} +\mathrm{1}=\mathrm{0} \\ $$$$ \\ $$$$\Rightarrow{a}^{\mathrm{3}} \left({a}+\mathrm{1}\right)+\mathrm{2}{a}\left({a}+\mathrm{1}\right)+\left(\mathrm{2}{a}^{\mathrm{2}} +\mathrm{1}\right)=\mathrm{0} \\ $$$$ \\ $$$$\Rightarrow\left({a}+\mathrm{1}\right)\left({a}^{\mathrm{3}} +\mathrm{2}{a}\right)+\left(\mathrm{2}{a}^{\mathrm{2}} +\mathrm{1}\right)=\mathrm{0} \\ $$$$ \\ $$$${has}\:{no}\:{solution}\:{in}\:{R} \\ $$
Commented by mathdanisur last updated on 16/Jul/21

$${thank}\:{you}\:{Ser} \\ $$
Answered by liberty last updated on 16/Jul/21

$$\:\begin{cases}{{a}\left({a}+\mathrm{1}\right)={b}−\mathrm{1}\Rightarrow{b}={a}^{\mathrm{2}} +{a}+\mathrm{1}}\\{{a}^{\mathrm{2}} \left({b}+\mathrm{3}\right)+\mathrm{2}{a}=−\mathrm{1}}\end{cases} \\ $$$$\:\Rightarrow{a}^{\mathrm{2}} \left({a}^{\mathrm{2}} +{a}+\mathrm{4}\right)+\mathrm{2}{a}+\mathrm{1}=\mathrm{0} \\ $$$$\Rightarrow{a}^{\mathrm{4}} +{a}^{\mathrm{3}} +\mathrm{4}{a}^{\mathrm{2}} +\mathrm{2}{a}+\mathrm{1}=\mathrm{0} \\ $$$$\Rightarrow\left({a}^{\mathrm{2}} +{pa}+\mathrm{1}\right)\left({a}^{\mathrm{2}} +{qa}+\mathrm{1}\right)= \\ $$$$\:\:\:\:\:\:{a}^{\mathrm{4}} +{a}^{\mathrm{3}} +\mathrm{4}{a}^{\mathrm{2}} +\mathrm{2}{a}+\mathrm{1} \\ $$$$\Rightarrow{a}^{\mathrm{4}} +\left({p}+{q}\right){a}^{\mathrm{3}} +\left(\mathrm{2}+{pq}\right){a}^{\mathrm{2}} +\left({p}+{q}\right){a}+\mathrm{1}= \\ $$$$\:\:\:\:{a}^{\mathrm{4}} +{a}^{\mathrm{3}} +\mathrm{4}{a}^{\mathrm{2}} +\mathrm{2}{a}+\mathrm{1} \\ $$$$\Rightarrow\begin{cases}{{p}+{q}=\mathrm{1}}\\{\mathrm{2}+{pq}=\mathrm{4}}\\{{p}+{q}=\mathrm{2}}\end{cases}\:{the}\:{equation}\:{inconsistent} \\ $$
Commented by mathdanisur last updated on 16/Jul/21

$${thank}\:{you}\:{Ser} \\ $$
