
Question Number 157489 by MathSh last updated on 23/Oct/21
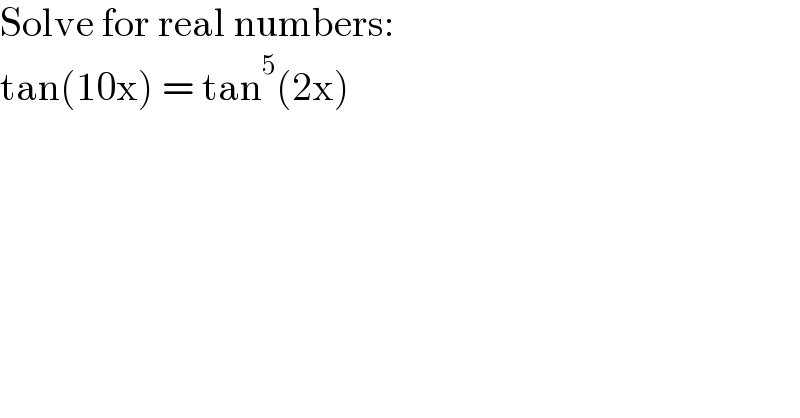
$$\mathrm{Solve}\:\mathrm{for}\:\mathrm{real}\:\mathrm{numbers}: \\ $$$$\mathrm{tan}\left(\mathrm{10x}\right)\:=\:\mathrm{tan}^{\mathrm{5}} \left(\mathrm{2x}\right) \\ $$$$ \\ $$
Answered by MJS_new last updated on 24/Oct/21
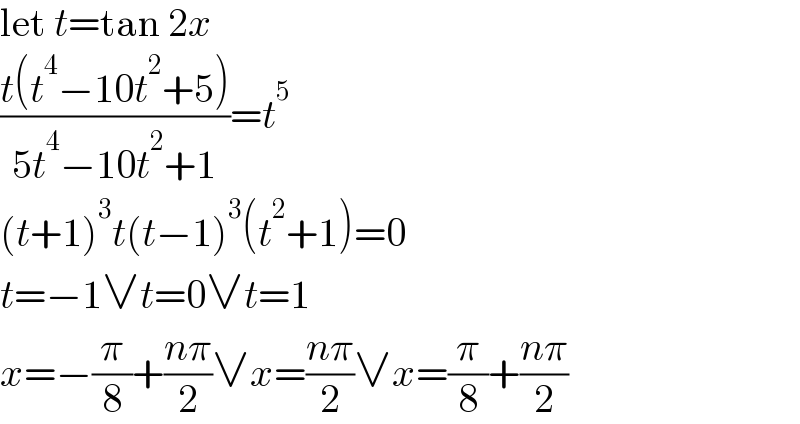
$$\mathrm{let}\:{t}=\mathrm{tan}\:\mathrm{2}{x} \\ $$$$\frac{{t}\left({t}^{\mathrm{4}} −\mathrm{10}{t}^{\mathrm{2}} +\mathrm{5}\right)}{\mathrm{5}{t}^{\mathrm{4}} −\mathrm{10}{t}^{\mathrm{2}} +\mathrm{1}}={t}^{\mathrm{5}} \\ $$$$\left({t}+\mathrm{1}\right)^{\mathrm{3}} {t}\left({t}−\mathrm{1}\right)^{\mathrm{3}} \left({t}^{\mathrm{2}} +\mathrm{1}\right)=\mathrm{0} \\ $$$${t}=−\mathrm{1}\vee{t}=\mathrm{0}\vee{t}=\mathrm{1} \\ $$$${x}=−\frac{\pi}{\mathrm{8}}+\frac{{n}\pi}{\mathrm{2}}\vee{x}=\frac{{n}\pi}{\mathrm{2}}\vee{x}=\frac{\pi}{\mathrm{8}}+\frac{{n}\pi}{\mathrm{2}} \\ $$
Commented by tounghoungko last updated on 24/Oct/21
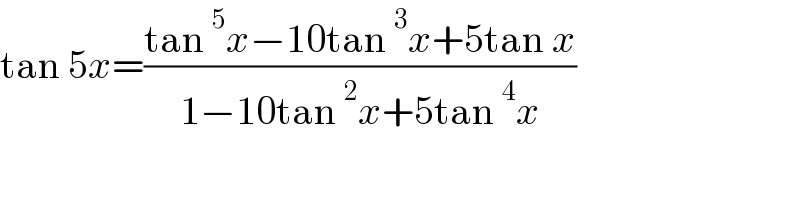
$$\mathrm{tan}\:\mathrm{5}{x}=\frac{\mathrm{tan}\:^{\mathrm{5}} {x}−\mathrm{10tan}\:^{\mathrm{3}} {x}+\mathrm{5tan}\:{x}}{\mathrm{1}−\mathrm{10tan}\:^{\mathrm{2}} {x}+\mathrm{5tan}\:^{\mathrm{4}} {x}} \\ $$
Commented by MJS_new last updated on 24/Oct/21

$$\mathrm{yes} \\ $$
Commented by MathSh last updated on 24/Oct/21
$$\mathrm{Thank}\:\mathrm{you}\:\mathrm{dear}\:\boldsymbol{\mathrm{S}}\mathrm{er}\:\mathrm{very}\:\mathrm{nice} \\ $$
Answered by tounghoungko last updated on 24/Oct/21
![Solve for x∈R . tan (10x)=tan^5 (2x) ⇔ tan (5θ)=((sin^5 θ)/(cos^5 θ)) ,[θ=2x] ⇔((sin 5θ)/(cos 5θ)) = ((sin^5 θ)/(cos^5 θ)) ⇔ ((5sin θ−20sin^3 θ+16sin^5 θ)/(5cos θ−20cos^3 θ+16cos^5 θ))=((sin^5 θ)/(cos^5 θ)) ⇔5sin θcos^5 θ−20sin^3 θcos^5 θ+16sin^5 θcos^5 θ= 5cos θsin^5 θ−20cos^3 θsin^5 θ+16cos^5 θsin^5 θ ⇔sin θcos θ [5cos^4 θ−20sin^2 θcos^4 θ+16sin^4 θcos^4 θ− [5sin^4 θ+20cos^2 θsin^4 θ−16sin^4 θcos^4 θ ]=0 ⇔ (1/2)sin 2θ [5(cos^4 θ−sin^4 θ)+20(cos^2 θsin^4 θ−sin^2 θcos^4 θ)]=0 ⇔(1/2)sin 2θ [5(cos^2 θ−sin^2 θ)+20cos^2 θsin^2 θ(sin^2 θ−cos^2 θ)]=0 ⇔(5/2)sin 2θ cos 2θ (1−sin^2 2θ)=0 ⇔(5/4)sin 4θ (1−sin^2 2θ)=0 (i) (5/4)sin 4θ=0⇒ { ((4θ=2nπ)),((4θ=(1+2n)π)) :} ⇒ { ((8x=2nπ)),((8x=(1+2n)π)) :}⇒ { ((x=((nπ)/4))),((x=(((1+2n)/8))π)) :} (ii) 1−sin^2 2θ=0 ⇒ { ((sin 2θ=1)),((sin 2θ=−1)) :} ⇒ { (( 2θ=(π/2)+2kπ)),((2θ=((3π)/2)+2kπ)) :} { ((4x=(π/2)+2kπ)),((4x=((3π)/2)+2kπ)) :}⇒ { ((x=(((4k+1)/8))π)),((x=(((3+4k)/8))π)) :}](Q157532.png)
$$\:{Solve}\:{for}\:{x}\in{R}\:.\:\mathrm{tan}\:\left(\mathrm{10}{x}\right)=\mathrm{tan}\:^{\mathrm{5}} \left(\mathrm{2}{x}\right) \\ $$$$\Leftrightarrow\:\mathrm{tan}\:\left(\mathrm{5}\theta\right)=\frac{\mathrm{sin}\:^{\mathrm{5}} \theta}{\mathrm{cos}\:^{\mathrm{5}} \theta}\:,\left[\theta=\mathrm{2}{x}\right]\: \\ $$$$\Leftrightarrow\frac{\mathrm{sin}\:\mathrm{5}\theta}{\mathrm{cos}\:\mathrm{5}\theta}\:=\:\frac{\mathrm{sin}\:^{\mathrm{5}} \theta}{\mathrm{cos}\:^{\mathrm{5}} \theta} \\ $$$$\Leftrightarrow\:\frac{\mathrm{5sin}\:\theta−\mathrm{20sin}\:^{\mathrm{3}} \theta+\mathrm{16sin}\:^{\mathrm{5}} \theta}{\mathrm{5cos}\:\theta−\mathrm{20cos}\:^{\mathrm{3}} \theta+\mathrm{16cos}\:^{\mathrm{5}} \theta}=\frac{\mathrm{sin}\:^{\mathrm{5}} \theta}{\mathrm{cos}\:^{\mathrm{5}} \theta} \\ $$$$\Leftrightarrow\mathrm{5sin}\:\theta\mathrm{cos}\:^{\mathrm{5}} \theta−\mathrm{20sin}\:^{\mathrm{3}} \theta\mathrm{cos}\:^{\mathrm{5}} \theta+\mathrm{16sin}\:^{\mathrm{5}} \theta\mathrm{cos}\:^{\mathrm{5}} \theta= \\ $$$$\:\:\:\:\:\mathrm{5cos}\:\theta\mathrm{sin}\:^{\mathrm{5}} \theta−\mathrm{20cos}\:^{\mathrm{3}} \theta\mathrm{sin}\:^{\mathrm{5}} \theta+\mathrm{16cos}\:^{\mathrm{5}} \theta\mathrm{sin}\:^{\mathrm{5}} \theta \\ $$$$\Leftrightarrow\mathrm{sin}\:\theta\mathrm{cos}\:\theta\:\left[\mathrm{5cos}\:^{\mathrm{4}} \theta−\mathrm{20sin}\:^{\mathrm{2}} \theta\mathrm{cos}\:^{\mathrm{4}} \theta+\mathrm{16sin}\:^{\mathrm{4}} \theta\mathrm{cos}\:^{\mathrm{4}} \theta−\right. \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\left[\mathrm{5sin}\:^{\mathrm{4}} \theta+\mathrm{20cos}\:^{\mathrm{2}} \theta\mathrm{sin}\:^{\mathrm{4}} \theta−\mathrm{16sin}\:^{\mathrm{4}} \theta\mathrm{cos}\:^{\mathrm{4}} \theta\:\right]=\mathrm{0} \\ $$$$\Leftrightarrow\:\frac{\mathrm{1}}{\mathrm{2}}\mathrm{sin}\:\mathrm{2}\theta\:\left[\mathrm{5}\left(\mathrm{cos}\:^{\mathrm{4}} \theta−\mathrm{sin}\:^{\mathrm{4}} \theta\right)+\mathrm{20}\left(\mathrm{cos}^{\mathrm{2}} \theta\mathrm{sin}\:^{\mathrm{4}} \theta−\mathrm{sin}\:^{\mathrm{2}} \theta\mathrm{cos}\:^{\mathrm{4}} \theta\right)\right]=\mathrm{0} \\ $$$$\Leftrightarrow\frac{\mathrm{1}}{\mathrm{2}}\mathrm{sin}\:\mathrm{2}\theta\:\left[\mathrm{5}\left(\mathrm{cos}\:^{\mathrm{2}} \theta−\mathrm{sin}\:^{\mathrm{2}} \theta\right)+\mathrm{20cos}\:^{\mathrm{2}} \theta\mathrm{sin}\:^{\mathrm{2}} \theta\left(\mathrm{sin}\:^{\mathrm{2}} \theta−\mathrm{cos}\:^{\mathrm{2}} \theta\right)\right]=\mathrm{0} \\ $$$$\Leftrightarrow\frac{\mathrm{5}}{\mathrm{2}}\mathrm{sin}\:\mathrm{2}\theta\:\mathrm{cos}\:\mathrm{2}\theta\:\left(\mathrm{1}−\mathrm{sin}\:^{\mathrm{2}} \mathrm{2}\theta\right)=\mathrm{0} \\ $$$$\Leftrightarrow\frac{\mathrm{5}}{\mathrm{4}}\mathrm{sin}\:\mathrm{4}\theta\:\left(\mathrm{1}−\mathrm{sin}\:^{\mathrm{2}} \mathrm{2}\theta\right)=\mathrm{0} \\ $$$$\left({i}\right)\:\frac{\mathrm{5}}{\mathrm{4}}\mathrm{sin}\:\mathrm{4}\theta=\mathrm{0}\Rightarrow\:\begin{cases}{\mathrm{4}\theta=\mathrm{2}{n}\pi}\\{\mathrm{4}\theta=\left(\mathrm{1}+\mathrm{2}{n}\right)\pi}\end{cases}\: \\ $$$$\Rightarrow\:\begin{cases}{\mathrm{8}{x}=\mathrm{2}{n}\pi}\\{\mathrm{8}{x}=\left(\mathrm{1}+\mathrm{2}{n}\right)\pi}\end{cases}\Rightarrow\begin{cases}{{x}=\frac{{n}\pi}{\mathrm{4}}}\\{{x}=\left(\frac{\mathrm{1}+\mathrm{2}{n}}{\mathrm{8}}\right)\pi}\end{cases} \\ $$$$\left({ii}\right)\:\mathrm{1}−\mathrm{sin}\:^{\mathrm{2}} \mathrm{2}\theta=\mathrm{0} \\ $$$$\Rightarrow\begin{cases}{\mathrm{sin}\:\mathrm{2}\theta=\mathrm{1}}\\{\mathrm{sin}\:\mathrm{2}\theta=−\mathrm{1}}\end{cases}\:\Rightarrow\begin{cases}{\:\mathrm{2}\theta=\frac{\pi}{\mathrm{2}}+\mathrm{2}{k}\pi}\\{\mathrm{2}\theta=\frac{\mathrm{3}\pi}{\mathrm{2}}+\mathrm{2}{k}\pi}\end{cases} \\ $$$$\:\begin{cases}{\mathrm{4}{x}=\frac{\pi}{\mathrm{2}}+\mathrm{2}{k}\pi}\\{\mathrm{4}{x}=\frac{\mathrm{3}\pi}{\mathrm{2}}+\mathrm{2}{k}\pi}\end{cases}\Rightarrow\begin{cases}{{x}=\left(\frac{\mathrm{4}{k}+\mathrm{1}}{\mathrm{8}}\right)\pi}\\{{x}=\left(\frac{\mathrm{3}+\mathrm{4}{k}}{\mathrm{8}}\right)\pi}\end{cases} \\ $$
Commented by MathSh last updated on 24/Oct/21
$$\mathrm{Thank}\:\mathrm{you}\:\mathrm{dear}\:\boldsymbol{\mathrm{S}}\mathrm{er}\:\mathrm{cool} \\ $$
