
Question Number 157265 by MathSh last updated on 21/Oct/21
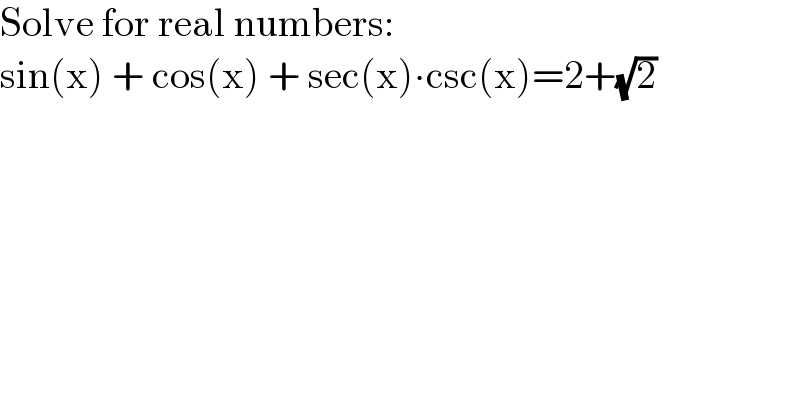
$$\mathrm{Solve}\:\mathrm{for}\:\mathrm{real}\:\mathrm{numbers}: \\ $$$$\mathrm{sin}\left(\mathrm{x}\right)\:+\:\mathrm{cos}\left(\mathrm{x}\right)\:+\:\mathrm{sec}\left(\mathrm{x}\right)\centerdot\mathrm{csc}\left(\mathrm{x}\right)=\mathrm{2}+\sqrt{\mathrm{2}} \\ $$
Answered by TheSupreme last updated on 21/Oct/21
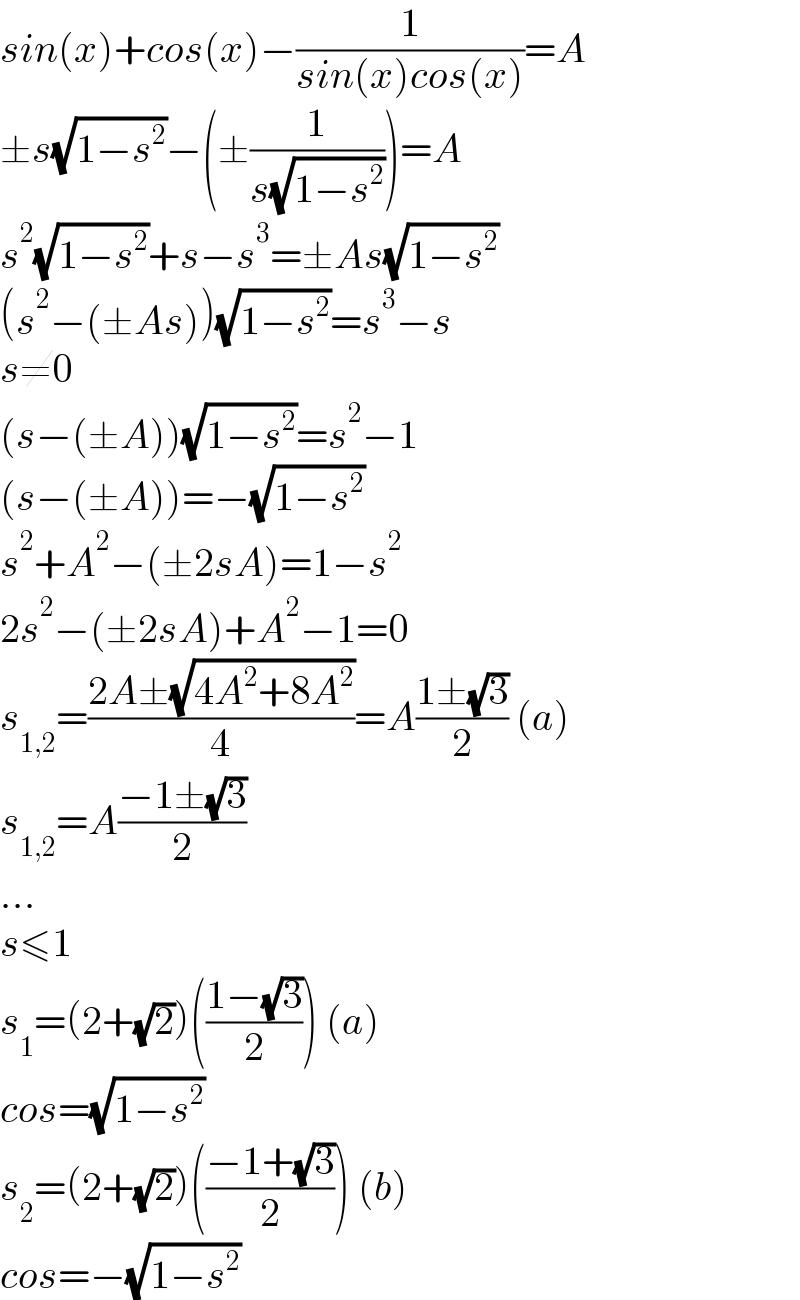
$${sin}\left({x}\right)+{cos}\left({x}\right)−\frac{\mathrm{1}}{{sin}\left({x}\right){cos}\left({x}\right)}={A} \\ $$$$\pm{s}\sqrt{\mathrm{1}−{s}^{\mathrm{2}} }−\left(\pm\frac{\mathrm{1}}{{s}\sqrt{\mathrm{1}−{s}^{\mathrm{2}} }}\right)={A} \\ $$$${s}^{\mathrm{2}} \sqrt{\mathrm{1}−{s}^{\mathrm{2}} }+{s}−{s}^{\mathrm{3}} =\pm{As}\sqrt{\mathrm{1}−{s}^{\mathrm{2}} } \\ $$$$\left({s}^{\mathrm{2}} −\left(\pm{As}\right)\right)\sqrt{\mathrm{1}−{s}^{\mathrm{2}} }={s}^{\mathrm{3}} −{s} \\ $$$${s}\neq\mathrm{0} \\ $$$$\left({s}−\left(\pm{A}\right)\right)\sqrt{\mathrm{1}−{s}^{\mathrm{2}} }={s}^{\mathrm{2}} −\mathrm{1} \\ $$$$\left({s}−\left(\pm{A}\right)\right)=−\sqrt{\mathrm{1}−{s}^{\mathrm{2}} } \\ $$$${s}^{\mathrm{2}} +{A}^{\mathrm{2}} −\left(\pm\mathrm{2}{sA}\right)=\mathrm{1}−{s}^{\mathrm{2}} \\ $$$$\mathrm{2}{s}^{\mathrm{2}} −\left(\pm\mathrm{2}{sA}\right)+{A}^{\mathrm{2}} −\mathrm{1}=\mathrm{0} \\ $$$${s}_{\mathrm{1},\mathrm{2}} =\frac{\mathrm{2}{A}\pm\sqrt{\mathrm{4}{A}^{\mathrm{2}} +\mathrm{8}{A}^{\mathrm{2}} }}{\mathrm{4}}={A}\frac{\mathrm{1}\pm\sqrt{\mathrm{3}}}{\mathrm{2}}\:\left({a}\right) \\ $$$${s}_{\mathrm{1},\mathrm{2}} ={A}\frac{−\mathrm{1}\pm\sqrt{\mathrm{3}}}{\mathrm{2}} \\ $$$$...\: \\ $$$${s}\leqslant\mathrm{1} \\ $$$${s}_{\mathrm{1}} =\left(\mathrm{2}+\sqrt{\mathrm{2}}\right)\left(\frac{\mathrm{1}−\sqrt{\mathrm{3}}}{\mathrm{2}}\right)\:\left({a}\right) \\ $$$${cos}=\sqrt{\mathrm{1}−{s}^{\mathrm{2}} } \\ $$$${s}_{\mathrm{2}} =\left(\mathrm{2}+\sqrt{\mathrm{2}}\right)\left(\frac{−\mathrm{1}+\sqrt{\mathrm{3}}}{\mathrm{2}}\right)\:\left({b}\right) \\ $$$${cos}=−\sqrt{\mathrm{1}−{s}^{\mathrm{2}} } \\ $$
