
Question Number 138725 by mathsuji last updated on 17/Apr/21
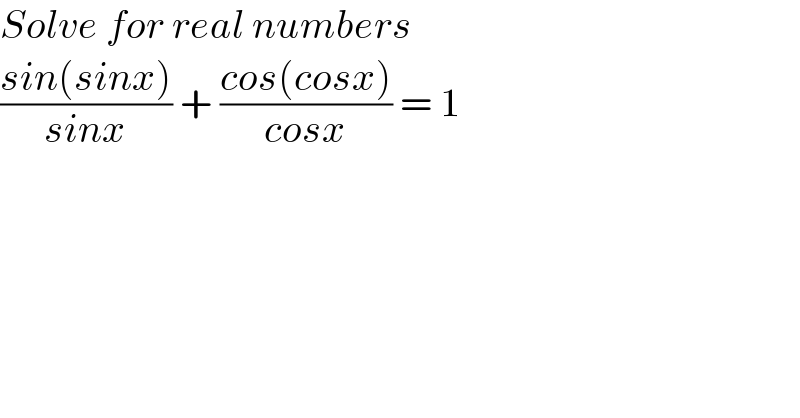
$${Solve}\:{for}\:{real}\:{numbers} \\ $$$$\frac{{sin}\left({sinx}\right)}{{sinx}}\:+\:\frac{{cos}\left({cosx}\right)}{{cosx}}\:=\:\mathrm{1} \\ $$
Answered by mr W last updated on 18/Apr/21

$${t}=\mathrm{sin}\:{x} \\ $$$$\mathrm{cos}\:{x}=\pm\sqrt{\mathrm{1}−{t}^{\mathrm{2}} } \\ $$$$−\mathrm{1}\leqslant{t}\leqslant\mathrm{1} \\ $$$${f}\left({t}\right)=\frac{\mathrm{sin}\:{t}}{{t}}+\frac{\mathrm{cos}\:\sqrt{\mathrm{1}−{t}^{\mathrm{2}} }}{\:\sqrt{\mathrm{1}−{t}^{\mathrm{2}} }}\geqslant{f}\left(\mathrm{0}\right)=\mathrm{1}+\mathrm{cos}\:\mathrm{1}>\mathrm{1} \\ $$$$\Rightarrow{no}\:{solution}\:{for}\:{f}\left({t}\right)=\mathrm{1} \\ $$$${g}\left({t}\right)=\frac{\mathrm{sin}\:{t}}{{t}}−\frac{\mathrm{cos}\:\sqrt{\mathrm{1}−{t}^{\mathrm{2}} }}{\:\sqrt{\mathrm{1}−{t}^{\mathrm{2}} }}\leqslant{g}\left(\mathrm{0}\right)=\mathrm{1}−\mathrm{cos}\:\mathrm{1}<\mathrm{1}= \\ $$$$\Rightarrow{no}\:{solution}\:{for}\:{g}\left({t}\right)=\mathrm{1} \\ $$$$ \\ $$$$\Rightarrow{no}\:{solution}\:{for} \\ $$$$\frac{{sin}\left({sinx}\right)}{{sinx}}\:+\:\frac{{cos}\left({cosx}\right)}{{cosx}}\:=\:\mathrm{1}! \\ $$$$ \\ $$$$\frac{{sin}\left({sinx}\right)}{{sinx}}\:+\:\frac{{cos}\left({cosx}\right)}{{cosx}}\:=\:{a}\:{has}\:{roots} \\ $$$${only}\:{if}\:{a}\geqslant\mathrm{1}+\mathrm{cos}\:\mathrm{1}\:{or}\:{a}\leqslant\mathrm{1}−\mathrm{cos}\:\mathrm{1} \\ $$
Commented by mathsuji last updated on 20/Apr/21

$${THANKS}\:{SIR} \\ $$
