Question and Answers Forum

All Questions      Topic List

Algebra Questions

Previous in All Question      Next in All Question      

Previous in Algebra      Next in Algebra      

Question Number 139577 by bemath last updated on 29/Apr/21

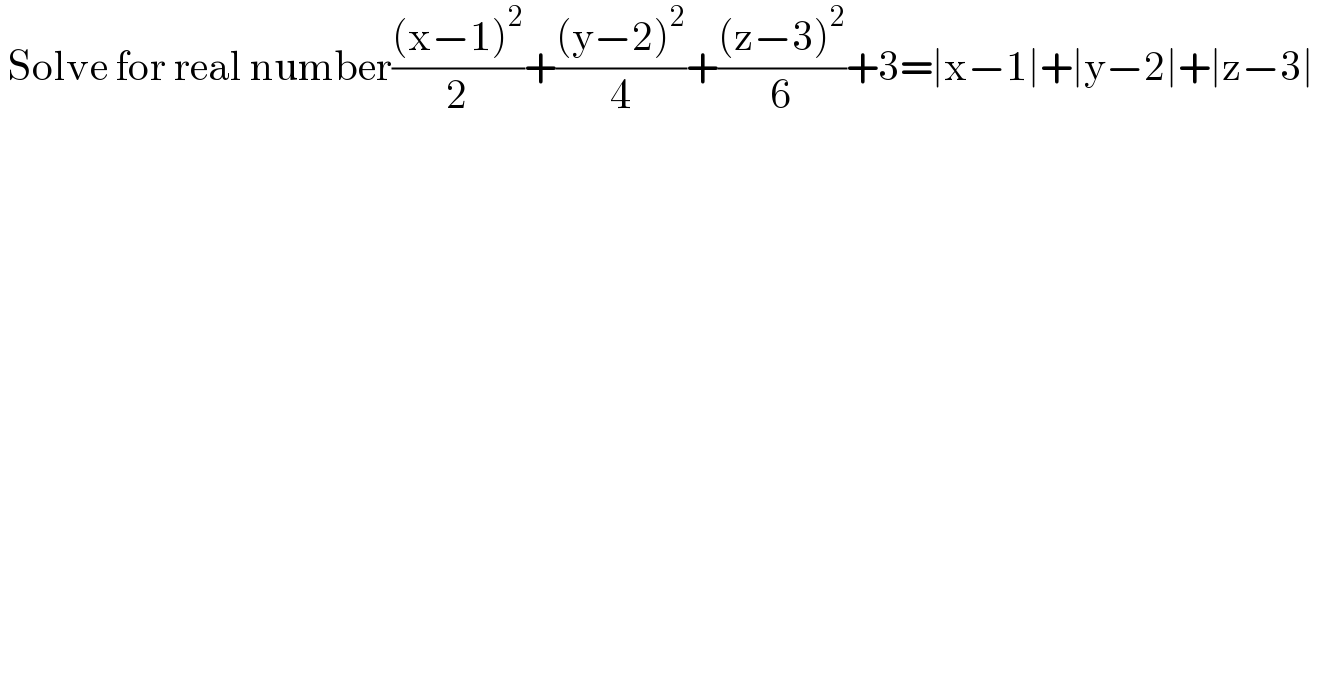
Solve for real number(((x−1)^2 )/2)+(((y−2)^2 )/4)+(((z−3)^2 )/6)+3=∣x−1∣+∣y−2∣+∣z−3∣

$$\:\mathrm{Solve}\:\mathrm{for}\:\mathrm{real}\:\mathrm{number}\frac{\left(\mathrm{x}−\mathrm{1}\right)^{\mathrm{2}} }{\mathrm{2}}+\frac{\left(\mathrm{y}−\mathrm{2}\right)^{\mathrm{2}} }{\mathrm{4}}+\frac{\left(\mathrm{z}−\mathrm{3}\right)^{\mathrm{2}} }{\mathrm{6}}+\mathrm{3}=\mid\mathrm{x}−\mathrm{1}\mid+\mid\mathrm{y}−\mathrm{2}\mid+\mid\mathrm{z}−\mathrm{3}\mid\: \\ $$

Answered by mr W last updated on 29/Apr/21

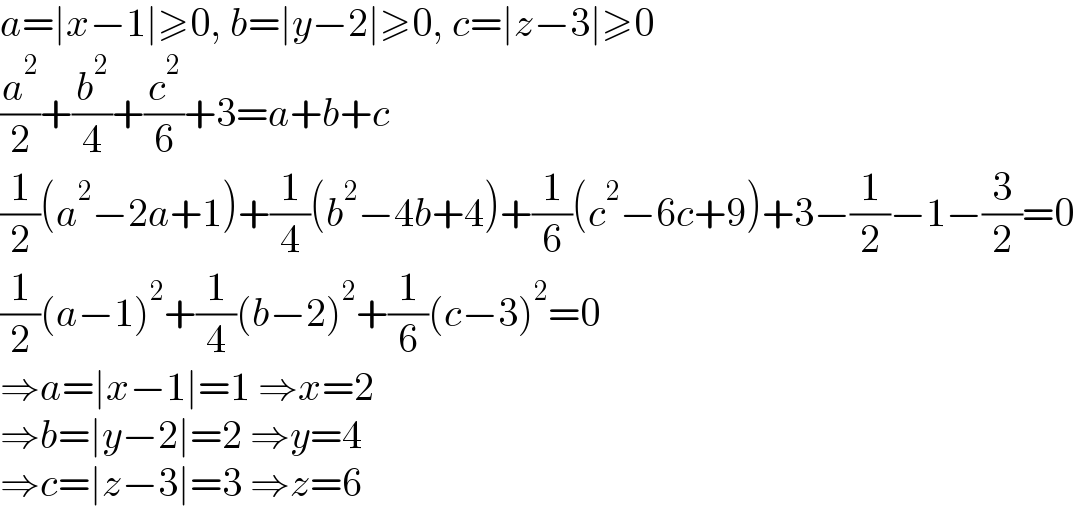
a=∣x−1∣≥0, b=∣y−2∣≥0, c=∣z−3∣≥0 (a^2 /2)+(b^2 /4)+(c^2 /6)+3=a+b+c (1/2)(a^2 −2a+1)+(1/4)(b^2 −4b+4)+(1/6)(c^2 −6c+9)+3−(1/2)−1−(3/2)=0 (1/2)(a−1)^2 +(1/4)(b−2)^2 +(1/6)(c−3)^2 =0 ⇒a=∣x−1∣=1 ⇒x=2 ⇒b=∣y−2∣=2 ⇒y=4 ⇒c=∣z−3∣=3 ⇒z=6

$${a}=\mid{x}−\mathrm{1}\mid\geqslant\mathrm{0},\:{b}=\mid{y}−\mathrm{2}\mid\geqslant\mathrm{0},\:{c}=\mid{z}−\mathrm{3}\mid\geqslant\mathrm{0} \\ $$$$\frac{{a}^{\mathrm{2}} }{\mathrm{2}}+\frac{{b}^{\mathrm{2}} }{\mathrm{4}}+\frac{{c}^{\mathrm{2}} }{\mathrm{6}}+\mathrm{3}={a}+{b}+{c} \\ $$$$\frac{\mathrm{1}}{\mathrm{2}}\left({a}^{\mathrm{2}} −\mathrm{2}{a}+\mathrm{1}\right)+\frac{\mathrm{1}}{\mathrm{4}}\left({b}^{\mathrm{2}} −\mathrm{4}{b}+\mathrm{4}\right)+\frac{\mathrm{1}}{\mathrm{6}}\left({c}^{\mathrm{2}} −\mathrm{6}{c}+\mathrm{9}\right)+\mathrm{3}−\frac{\mathrm{1}}{\mathrm{2}}−\mathrm{1}−\frac{\mathrm{3}}{\mathrm{2}}=\mathrm{0} \\ $$$$\frac{\mathrm{1}}{\mathrm{2}}\left({a}−\mathrm{1}\right)^{\mathrm{2}} +\frac{\mathrm{1}}{\mathrm{4}}\left({b}−\mathrm{2}\right)^{\mathrm{2}} +\frac{\mathrm{1}}{\mathrm{6}}\left({c}−\mathrm{3}\right)^{\mathrm{2}} =\mathrm{0} \\ $$$$\Rightarrow{a}=\mid{x}−\mathrm{1}\mid=\mathrm{1}\:\Rightarrow{x}=\mathrm{2} \\ $$$$\Rightarrow{b}=\mid{y}−\mathrm{2}\mid=\mathrm{2}\:\Rightarrow{y}=\mathrm{4} \\ $$$$\Rightarrow{c}=\mid{z}−\mathrm{3}\mid=\mathrm{3}\:\Rightarrow{z}=\mathrm{6} \\ $$

Commented by Rasheed.Sindhi last updated on 29/Apr/21

V Nice as usual!

$$\mathcal{V}\:\mathcal{N}{ice}\:{as}\:{usual}! \\ $$

Commented by mr W last updated on 29/Apr/21

thanks sir!

$${thanks}\:{sir}! \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com