Question and Answers Forum

All Questions      Topic List

Algebra Questions

Previous in All Question      Next in All Question      

Previous in Algebra      Next in Algebra      

Question Number 155344 by mathdanisur last updated on 29/Sep/21

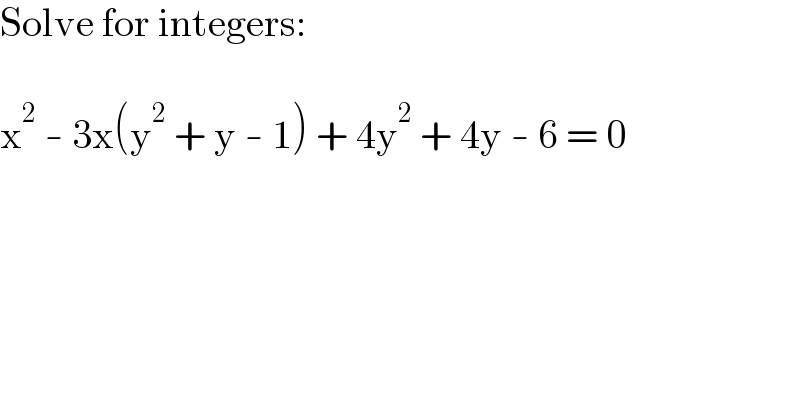
Solve for integers: x^2 - 3x(y^2 + y - 1) + 4y^2 + 4y - 6 = 0

$$\mathrm{Solve}\:\mathrm{for}\:\mathrm{integers}: \\ $$$$ \\ $$$$\mathrm{x}^{\mathrm{2}} \:-\:\mathrm{3x}\left(\mathrm{y}^{\mathrm{2}} \:+\:\mathrm{y}\:-\:\mathrm{1}\right)\:+\:\mathrm{4y}^{\mathrm{2}} \:+\:\mathrm{4y}\:-\:\mathrm{6}\:=\:\mathrm{0} \\ $$

Answered by ghimisi last updated on 29/Sep/21

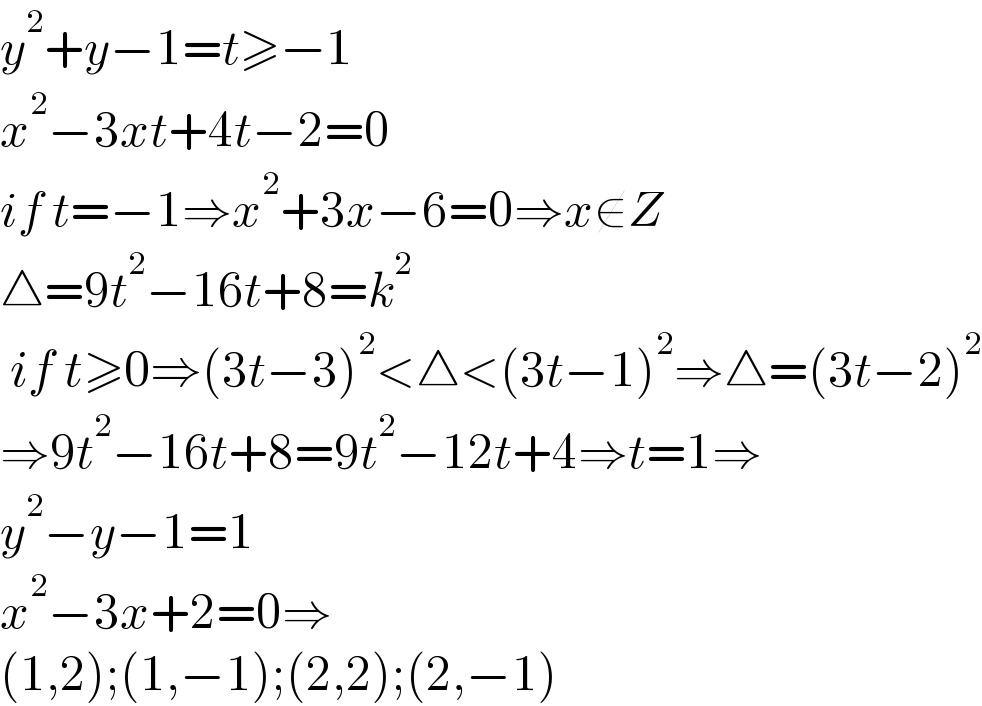
y^2 +y−1=t≥−1 x^2 −3xt+4t−2=0 if t=−1⇒x^2 +3x−6=0⇒x∉Z △=9t^2 −16t+8=k^2 if t≥0⇒(3t−3)^2 <△<(3t−1)^2 ⇒△=(3t−2)^2 ⇒9t^2 −16t+8=9t^2 −12t+4⇒t=1⇒ y^2 −y−1=1 x^2 −3x+2=0⇒ (1,2);(1,−1);(2,2);(2,−1)

$${y}^{\mathrm{2}} +{y}−\mathrm{1}={t}\geqslant−\mathrm{1} \\ $$$${x}^{\mathrm{2}} −\mathrm{3}{xt}+\mathrm{4}{t}−\mathrm{2}=\mathrm{0} \\ $$$${if}\:{t}=−\mathrm{1}\Rightarrow{x}^{\mathrm{2}} +\mathrm{3}{x}−\mathrm{6}=\mathrm{0}\Rightarrow{x}\notin{Z} \\ $$$$\bigtriangleup=\mathrm{9}{t}^{\mathrm{2}} −\mathrm{16}{t}+\mathrm{8}={k}^{\mathrm{2}} \\ $$$$\:{if}\:{t}\geqslant\mathrm{0}\Rightarrow\left(\mathrm{3}{t}−\mathrm{3}\right)^{\mathrm{2}} <\bigtriangleup<\left(\mathrm{3}{t}−\mathrm{1}\right)^{\mathrm{2}} \Rightarrow\bigtriangleup=\left(\mathrm{3}{t}−\mathrm{2}\right)^{\mathrm{2}} \\ $$$$\Rightarrow\mathrm{9}{t}^{\mathrm{2}} −\mathrm{16}{t}+\mathrm{8}=\mathrm{9}{t}^{\mathrm{2}} −\mathrm{12}{t}+\mathrm{4}\Rightarrow{t}=\mathrm{1}\Rightarrow \\ $$$${y}^{\mathrm{2}} −{y}−\mathrm{1}=\mathrm{1} \\ $$$${x}^{\mathrm{2}} −\mathrm{3}{x}+\mathrm{2}=\mathrm{0}\Rightarrow \\ $$$$\left(\mathrm{1},\mathrm{2}\right);\left(\mathrm{1},−\mathrm{1}\right);\left(\mathrm{2},\mathrm{2}\right);\left(\mathrm{2},−\mathrm{1}\right) \\ $$

Commented by mathdanisur last updated on 29/Sep/21

Very nice solution Ser thankyou

$$\mathrm{Very}\:\mathrm{nice}\:\mathrm{solution}\:\boldsymbol{\mathrm{S}}\mathrm{er}\:\mathrm{thankyou} \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com