
Question Number 158274 by HongKing last updated on 01/Nov/21
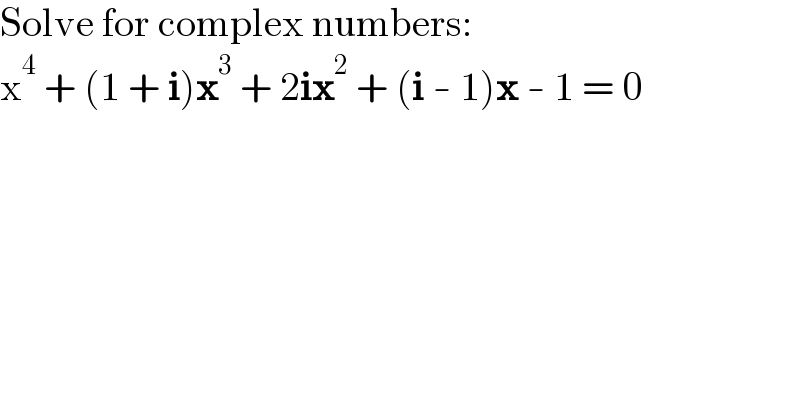
$$\mathrm{Solve}\:\mathrm{for}\:\mathrm{complex}\:\mathrm{numbers}: \\ $$$$\mathrm{x}^{\mathrm{4}} \:+\:\left(\mathrm{1}\:+\:\boldsymbol{\mathrm{i}}\right)\boldsymbol{\mathrm{x}}^{\mathrm{3}} \:+\:\mathrm{2}\boldsymbol{\mathrm{ix}}^{\mathrm{2}} \:+\:\left(\boldsymbol{\mathrm{i}}\:-\:\mathrm{1}\right)\boldsymbol{\mathrm{x}}\:-\:\mathrm{1}\:=\:\mathrm{0} \\ $$$$ \\ $$
Answered by mindispower last updated on 01/Nov/21
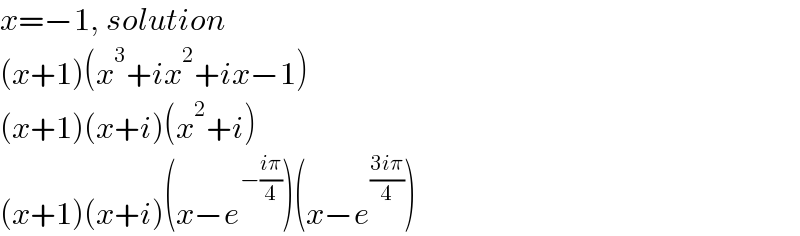
$${x}=−\mathrm{1},\:{solution}\: \\ $$$$\left({x}+\mathrm{1}\right)\left({x}^{\mathrm{3}} +{ix}^{\mathrm{2}} +{ix}−\mathrm{1}\right) \\ $$$$\left({x}+\mathrm{1}\right)\left({x}+{i}\right)\left({x}^{\mathrm{2}} +{i}\right) \\ $$$$\left({x}+\mathrm{1}\right)\left({x}+{i}\right)\left({x}−{e}^{−\frac{{i}\pi}{\mathrm{4}}} \right)\left({x}−{e}^{\frac{\mathrm{3}{i}\pi}{\mathrm{4}}} \right) \\ $$
