
Question Number 183038 by Mastermind last updated on 18/Dec/22

$$\mathrm{Solve} \\ $$$$\frac{\mathrm{dy}}{\mathrm{dx}}+\mathrm{xy}=\mathrm{x}^{\mathrm{2}} \\ $$$$ \\ $$$$\mathrm{M}.\mathrm{m} \\ $$
Answered by TheSupreme last updated on 21/Dec/22
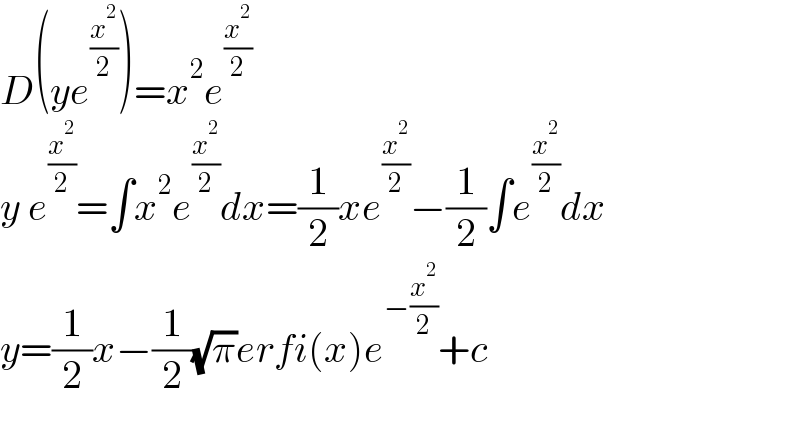
$${D}\left({ye}^{\frac{{x}^{\mathrm{2}} }{\mathrm{2}}} \right)={x}^{\mathrm{2}} {e}^{\frac{{x}^{\mathrm{2}} }{\mathrm{2}}} \\ $$$${y}\:{e}^{\frac{{x}^{\mathrm{2}} }{\mathrm{2}}} =\int{x}^{\mathrm{2}} {e}^{\frac{{x}^{\mathrm{2}} }{\mathrm{2}}} {dx}=\frac{\mathrm{1}}{\mathrm{2}}{xe}^{\frac{{x}^{\mathrm{2}} }{\mathrm{2}}} −\frac{\mathrm{1}}{\mathrm{2}}\int{e}^{\frac{{x}^{\mathrm{2}} }{\mathrm{2}}} {dx} \\ $$$${y}=\frac{\mathrm{1}}{\mathrm{2}}{x}−\frac{\mathrm{1}}{\mathrm{2}}\sqrt{\pi}{erfi}\left({x}\right){e}^{−\frac{{x}^{\mathrm{2}} }{\mathrm{2}}} +{c} \\ $$$$ \\ $$
