
Question Number 42012 by rahul 19 last updated on 16/Aug/18

$$\mathrm{Solve}\:: \\ $$$$\frac{{d}\mathrm{u}}{{d}\mathrm{t}}\:=\:\frac{\mathrm{3u}−\mathrm{7t}}{−\mathrm{7u}+\mathrm{3t}} \\ $$
Answered by tanmay.chaudhury50@gmail.com last updated on 16/Aug/18
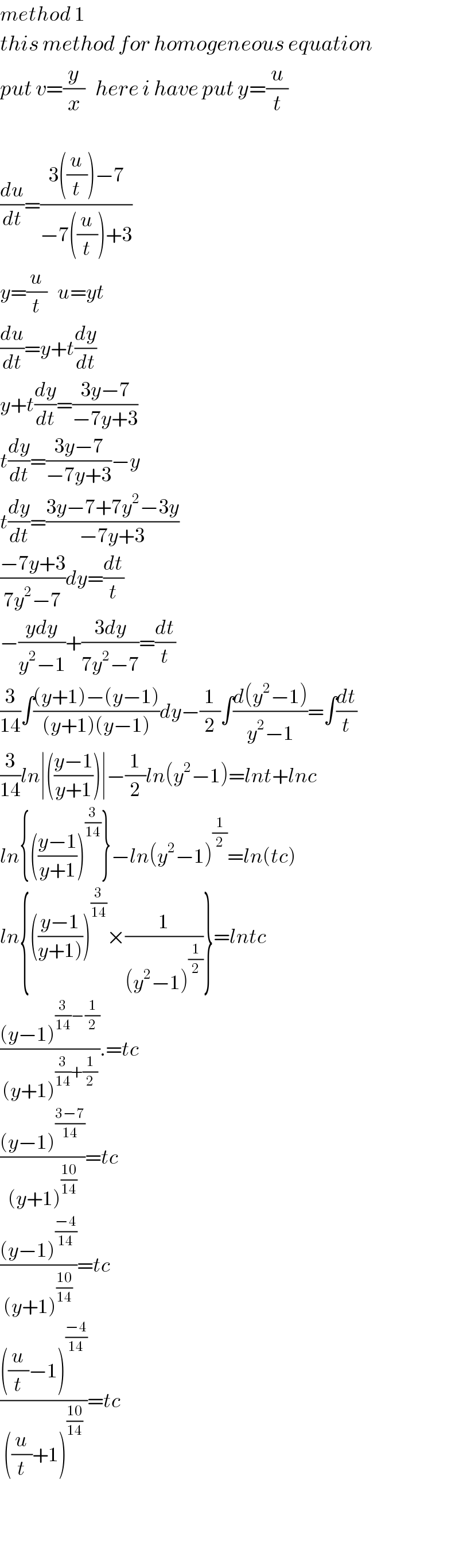
$${method}\:\mathrm{1} \\ $$$${this}\:{method}\:{for}\:{homogeneous}\:{equation} \\ $$$${put}\:{v}=\frac{{y}}{{x}}\:\:\:{here}\:{i}\:{have}\:{put}\:{y}=\frac{{u}}{{t}} \\ $$$$ \\ $$$$\frac{{du}}{{dt}}=\frac{\mathrm{3}\left(\frac{{u}}{{t}}\right)−\mathrm{7}}{−\mathrm{7}\left(\frac{{u}}{{t}}\right)+\mathrm{3}} \\ $$$${y}=\frac{{u}}{{t}}\:\:\:{u}={yt} \\ $$$$\frac{{du}}{{dt}}={y}+{t}\frac{{dy}}{{dt}} \\ $$$${y}+{t}\frac{{dy}}{{dt}}=\frac{\mathrm{3}{y}−\mathrm{7}}{−\mathrm{7}{y}+\mathrm{3}} \\ $$$${t}\frac{{dy}}{{dt}}=\frac{\mathrm{3}{y}−\mathrm{7}}{−\mathrm{7}{y}+\mathrm{3}}−{y} \\ $$$${t}\frac{{dy}}{{dt}}=\frac{\mathrm{3}{y}−\mathrm{7}+\mathrm{7}{y}^{\mathrm{2}} −\mathrm{3}{y}}{−\mathrm{7}{y}+\mathrm{3}} \\ $$$$\frac{−\mathrm{7}{y}+\mathrm{3}}{\mathrm{7}{y}^{\mathrm{2}} −\mathrm{7}}{dy}=\frac{{dt}}{{t}} \\ $$$$−\frac{{ydy}}{{y}^{\mathrm{2}} −\mathrm{1}}+\frac{\mathrm{3}{dy}}{\mathrm{7}{y}^{\mathrm{2}} −\mathrm{7}}=\frac{{dt}}{{t}} \\ $$$$\frac{\mathrm{3}}{\mathrm{14}}\int\frac{\left({y}+\mathrm{1}\right)−\left({y}−\mathrm{1}\right)}{\left({y}+\mathrm{1}\right)\left({y}−\mathrm{1}\right)}{dy}−\frac{\mathrm{1}}{\mathrm{2}}\int\frac{{d}\left({y}^{\mathrm{2}} −\mathrm{1}\right)}{{y}^{\mathrm{2}} −\mathrm{1}}=\int\frac{{dt}}{{t}} \\ $$$$\frac{\mathrm{3}}{\mathrm{14}}{ln}\mid\left(\frac{{y}−\mathrm{1}}{{y}+\mathrm{1}}\right)\mid−\frac{\mathrm{1}}{\mathrm{2}}{ln}\left({y}^{\mathrm{2}} −\mathrm{1}\right)={lnt}+{lnc} \\ $$$${ln}\left\{\left(\frac{{y}−\mathrm{1}}{{y}+\mathrm{1}}\right)^{\frac{\mathrm{3}}{\mathrm{14}}} \right\}−{ln}\left({y}^{\mathrm{2}} −\mathrm{1}\right)^{\frac{\mathrm{1}}{\mathrm{2}}} ={ln}\left({tc}\right) \\ $$$${ln}\left\{\left(\frac{{y}−\mathrm{1}}{\left.{y}+\mathrm{1}\right)}\right)^{\frac{\mathrm{3}}{\mathrm{14}}} ×\frac{\mathrm{1}}{\left({y}^{\mathrm{2}} −\mathrm{1}\right)^{\frac{\mathrm{1}}{\mathrm{2}}} }\right\}={lntc} \\ $$$$\frac{\left({y}−\mathrm{1}\right)^{\frac{\mathrm{3}}{\mathrm{14}}−\frac{\mathrm{1}}{\mathrm{2}}} }{\left({y}+\mathrm{1}\right)^{\frac{\mathrm{3}}{\mathrm{14}}+\frac{\mathrm{1}}{\mathrm{2}}} }.={tc} \\ $$$$\frac{\left({y}−\mathrm{1}\right)^{\frac{\mathrm{3}−\mathrm{7}}{\mathrm{14}}} }{\left({y}+\mathrm{1}\right)^{\frac{\mathrm{10}}{\mathrm{14}}} }={tc} \\ $$$$\frac{\left({y}−\mathrm{1}\right)^{\frac{−\mathrm{4}}{\mathrm{14}}} }{\left({y}+\mathrm{1}\right)^{\frac{\mathrm{10}}{\mathrm{14}}} }={tc} \\ $$$$\frac{\left(\frac{{u}}{{t}}−\mathrm{1}\right)^{\frac{−\mathrm{4}}{\mathrm{14}}} }{\left(\frac{{u}}{{t}}+\mathrm{1}\right)^{\frac{\mathrm{10}}{\mathrm{14}}} }={tc} \\ $$$$ \\ $$$$ \\ $$
Answered by tanmay.chaudhury50@gmail.com last updated on 16/Aug/18
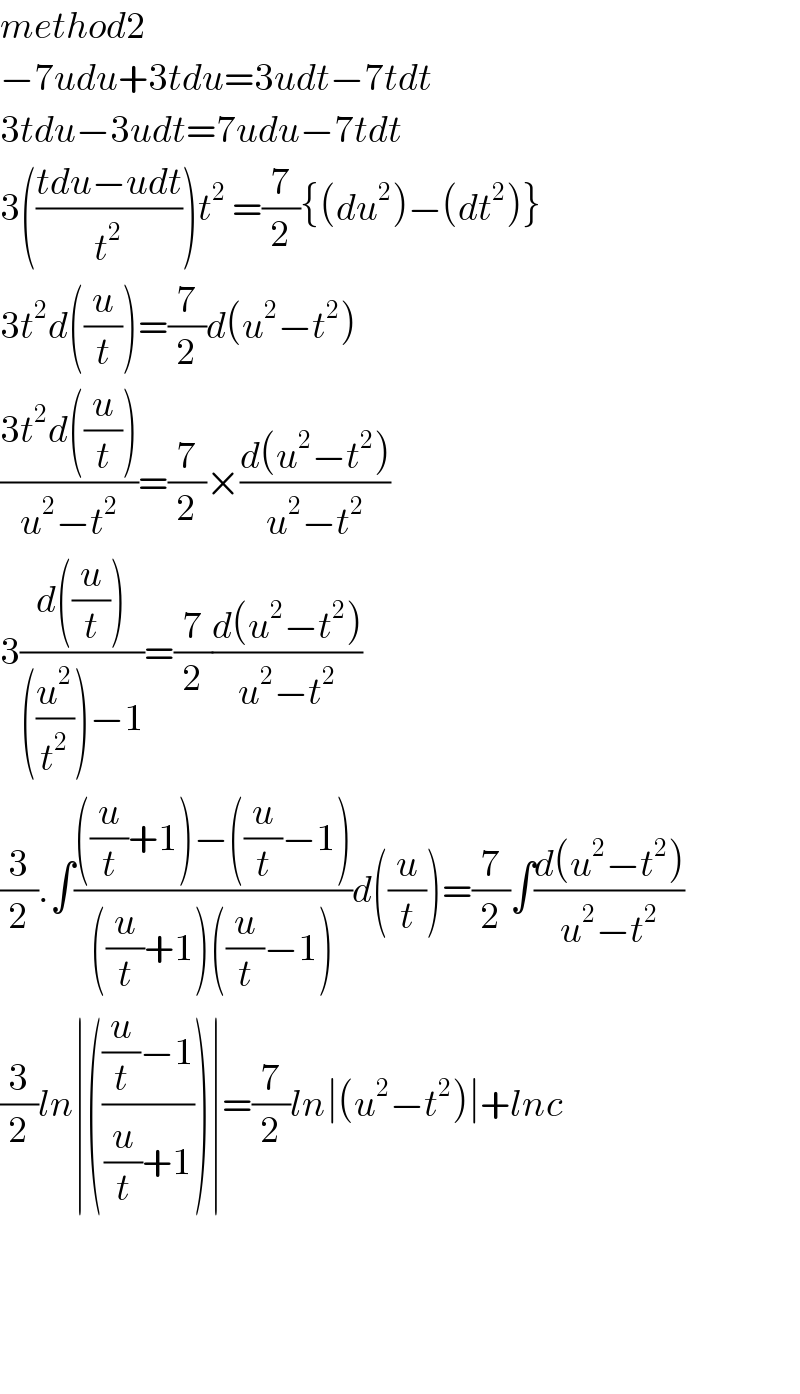
$${method}\mathrm{2} \\ $$$$−\mathrm{7}{udu}+\mathrm{3}{tdu}=\mathrm{3}{udt}−\mathrm{7}{tdt} \\ $$$$\mathrm{3}{tdu}−\mathrm{3}{udt}=\mathrm{7}{udu}−\mathrm{7}{tdt} \\ $$$$\mathrm{3}\left(\frac{{tdu}−{udt}}{{t}^{\mathrm{2}} }\right){t}^{\mathrm{2}} \:=\frac{\mathrm{7}}{\mathrm{2}}\left\{\left({du}^{\mathrm{2}} \right)−\left({dt}^{\mathrm{2}} \right)\right\} \\ $$$$\mathrm{3}{t}^{\mathrm{2}} {d}\left(\frac{{u}}{{t}}\right)=\frac{\mathrm{7}}{\mathrm{2}}{d}\left({u}^{\mathrm{2}} −{t}^{\mathrm{2}} \right) \\ $$$$\frac{\mathrm{3}{t}^{\mathrm{2}} {d}\left(\frac{{u}}{{t}}\right)}{{u}^{\mathrm{2}} −{t}^{\mathrm{2}} }=\frac{\mathrm{7}}{\mathrm{2}}×\frac{{d}\left({u}^{\mathrm{2}} −{t}^{\mathrm{2}} \right)}{{u}^{\mathrm{2}} −{t}^{\mathrm{2}} } \\ $$$$\mathrm{3}\frac{{d}\left(\frac{{u}}{{t}}\right)}{\left(\frac{{u}^{\mathrm{2}} }{{t}^{\mathrm{2}} }\right)−\mathrm{1}}=\frac{\mathrm{7}}{\mathrm{2}}\frac{{d}\left({u}^{\mathrm{2}} −{t}^{\mathrm{2}} \right)}{{u}^{\mathrm{2}} −{t}^{\mathrm{2}} } \\ $$$$\frac{\mathrm{3}}{\mathrm{2}}.\int\frac{\left(\frac{{u}}{{t}}+\mathrm{1}\right)−\left(\frac{{u}}{{t}}−\mathrm{1}\right)}{\left(\frac{{u}}{{t}}+\mathrm{1}\right)\left(\frac{{u}}{{t}}−\mathrm{1}\right)}{d}\left(\frac{{u}}{{t}}\right)=\frac{\mathrm{7}}{\mathrm{2}}\int\frac{{d}\left({u}^{\mathrm{2}} −{t}^{\mathrm{2}} \right)}{{u}^{\mathrm{2}} −{t}^{\mathrm{2}} } \\ $$$$\frac{\mathrm{3}}{\mathrm{2}}{ln}\mid\left(\frac{\frac{{u}}{{t}}−\mathrm{1}}{\frac{{u}}{{t}}+\mathrm{1}}\right)\mid=\frac{\mathrm{7}}{\mathrm{2}}{ln}\mid\left({u}^{\mathrm{2}} −{t}^{\mathrm{2}} \right)\mid+{lnc} \\ $$$$ \\ $$$$ \\ $$$$ \\ $$
Commented by rahul 19 last updated on 17/Aug/18
thanks sir��
Commented by tanmay.chaudhury50@gmail.com last updated on 17/Aug/18

$${its}\:{ok}... \\ $$
Commented by tanmay.chaudhury50@gmail.com last updated on 17/Aug/18
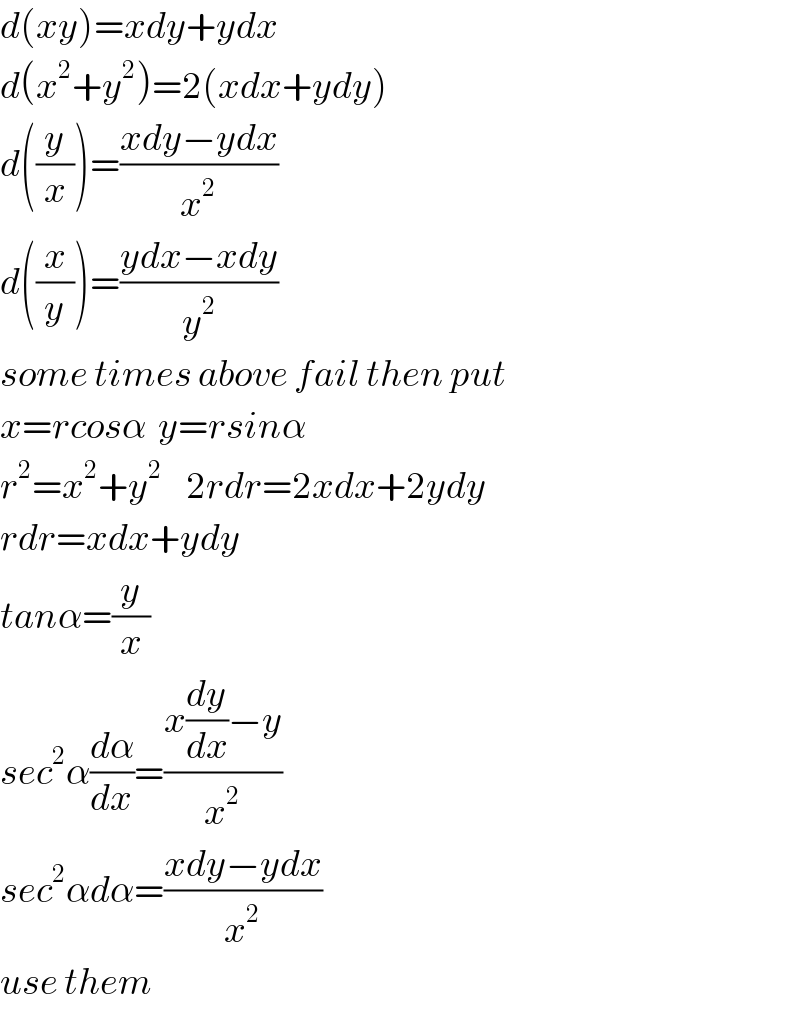
$${d}\left({xy}\right)={xdy}+{ydx} \\ $$$${d}\left({x}^{\mathrm{2}} +{y}^{\mathrm{2}} \right)=\mathrm{2}\left({xdx}+{ydy}\right) \\ $$$${d}\left(\frac{{y}}{{x}}\right)=\frac{{xdy}−{ydx}}{{x}^{\mathrm{2}} } \\ $$$${d}\left(\frac{{x}}{{y}}\right)=\frac{{ydx}−{xdy}}{{y}^{\mathrm{2}} } \\ $$$${some}\:{times}\:{above}\:{fail}\:{then}\:{put} \\ $$$${x}={rcos}\alpha\:\:{y}={rsin}\alpha \\ $$$${r}^{\mathrm{2}} ={x}^{\mathrm{2}} +{y}^{\mathrm{2}} \:\:\:\:\mathrm{2}{rdr}=\mathrm{2}{xdx}+\mathrm{2}{ydy} \\ $$$${rdr}={xdx}+{ydy} \\ $$$${tan}\alpha=\frac{{y}}{{x}} \\ $$$${sec}^{\mathrm{2}} \alpha\frac{{d}\alpha}{{dx}}=\frac{{x}\frac{{dy}}{{dx}}−{y}}{{x}^{\mathrm{2}} } \\ $$$${sec}^{\mathrm{2}} \alpha{d}\alpha=\frac{{xdy}−{ydx}}{{x}^{\mathrm{2}} } \\ $$$${use}\:{them}\: \\ $$
Commented by rahul 19 last updated on 17/Aug/18

$$\mathrm{Sir},\:\mathrm{don}'\mathrm{t}\:\mathrm{you}\:\mathrm{feel}\:\mathrm{quite}\:\mathrm{bad}\:\mathrm{when} \\ $$$$\mathrm{you}\:\mathrm{came}\:\mathrm{to}\:\mathrm{know}\:\mathrm{our}\:\mathrm{beloved}\:\mathrm{Atalji} \\ $$$$\mathrm{is}\:\mathrm{no}\:\mathrm{more}\:\mathrm{with}\:\mathrm{us}. \\ $$
Commented by tanmay.chaudhury50@gmail.com last updated on 17/Aug/18

$${yes}...{he}\:{was}\:{a}\:{true}\:{mass}\:{leader}...{good}\:{orator}.. \\ $$$${excellent}\:{writer}...{above}\:{all}\:{true}\:{replica}\:{of}\:{human} \\ $$$${being}... \\ $$
