
Question Number 11854 by tawa last updated on 02/Apr/17
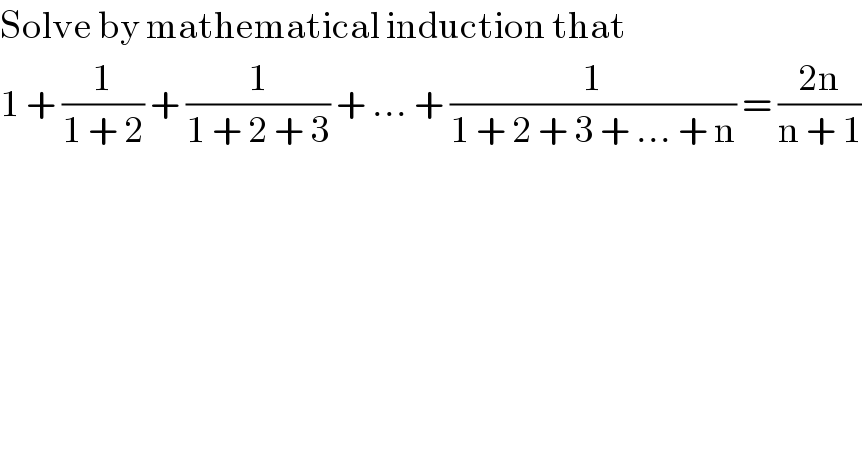
$$\mathrm{Solve}\:\mathrm{by}\:\mathrm{mathematical}\:\mathrm{induction}\:\mathrm{that} \\ $$$$\mathrm{1}\:+\:\frac{\mathrm{1}}{\mathrm{1}\:+\:\mathrm{2}}\:+\:\frac{\mathrm{1}}{\mathrm{1}\:+\:\mathrm{2}\:+\:\mathrm{3}}\:+\:...\:+\:\frac{\mathrm{1}}{\mathrm{1}\:+\:\mathrm{2}\:+\:\mathrm{3}\:+\:...\:+\:\mathrm{n}}\:=\:\frac{\mathrm{2n}}{\mathrm{n}\:+\:\mathrm{1}} \\ $$
Answered by sandy_suhendra last updated on 03/Apr/17
![for n=1 1=((2.1)/(1+1)) (is true) for n=k 1+(1/(1+2))+...+(1/(1+2+3+...+k))=((2k)/(k+1)) for n=(k+1) should be = ((2(k+1))/([(k+1)+1])) [1+(1/(1+2))+...+(1/(1+2+3...+k))]+(1/(1+2+3+...+k+(k+1))) =((2k)/(k+1)) + (1/(((k+1)/2)(1+k+1))) =((2k)/(k+1))+(2/((k+1)(k+2))) =((2k(k+2)+2)/((k+1)(k+2))) =((2k^2 +4k+2)/((k+1)(k+2))) =((2(k+1)(k+1))/((k+1)[(k+1)+1])) =((2(k+1))/([(k+1)+1])) (is proved)](Q11857.png)
$$\mathrm{for}\:\mathrm{n}=\mathrm{1} \\ $$$$\mathrm{1}=\frac{\mathrm{2}.\mathrm{1}}{\mathrm{1}+\mathrm{1}}\:\left(\mathrm{is}\:\mathrm{true}\right) \\ $$$$ \\ $$$$\mathrm{for}\:\mathrm{n}=\mathrm{k} \\ $$$$\mathrm{1}+\frac{\mathrm{1}}{\mathrm{1}+\mathrm{2}}+...+\frac{\mathrm{1}}{\mathrm{1}+\mathrm{2}+\mathrm{3}+...+\mathrm{k}}=\frac{\mathrm{2k}}{\mathrm{k}+\mathrm{1}} \\ $$$$ \\ $$$$\mathrm{for}\:\mathrm{n}=\left(\mathrm{k}+\mathrm{1}\right)\:\mathrm{should}\:\mathrm{be}\:=\:\frac{\mathrm{2}\left(\mathrm{k}+\mathrm{1}\right)}{\left[\left(\mathrm{k}+\mathrm{1}\right)+\mathrm{1}\right]}\:\:\:\:\: \\ $$$$\left[\mathrm{1}+\frac{\mathrm{1}}{\mathrm{1}+\mathrm{2}}+...+\frac{\mathrm{1}}{\mathrm{1}+\mathrm{2}+\mathrm{3}...+\mathrm{k}}\right]+\frac{\mathrm{1}}{\mathrm{1}+\mathrm{2}+\mathrm{3}+...+\mathrm{k}+\left(\mathrm{k}+\mathrm{1}\right)}\:\:\:\:\: \\ $$$$=\frac{\mathrm{2k}}{\mathrm{k}+\mathrm{1}}\:+\:\frac{\mathrm{1}}{\frac{\mathrm{k}+\mathrm{1}}{\mathrm{2}}\left(\mathrm{1}+\mathrm{k}+\mathrm{1}\right)} \\ $$$$=\frac{\mathrm{2k}}{\mathrm{k}+\mathrm{1}}+\frac{\mathrm{2}}{\left(\mathrm{k}+\mathrm{1}\right)\left(\mathrm{k}+\mathrm{2}\right)} \\ $$$$=\frac{\mathrm{2k}\left(\mathrm{k}+\mathrm{2}\right)+\mathrm{2}}{\left(\mathrm{k}+\mathrm{1}\right)\left(\mathrm{k}+\mathrm{2}\right)} \\ $$$$=\frac{\mathrm{2k}^{\mathrm{2}} +\mathrm{4k}+\mathrm{2}}{\left(\mathrm{k}+\mathrm{1}\right)\left(\mathrm{k}+\mathrm{2}\right)} \\ $$$$=\frac{\mathrm{2}\left(\mathrm{k}+\mathrm{1}\right)\left(\mathrm{k}+\mathrm{1}\right)}{\left(\mathrm{k}+\mathrm{1}\right)\left[\left(\mathrm{k}+\mathrm{1}\right)+\mathrm{1}\right]} \\ $$$$=\frac{\mathrm{2}\left(\mathrm{k}+\mathrm{1}\right)}{\left[\left(\mathrm{k}+\mathrm{1}\right)+\mathrm{1}\right]}\:\:\:\:\:\left(\mathrm{is}\:\mathrm{proved}\right) \\ $$
Commented by Mr Chheang Chantria last updated on 03/Apr/17
$$\boldsymbol{{perfect}}\:\boldsymbol{{solution}}. \\ $$
Commented by tawa last updated on 03/Apr/17

$$\mathrm{God}\:\mathrm{bless}\:\mathrm{you}\:\mathrm{sir}. \\ $$
