
Question Number 193676 by lapache last updated on 18/Jun/23
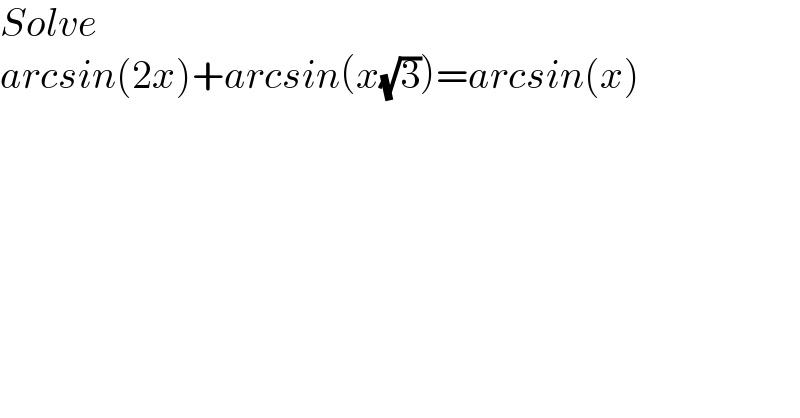
$${Solve} \\ $$$${arcsin}\left(\mathrm{2}{x}\right)+{arcsin}\left({x}\sqrt{\mathrm{3}}\right)={arcsin}\left({x}\right) \\ $$
Answered by Frix last updated on 18/Jun/23
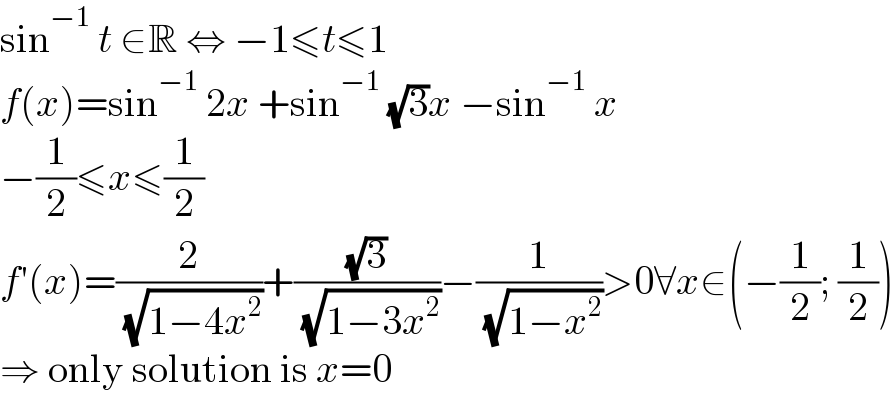
$$\mathrm{sin}^{−\mathrm{1}} \:{t}\:\in\mathbb{R}\:\Leftrightarrow\:−\mathrm{1}\leqslant{t}\leqslant\mathrm{1} \\ $$$${f}\left({x}\right)=\mathrm{sin}^{−\mathrm{1}} \:\mathrm{2}{x}\:+\mathrm{sin}^{−\mathrm{1}} \:\sqrt{\mathrm{3}}{x}\:−\mathrm{sin}^{−\mathrm{1}} \:{x} \\ $$$$−\frac{\mathrm{1}}{\mathrm{2}}\leqslant{x}\leqslant\frac{\mathrm{1}}{\mathrm{2}} \\ $$$${f}'\left({x}\right)=\frac{\mathrm{2}}{\:\sqrt{\mathrm{1}−\mathrm{4}{x}^{\mathrm{2}} }}+\frac{\sqrt{\mathrm{3}}}{\:\sqrt{\mathrm{1}−\mathrm{3}{x}^{\mathrm{2}} }}−\frac{\mathrm{1}}{\:\sqrt{\mathrm{1}−{x}^{\mathrm{2}} }}>\mathrm{0}\forall{x}\in\left(−\frac{\mathrm{1}}{\mathrm{2}};\:\frac{\mathrm{1}}{\mathrm{2}}\right) \\ $$$$\Rightarrow\:\mathrm{only}\:\mathrm{solution}\:\mathrm{is}\:{x}=\mathrm{0} \\ $$
