
Question Number 103503 by 175mohamed last updated on 15/Jul/20
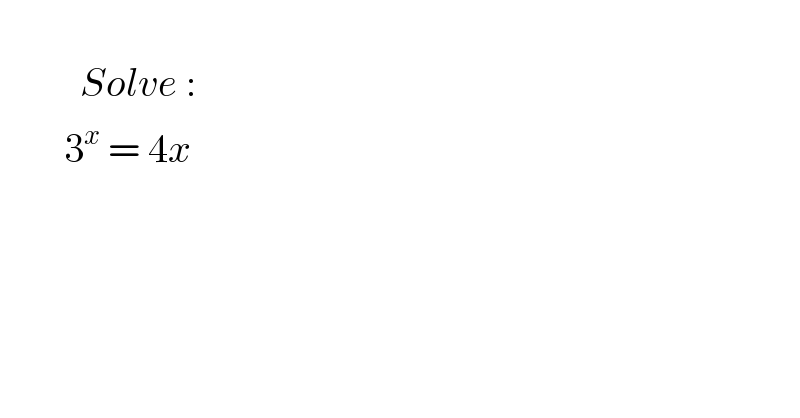
$$\:\:\: \\ $$$$\:\:\:\:\:\:\:\:\:\:{Solve}\:: \\ $$$$\:\:\:\:\:\:\:\:\mathrm{3}^{{x}} \:=\:\mathrm{4}{x} \\ $$
Answered by Dwaipayan Shikari last updated on 15/Jul/20
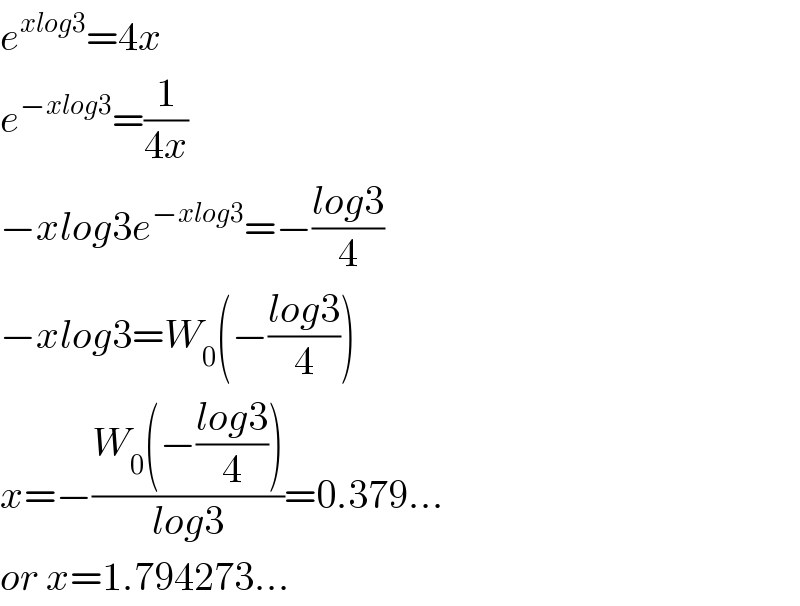
$${e}^{{xlog}\mathrm{3}} =\mathrm{4}{x} \\ $$$${e}^{−{xlog}\mathrm{3}} =\frac{\mathrm{1}}{\mathrm{4}{x}} \\ $$$$−{xlog}\mathrm{3}{e}^{−{xlog}\mathrm{3}} =−\frac{{log}\mathrm{3}}{\mathrm{4}} \\ $$$$−{xlog}\mathrm{3}={W}_{\mathrm{0}} \left(−\frac{{log}\mathrm{3}}{\mathrm{4}}\right) \\ $$$${x}=−\frac{{W}_{\mathrm{0}} \left(−\frac{{log}\mathrm{3}}{\mathrm{4}}\right)}{{log}\mathrm{3}}=\mathrm{0}.\mathrm{379}... \\ $$$${or}\:{x}=\mathrm{1}.\mathrm{794273}... \\ $$
Commented by mr W last updated on 15/Jul/20
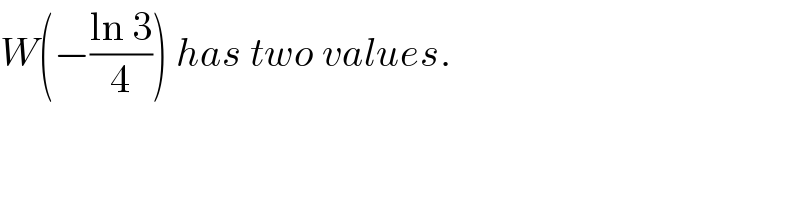
$${W}\left(−\frac{\mathrm{ln}\:\mathrm{3}}{\mathrm{4}}\right)\:{has}\:{two}\:{values}. \\ $$
Answered by OlafThorendsen last updated on 15/Jul/20
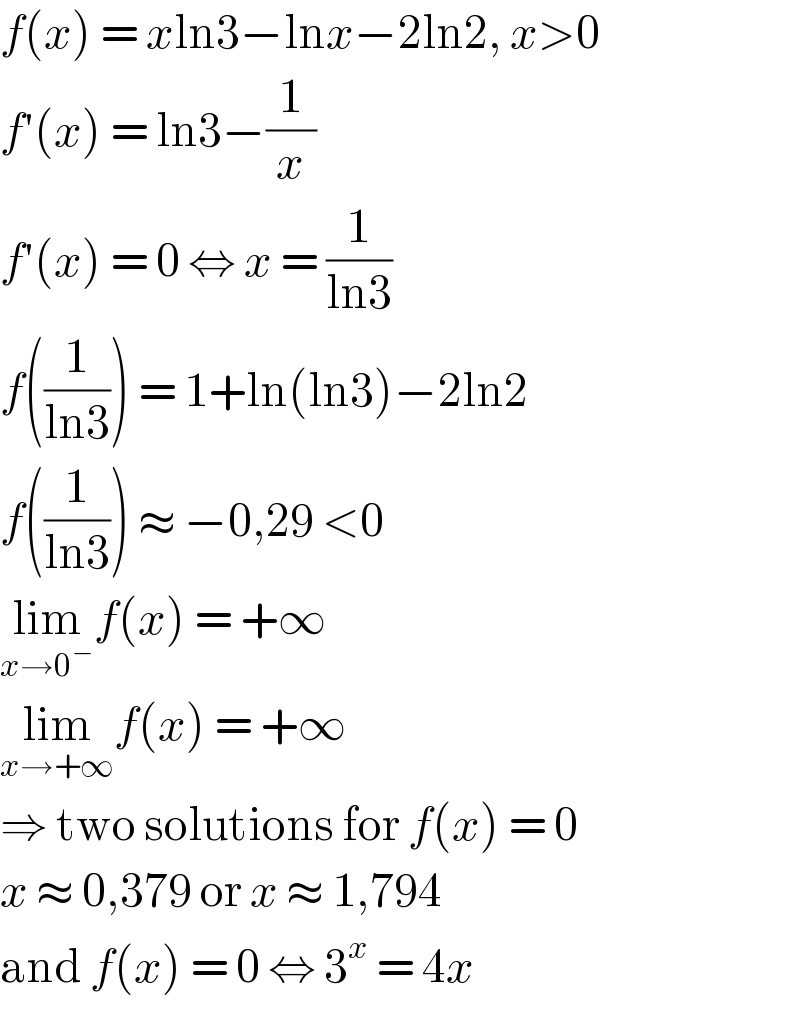
$${f}\left({x}\right)\:=\:{x}\mathrm{ln3}−\mathrm{ln}{x}−\mathrm{2ln2},\:{x}>\mathrm{0} \\ $$$${f}'\left({x}\right)\:=\:\mathrm{ln3}−\frac{\mathrm{1}}{{x}} \\ $$$${f}'\left({x}\right)\:=\:\mathrm{0}\:\Leftrightarrow\:{x}\:=\:\frac{\mathrm{1}}{\mathrm{ln3}} \\ $$$${f}\left(\frac{\mathrm{1}}{\mathrm{ln3}}\right)\:=\:\mathrm{1}+\mathrm{ln}\left(\mathrm{ln3}\right)−\mathrm{2ln2} \\ $$$${f}\left(\frac{\mathrm{1}}{\mathrm{ln3}}\right)\:\approx\:−\mathrm{0},\mathrm{29}\:<\mathrm{0} \\ $$$$\underset{{x}\rightarrow\mathrm{0}^{−} } {\mathrm{lim}}{f}\left({x}\right)\:=\:+\infty \\ $$$$\underset{{x}\rightarrow+\infty} {\mathrm{lim}}{f}\left({x}\right)\:=\:+\infty \\ $$$$\Rightarrow\:\mathrm{two}\:\mathrm{solutions}\:\mathrm{for}\:{f}\left({x}\right)\:=\:\mathrm{0} \\ $$$${x}\:\approx\:\mathrm{0},\mathrm{379}\:\mathrm{or}\:{x}\:\approx\:\mathrm{1},\mathrm{794} \\ $$$$\mathrm{and}\:{f}\left({x}\right)\:=\:\mathrm{0}\:\Leftrightarrow\:\mathrm{3}^{{x}} \:=\:\mathrm{4}{x} \\ $$
