Question and Answers Forum

All Questions      Topic List

Algebra Questions

Previous in All Question      Next in All Question      

Previous in Algebra      Next in Algebra      

Question Number 217940 by ArshadS last updated on 23/Mar/25

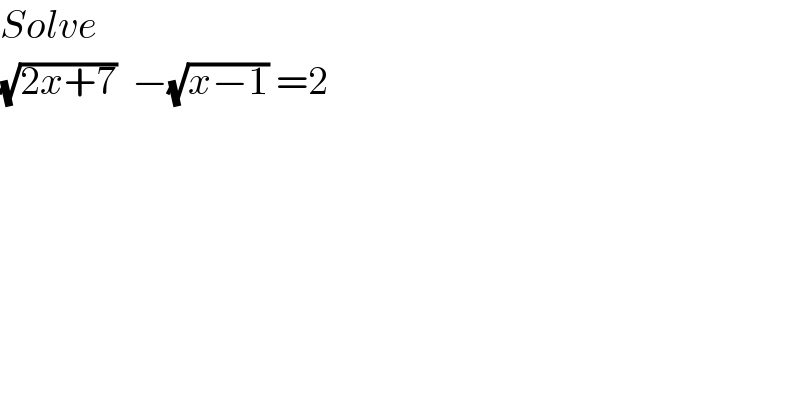
Solve (√(2x+7)) −(√(x−1)) =2

$${Solve} \\ $$$$\sqrt{\mathrm{2}{x}+\mathrm{7}}\:\:−\sqrt{{x}−\mathrm{1}}\:=\mathrm{2}\:\:\:\:\:\:\:\:\:\:\: \\ $$

Answered by Frix last updated on 23/Mar/25

No real solution because min (lhs) >2 a, b ∈R∧b≠0 (√(2x+7))=a+2+bi ⇒ x=((a^2 −b^2 +4a−3)/2)+(a+2)bi (√(x−1))=a+bi ⇒ x=a^2 −b^2 +1+2abi ⇒ { ((a^2 −b^2 +4a−3=2(a^2 −b^2 +1))),(((a+2)b=2ab)) :} { ((a^2 −b^2 −4a+5=0)),((a=2 [b≠0])) :} { ((b=±1)),((a=2)) :} ⇒ x=4±4i

$$\mathrm{No}\:\mathrm{real}\:\mathrm{solution}\:\mathrm{because}\:\mathrm{min}\:\left(\mathrm{lhs}\right)\:>\mathrm{2} \\ $$$${a},\:{b}\:\in\mathbb{R}\wedge{b}\neq\mathrm{0} \\ $$$$\sqrt{\mathrm{2}{x}+\mathrm{7}}={a}+\mathrm{2}+{b}\mathrm{i}\:\Rightarrow\:{x}=\frac{{a}^{\mathrm{2}} −{b}^{\mathrm{2}} +\mathrm{4}{a}−\mathrm{3}}{\mathrm{2}}+\left({a}+\mathrm{2}\right){b}\mathrm{i} \\ $$$$\sqrt{{x}−\mathrm{1}}={a}+{b}\mathrm{i}\:\Rightarrow\:{x}={a}^{\mathrm{2}} −{b}^{\mathrm{2}} +\mathrm{1}+\mathrm{2a}{b}\mathrm{i} \\ $$$$\Rightarrow \\ $$$$\begin{cases}{{a}^{\mathrm{2}} −{b}^{\mathrm{2}} +\mathrm{4}{a}−\mathrm{3}=\mathrm{2}\left({a}^{\mathrm{2}} −{b}^{\mathrm{2}} +\mathrm{1}\right)}\\{\left({a}+\mathrm{2}\right){b}=\mathrm{2}{ab}}\end{cases} \\ $$$$\begin{cases}{{a}^{\mathrm{2}} −{b}^{\mathrm{2}} −\mathrm{4}{a}+\mathrm{5}=\mathrm{0}}\\{{a}=\mathrm{2}\:\:\:\:\:\left[{b}\neq\mathrm{0}\right]}\end{cases} \\ $$$$\begin{cases}{{b}=\pm\mathrm{1}}\\{{a}=\mathrm{2}}\end{cases} \\ $$$$\Rightarrow\:{x}=\mathrm{4}\pm\mathrm{4i} \\ $$

Answered by mehdee7396 last updated on 23/Mar/25

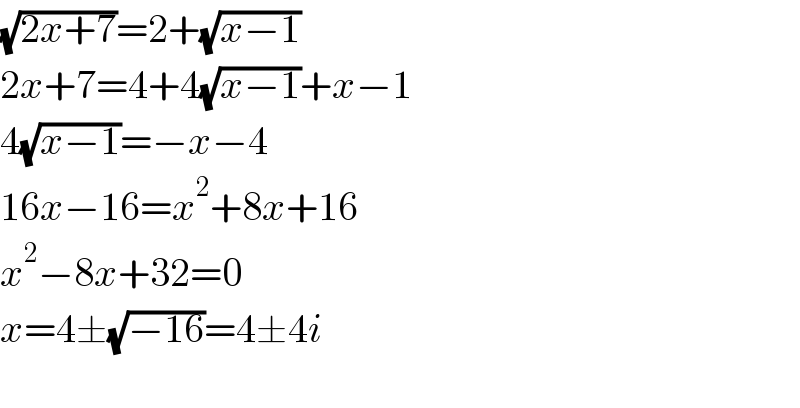
(√(2x+7))=2+(√(x−1)) 2x+7=4+4(√(x−1))+x−1 4(√(x−1))=−x−4 16x−16=x^2 +8x+16 x^2 −8x+32=0 x=4±(√(−16))=4±4i

$$\sqrt{\mathrm{2}{x}+\mathrm{7}}=\mathrm{2}+\sqrt{{x}−\mathrm{1}} \\ $$$$\mathrm{2}{x}+\mathrm{7}=\mathrm{4}+\mathrm{4}\sqrt{{x}−\mathrm{1}}+{x}−\mathrm{1} \\ $$$$\mathrm{4}\sqrt{{x}−\mathrm{1}}=−{x}−\mathrm{4} \\ $$$$\mathrm{16}{x}−\mathrm{16}={x}^{\mathrm{2}} +\mathrm{8}{x}+\mathrm{16} \\ $$$${x}^{\mathrm{2}} −\mathrm{8}{x}+\mathrm{32}=\mathrm{0} \\ $$$${x}=\mathrm{4}\pm\sqrt{−\mathrm{16}}=\mathrm{4}\pm\mathrm{4}{i} \\ $$$$ \\ $$

Answered by Rasheed.Sindhi last updated on 24/Mar/25

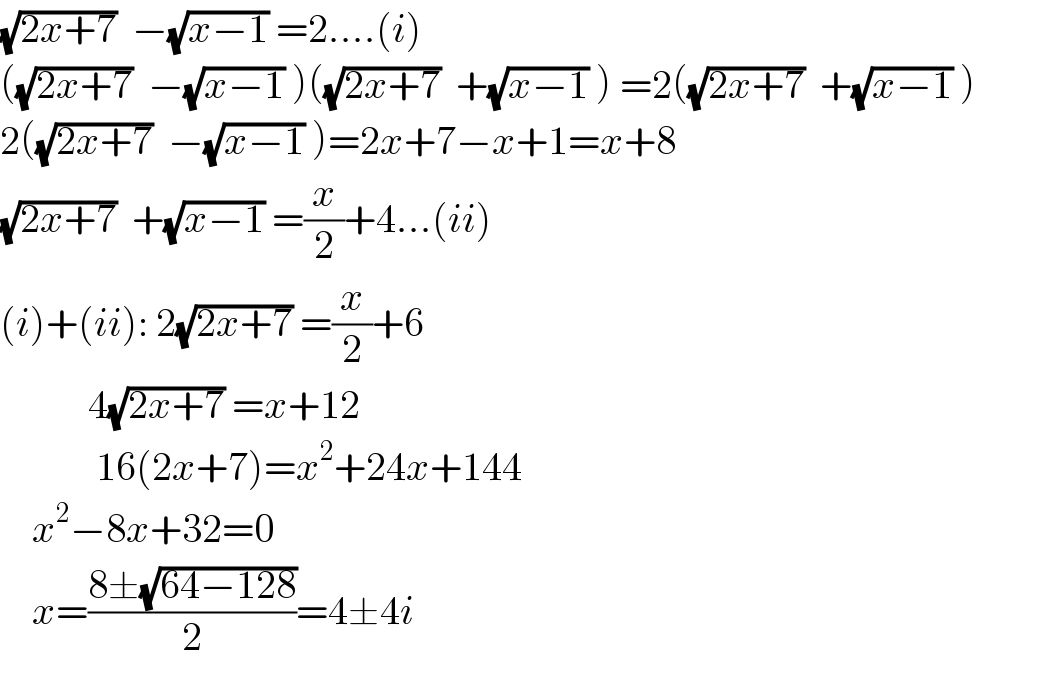
(√(2x+7)) −(√(x−1)) =2....(i) ((√(2x+7)) −(√(x−1)) )((√(2x+7)) +(√(x−1)) ) =2((√(2x+7)) +(√(x−1)) ) 2((√(2x+7)) −(√(x−1)) )=2x+7−x+1=x+8 (√(2x+7)) +(√(x−1)) =(x/2)+4...(ii) (i)+(ii): 2(√(2x+7)) =(x/2)+6 4(√(2x+7)) =x+12 16(2x+7)=x^2 +24x+144 x^2 −8x+32=0 x=((8±(√(64−128)))/2)=4±4i

$$\sqrt{\mathrm{2}{x}+\mathrm{7}}\:\:−\sqrt{{x}−\mathrm{1}}\:=\mathrm{2}....\left({i}\right)\:\:\:\:\:\:\:\:\:\:\: \\ $$$$\left(\sqrt{\mathrm{2}{x}+\mathrm{7}}\:\:−\sqrt{{x}−\mathrm{1}}\:\right)\left(\sqrt{\mathrm{2}{x}+\mathrm{7}}\:\:+\sqrt{{x}−\mathrm{1}}\:\right)\:=\mathrm{2}\left(\sqrt{\mathrm{2}{x}+\mathrm{7}}\:\:+\sqrt{{x}−\mathrm{1}}\:\right)\:\:\:\:\:\:\:\:\:\:\: \\ $$$$\mathrm{2}\left(\sqrt{\mathrm{2}{x}+\mathrm{7}}\:\:−\sqrt{{x}−\mathrm{1}}\:\right)=\mathrm{2}{x}+\mathrm{7}−{x}+\mathrm{1}={x}+\mathrm{8} \\ $$$$\sqrt{\mathrm{2}{x}+\mathrm{7}}\:\:+\sqrt{{x}−\mathrm{1}}\:=\frac{{x}}{\mathrm{2}}+\mathrm{4}...\left({ii}\right) \\ $$$$\left({i}\right)+\left({ii}\right):\:\mathrm{2}\sqrt{\mathrm{2}{x}+\mathrm{7}}\:=\frac{{x}}{\mathrm{2}}+\mathrm{6} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\mathrm{4}\sqrt{\mathrm{2}{x}+\mathrm{7}}\:={x}+\mathrm{12} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\mathrm{16}\left(\mathrm{2}{x}+\mathrm{7}\right)={x}^{\mathrm{2}} +\mathrm{24}{x}+\mathrm{144} \\ $$$$\:\:\:\:{x}^{\mathrm{2}} −\mathrm{8}{x}+\mathrm{32}=\mathrm{0} \\ $$$$\:\:\:\:{x}=\frac{\mathrm{8}\pm\sqrt{\mathrm{64}−\mathrm{128}}}{\mathrm{2}}=\mathrm{4}\pm\mathrm{4}{i} \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com