
Question Number 850 by sagarwal last updated on 25/Mar/15

$$\mathrm{Solve}\:\mid\mathrm{2}{x}+\mathrm{4}\mid\geqslant\mathrm{14} \\ $$
Answered by 123456 last updated on 25/Mar/15
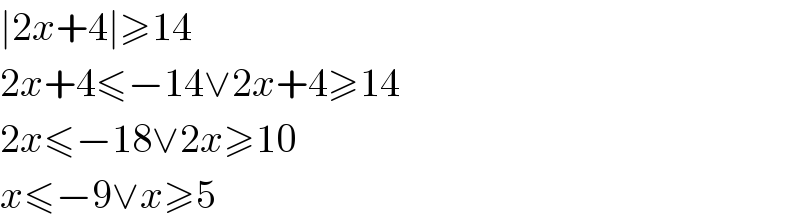
$$\mid\mathrm{2}{x}+\mathrm{4}\mid\geqslant\mathrm{14} \\ $$$$\mathrm{2}{x}+\mathrm{4}\leqslant−\mathrm{14}\vee\mathrm{2}{x}+\mathrm{4}\geqslant\mathrm{14} \\ $$$$\mathrm{2}{x}\leqslant−\mathrm{18}\vee\mathrm{2}{x}\geqslant\mathrm{10} \\ $$$${x}\leqslant−\mathrm{9}\vee{x}\geqslant\mathrm{5} \\ $$
Commented by sagarwal last updated on 26/Mar/15

$$\mathrm{Thanks} \\ $$
Answered by malwaan last updated on 25/Mar/15
![2x+4=0 ⇒x=−2 x≥−2⇒2x+4≥14⇒x≥5 x<−2⇒−2x−4≥14 ⇒2x+4≤−14⇒x≤−9 ∴solution set =R/]−9 . 5[ OR =]−∞ . −9]∪[5 . ∞[](Q853.png)
$$\mathrm{2}{x}+\mathrm{4}=\mathrm{0}\:\Rightarrow{x}=−\mathrm{2} \\ $$$${x}\geqslant−\mathrm{2}\Rightarrow\mathrm{2}{x}+\mathrm{4}\geqslant\mathrm{14}\Rightarrow{x}\geqslant\mathrm{5} \\ $$$${x}<−\mathrm{2}\Rightarrow−\mathrm{2}{x}−\mathrm{4}\geqslant\mathrm{14} \\ $$$$\Rightarrow\mathrm{2}{x}+\mathrm{4}\leqslant−\mathrm{14}\Rightarrow{x}\leqslant−\mathrm{9} \\ $$$$\left.\therefore{solution}\:{set}\:={R}/\right]−\mathrm{9}\:.\:\mathrm{5}\left[\:\right. \\ $$$$\left.{O}\left.{R}\:=\right]−\infty\:.\:−\mathrm{9}\right]\cup\left[\mathrm{5}\:.\:\infty\left[\right.\right. \\ $$
Commented by sagarwal last updated on 26/Mar/15

$$\mathrm{Thanls} \\ $$
