
Question Number 42908 by naka3546 last updated on 04/Sep/18
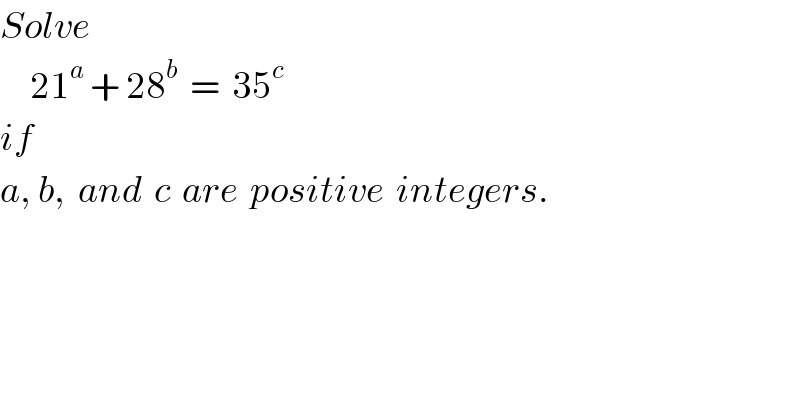
$${Solve}\: \\ $$$$\:\:\:\:\:\mathrm{21}^{{a}} \:+\:\mathrm{28}^{{b}} \:\:=\:\:\mathrm{35}^{{c}} \\ $$$${if} \\ $$$${a},\:{b},\:\:{and}\:\:{c}\:\:{are}\:\:{positive}\:\:{integers}. \\ $$
Answered by tanmay.chaudhury50@gmail.com last updated on 04/Sep/18
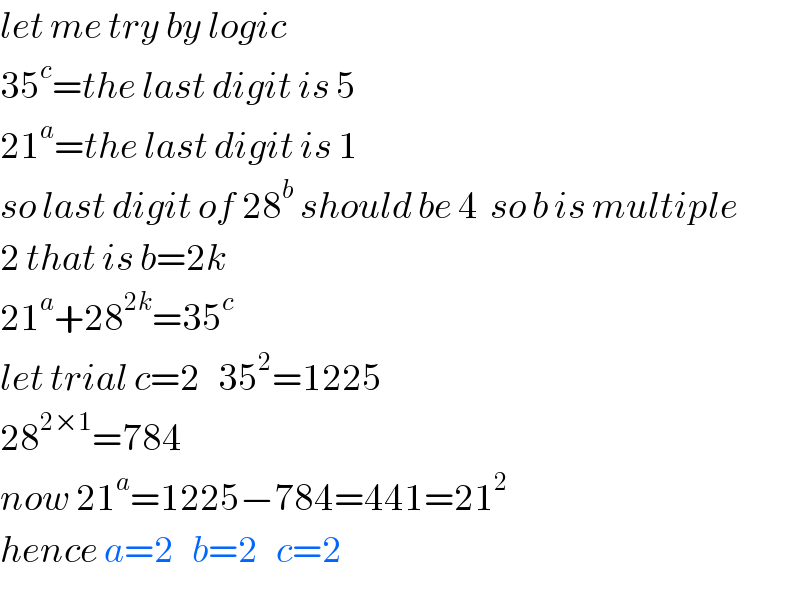
$${let}\:{me}\:{try}\:{by}\:{logic} \\ $$$$\mathrm{35}^{{c}} ={the}\:{last}\:{digit}\:{is}\:\mathrm{5} \\ $$$$\mathrm{21}^{{a}} ={the}\:{last}\:{digit}\:{is}\:\mathrm{1} \\ $$$${so}\:{last}\:{digit}\:{of}\:\mathrm{28}^{{b}} \:{should}\:{be}\:\mathrm{4}\:\:{so}\:{b}\:{is}\:{multiple}\: \\ $$$$\mathrm{2}\:{that}\:{is}\:{b}=\mathrm{2}{k} \\ $$$$\mathrm{21}^{{a}} +\mathrm{28}^{\mathrm{2}{k}} =\mathrm{35}^{{c}} \\ $$$${let}\:{trial}\:{c}=\mathrm{2}\:\:\:\mathrm{35}^{\mathrm{2}} =\mathrm{1225} \\ $$$$\mathrm{28}^{\mathrm{2}×\mathrm{1}} =\mathrm{784}\:\:\: \\ $$$${now}\:\mathrm{21}^{{a}} =\mathrm{1225}−\mathrm{784}=\mathrm{441}=\mathrm{21}^{\mathrm{2}} \\ $$$${hence}\:{a}=\mathrm{2}\:\:\:{b}=\mathrm{2}\:\:\:{c}=\mathrm{2} \\ $$
Commented by MJS last updated on 04/Sep/18
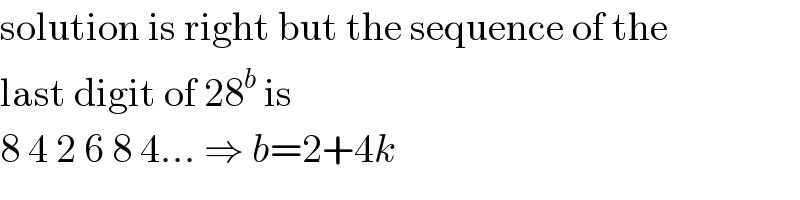
$$\mathrm{solution}\:\mathrm{is}\:\mathrm{right}\:\mathrm{but}\:\mathrm{the}\:\mathrm{sequence}\:\mathrm{of}\:\mathrm{the} \\ $$$$\mathrm{last}\:\mathrm{digit}\:\mathrm{of}\:\mathrm{28}^{{b}} \:\mathrm{is} \\ $$$$\mathrm{8}\:\mathrm{4}\:\mathrm{2}\:\mathrm{6}\:\mathrm{8}\:\mathrm{4}...\:\Rightarrow\:{b}=\mathrm{2}+\mathrm{4}{k} \\ $$
Commented by tanmay.chaudhury50@gmail.com last updated on 05/Sep/18
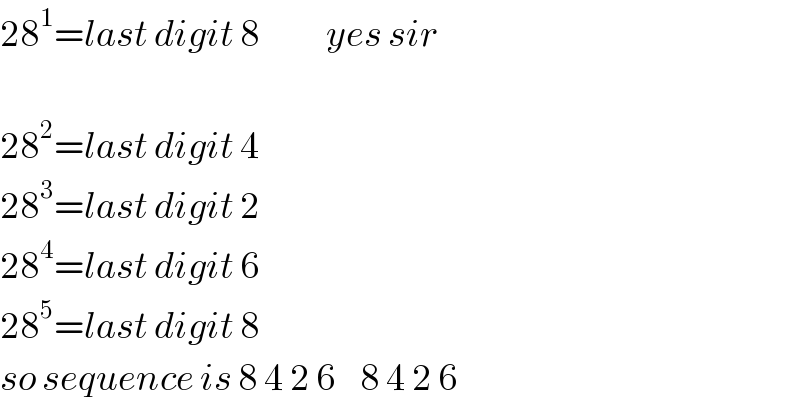
$$\mathrm{28}^{\mathrm{1}} ={last}\:{digit}\:\mathrm{8}\:\:\:\:\:\:\:\:\:\:\:{yes}\:{sir} \\ $$$$ \\ $$$$\mathrm{28}^{\mathrm{2}} ={last}\:{digit}\:\mathrm{4} \\ $$$$\mathrm{28}^{\mathrm{3}} ={last}\:{digit}\:\mathrm{2} \\ $$$$\mathrm{28}^{\mathrm{4}} ={last}\:{digit}\:\mathrm{6} \\ $$$$\mathrm{28}^{\mathrm{5}} ={last}\:{digit}\:\mathrm{8} \\ $$$${so}\:{sequence}\:{is}\:\mathrm{8}\:\mathrm{4}\:\mathrm{2}\:\mathrm{6}\:\:\:\:\mathrm{8}\:\mathrm{4}\:\mathrm{2}\:\mathrm{6} \\ $$
